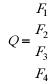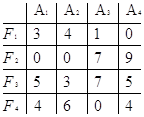|
Контрольная работа: Финансовая математикаКонтрольная работа: Финансовая математикаЗадание 1Правило торговца. Кредит в Z = 15 000 руб. выдан на N = 10 месяцев под i = 10% годовых. Договор предусматривает погашение двумя промежуточными платежами. Первая выплата в сумме R1 = 600 руб. производится через n1 = 6 месяцев, вторая выплата в сумме R2 = 9 000 руб. - через n2 = 9 месяцев. Найти выплату в конце срока кредита. Решение. Продолжительность кредита в долях года равна T =10/12=5/6. Тогда долг (кредит с процентами) составит 15 000(1 + 0,1⋅0,83) = 16 245. Интервал времени (в долях года) от момента первого платежа до окончания срока кредита t1 =(10-6) /12=1/3. Сумма первого платежа с процентами равна R1=(1+ i t1) = 600(1+0,1·1/3) =620. Остаток долга после первого платежа будет равен Z1 = 16245-620=15625. Интервал времени (в долях года) от момента второго платежа до окончания срока кредита t2 =(10-9) /12=1/12. Сумма второго платежа с процентами равна R2=(1+ i t2) =9000(1+0,1·1/12) =9075. Остаток долга будет равен Z2 = 15625-9075=6550. Отсюда следует, что в конце срока кредита погашающий платеж равен R3= 6550 руб. Таким образом, заемщиком будет выплачена сумма R1+ R2+R3= 600+9000+6550=16150 руб. При этом его долг кредитору составляет 16 245 руб. Задание 2Клиент получил ссуду Р = 200000 руб. сроком на n = 8 лет под 6% процентов годовых. Погашение кредита производится в конце каждого года равными долями. Вычислить размер ежегодного платежа и его разбиение на погашение основного долга и погашение процентов. Вычисления по формулам проверить с помощью функций ПЛТ, ОСПЛТ, ПРПЛТ. Решение. Клиент должен каждый год выплачивать банку сумму R=P∙ i/(1-(1+i) - n) =200000∙0,06/(1-(1+0,06) - 8) =32207, 19 Этот ответ можно получить, используя таблицу коэффициентов приведения a(i,k), R=P/(a(6%,8)) =200000/6, 20979=32207, 19 найдем выплаты по процентам и основного долга в конце первого года, т.е. при j = 1, Z0 = P = 200 000: D1 = i·Z0 = 0,06·200 000 = 12 000,B1 = R - D1 = 32207,19 - 12000 =20207, 19. Тогда остаток долга в конце первого года будет равен Z1 = Z0 - B1 = 200 000 - 20207,19 = 179792,81. В конце второго года, т.е. при j = 2 выплаты по процентам D2 = i·Z1 = 0,06·179792,81 ≈ 10787,57,выплаты основного долга B2 = R - D2 = 32207,19 - 10787,57 = 21419,62. Тогда остаток долга в конце второго года будет равен Z2= Z1 - B2 = 179792,81 - 21419,62 = 158373, 19. В конце третьего года, т.е. при j = 3 выплаты по процентам D3= i·Z2 = 0,06·158373,19 ≈ 9502,39, выплаты основного долга B3 = R - D3 =32207,19 -9502,39= 22704,8. Тогда остаток долга в конце третьего года будет равен Z3 = Z2 - B3 = 158373,19 - 22704,8 =135668,39. В конце четвертого года, т.е. при j = 4 выплаты по процентам D4 = i·Z3 = 0,06·135668,39 =8140,10,выплаты основного долга B4 = R - D4 =32207,19 -8140,10= 24067,08. Тогда остаток долга в конце четвертого года будет равен Z4 = Z3 - B4 = 135668,39 - 24067,08 = 111601,31. В конце пятого года, т.е. при j = 5 выплаты по процентам D5 = i·Z4 = 0,06·111601,31 =6696,08,выплаты основного долга B5 = R - D5 =32207,19 -6696,08= 25511,11. Тогда остаток долга в конце пятого года будет равен Z5 = Z4 - B5 = 111601,31 - 25511,11 = 86090,2. В конце шестого года, т.е. при j = 6 выплаты по процентам D6 = i·Z5 = 0,06·86090,2 =5165,41,выплаты основного долга B6 = R - D6 =32207,19 -5165,41= 27041,78. Тогда остаток долга в конце шестого года будет равен Z6 = Z5 - B6 = 86090,2 - 27041,78= 59048,42. В конце седьмого года, т.е. при j = 7 выплаты по процентам D7 = i·Z6 = 0,06·59048,42=3542,91,выплаты основного долга B7 = R - D7 =32207,19 -3542,91= 28664,28. Тогда остаток долга в конце седьмого года будет равен Z7 = Z6 - B7 = 59048,42 - 28664,28= 30384,14. В конце восьмого года, т.е. при j = 8 выплаты по процентам D8 = i·Z7 = 0,06·30384,14 =1823,05,выплаты основного долга B8 = R - D8 =32207,19 -1823,05= 30384,14. Тогда остаток долга в конце восьмого года будет равен Z8 = Z7 - B8 = 30384,14 - 30384,14= 0. Теперь проверим вычисления с помощью функций ПЛТ, ОСПЛТ, ПРПЛТ
Задание 3Проект рассчитан на два года и требует инвестиции в I0 = $ 15 000. В конце первого года доход составит R1= $ 7 000, а в конце второго года - R2= $ 12 000. Найти при заданной ставке приведения i=10%: 1) чистый приведенный доход NPV; 2) чистый наращенный доход NFV; 3) cрок окупаемости без учета и с учетом времени; 4) внутреннюю ставку дохода. Вычисления по формулам проверить помощью функций ЧПС и ВСД. Решение. Из формулы при n = 2, i = 10% найдем чистый приведенный доход n NPV=∑ * Rk / (1+i) k-I0 k=1 NPV=7000/1,1+12000/1,12-15000=6363,64+9917,36-15000=1281 или NPV=R1*v(10%,1) +R2*v(10%,2) - I0 =7000*0,909091+12000*0,826446-15000=6363,64+9917,36-15000=1281 Заметим, что величина $ 6363,64 соответствует современной стоимости $ 7 000, а величина инвестиции $ 9 917,36 соответствует современной стоимости $ 12 000. NFV = (1+i) 2 ·NPV = 1,12 · 1281 = 1550,01 Найдем срок окупаемости без учета времени по формуле R1+R2+…+R [nok] +R [nok] +1=I0, что приводит к уравнению 7000 + 12000x = 15 000. Отсюда дробная часть срока окупаемости x=7000/12000=0,58 Срок окупаемости равен 1 + x = 1,58. Срок окупаемости с учетом времени по формуле: v(i,1) R1+v(i,2) R2+…+v(i, [nok]) R [nok] +xv(i, [nok] +1) R [nok] +1=I0 приводит к уравнению 7000/1,1+12000/1,12x=15000; 7000*v(10%,1) +12000*v(10%,2) x=15000; 6363,64+9917,36x=15000; x=(15000-6363,64) /9917,36=0,87 Срок окупаемости с учетом времени поступления доходов равен 1,87. Внутреннюю ставку дохода по определению находим из решения уравнения относительно i. 7000/(1+i) +12000/(1+i) 2=15000 или 15000х2-7000х-12000=0 где x = 1 + i. Сокращая на 1000, получим квадратное уравнение 15x2 - 7x - 12 = 0. Положительный корень этого уравнения x1= 1,1577 Отсюда находим, что внутренняя ставка дохода IRR = x1- 1 = 1,1577 - 1 =0,1577. Вычисления по формулам проверим в Excel с помощью функций ЧПС и ВСД.
Задание 4На финансовом рынке может сложиться одна из четырех ситуаций A1, A2, A3, A4. В условиях полной неопределенности инвестор выбирает из четырех финансовых операций F1, F2, F3, F4. Доходы инвестора определяются матрицей
Определить оптимальный выбор финансовой операции по критериям Вальда и Сэвиджа. 1. Оптимальный выбор финансовой операции по критерию Вальда. Найдем наихудший исход каждой финансовой операции, т.е. определим наименьшее число в каждой строке матрицы доходов: a1= 14, a2= 8, a3= 11, a4= 12. Согласно правилу Вальда, наибольшее среди найденных чисел определяет оптимальный доход. Следовательно, оптимальный доход равен 14, и он гарантируется выбором финансовой операции F1. 2. Оптимальный выбор финансовой операции по критерию Сэвиджа. Сначала получим из матрицы доходов матрицу рисков. Для этого в каждом столбце матрицы доходов найдем наибольшее число b1=17, b2=18, b3=18, b4=17. Вычитая из наибольшего значения столбца все его элементы, получаем столбец матрицы рисков. Следовательно, матрица рисков имеет вид Q= Найдем наихудший исход каждой финансовой операции, т.е. определим наибольший риск в каждой строке матрицы рисков: q1= 4, q2= 9, q3= 7, q4= 6. Согласно правилу Сэвиджа наименьшее среди найденных чисел определяет оптимальный доход. Следовательно, оптимальный доход равен 4, и он гарантируется выбором финансовой операции F1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |