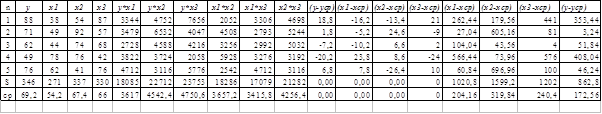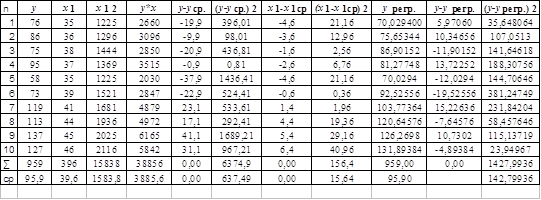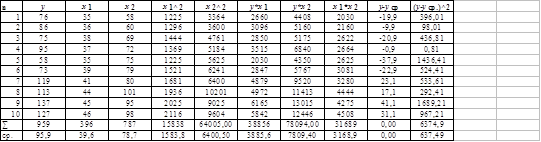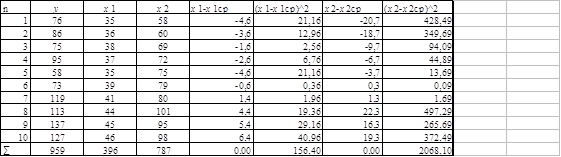|
Контрольная работа: Построение двухфакторной модели, моделей парной линейной прогрессии и множественной линейной регрессииКонтрольная работа: Построение двухфакторной модели, моделей парной линейной прогрессии и множественной линейной регрессииЗАДАНИЕ №1 По предложенной выборке наблюдений результативного признака у и факторных признаков х1,х2,х3 требуется с помощью корреляционного анализа выбрать факторные признаки для построения двухфакторной модели и пояснить свой выбор.
Решение Для получения искомых величин составим расчетную таблицу:
Получим: x1 = 54,2, х2=67,4, х3= 66; у*х1=3617; у*х2=4542,4; у*х3=4750,6; х1*х2=3657,2; х1*х3=3415,8; х2*х3= 4256,4 Рассчитаем r коэффициент корреляции между величинами у и х1; у и х2; у и х3; х1 и х2; х2 и х3; х1 и х3; Cov (x*у)= х*у –х*у Cov (x1*у)=3617-54.2*69.2 =-133,64 Cov (x2*у)=4542,4-67,4*69,2 =-121,68 Cov (x3*у)=4750,6-66*69,2 =183,4 Rх1у = cov(х1;у) = -133,64 = -133,64 =- 0,712 Var(x1)Var(y) 204,16*172,56 187,696 Rх2у = cov(х2;у)=-121,68= -121,68 = -0,5179 Var(x2)Var(y) 319,84*172,56 234,928 Rх3у = cov(х3;у)=183,4 =183,4 = 0,900 Var(x3)Var(y) 240,4*172,56 203,675 Cov (x1*x2)=x1*x2-x1*x Cov(x1*x2)=3657,2-54,2*67,4=4,12 Cov(x1*x3)=3415,8-54,2*66=-161,4 Cov(x2*x3)==4256,4-67,4*66=-192 Rх1х2 = cov(х1;х2)=4,12= 4,12 = 0,016 Var(x1)Var(х2) 204,16*319,84 255,5357 Rх1х3 = cov(х1;х3) = -161,4 = -161,4 = -0,728 Var(х1)Var(х3) 204,16*240,4 221,54 Rх2х3 = cov(х2;х3) = -192 = -192 = -0,692 Var(х2)Var(х3) 240,4*319,84 277,288 Построим расчетную таблицу для двухфакторной модели
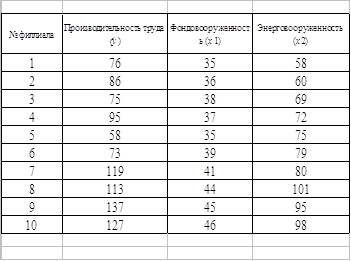
Для построения двухфакторной модели по модулю подходят х1 и х3 т.к у них более высокий показатель, но по факторному признаку х1 и х3> 0,6 значит выбираем х1 и х2 ЗАДАНИЕ № 2 Результаты обследования десяти статистически однородных филиалов фирмы в таблице (цифры условные). Требуется: А. Построить модель парной линейной прогрессии производительности труда от фактора фондовооруженности, определить коэффициент регрессии, рассчитать парный коэффициент корреляции, оценить тесноту корреляционной связи, найти коэффициент эластичности и бета – коэффициент: пояснить экономический смысл всех коэффициентов; Б. Построить модель множественной линейной регрессии производительности труда от факторов фондо- и энерго- вооруженности, найти все коэффициенты корреляции и детерминации, коэффициенты эластичности и - коэффициенты, пояснить экономический смысл всех коэффициентов.
Решение А. Обозначим производительность труда через у – резтивный признак, два других признака фондовооруженость и энерговооруженность будут фак.х1 и х2. Рассмотрим линейную модель зависимости производительности труда – у от величины фондовооруженности – х1 это модель выражения линейной функции f вида у = а0 + а1*х1, параметры которой находят в результате решения системы нормального уровня, сформированных на основе метода наименьших квадратов, суть которого заключается в то, что бы сумма квадратов отклонений фактических уравнений ряда от соответствующих, выровненных по кривой роста значений была наименьшей.
а0*_х1+а1*_х1^2=_(у*х1), где суммирование приводится по всем - n- группам, - параметры а0 и а1можно рассчитать по формуле:
var(х1) х2-2/х1 а0 = у-а1*х
396*а0+15838*а1 = 38856 Составим расчетную таблицу
Из расчета таблицы имеем ух1 = 3885,60 х1 = 1583,80 Дополнительно рассчитываем ух1 = 95,9*39,6 = 3797,64 х1 = (39,6)^2 = 1568.16 а1 = 3885,6-3797,64 = 87,96 = 5,624040 1583,8-1568,16 15,64 а0 = 95,9-5,624040*39,6 = -126,81, таким образом однофакторная модель имеет вид: у регр = а0+а1*х1 у регр = -126,812+5624041*х1 Полученное уравнение является уравнением парной регрессии, коэффициента а1 в этом уравнении называется коэффициентом регрессии. Знак этого коэффициента определяется направлением связи между у и х2. В нашем случае эта связь образуется а1 = +5,624040(+) – связь прямая.
rух1 = V1-о у регр.^ 2/ оу^2 , где оу – средняя квадратная ошибка выборки у из значений таблицы
rух1 = V1-142.79937/637.49 = 0.8809071 Чем ближе коэффициент корреляции к единице, тем теснее корреляционная связь: rух1=0,881, следовательно, связь между производительностью труда и фондовооруженностью достаточно тесная. Коэффициент детерминации rух1^2
Это означает, что фактором фондовооруженности можно объяснить 77,6% изменения производительности труда. Коэффициент эластичности Эух1 = а1*х1 ср./ у ср.; Эух1 = 5,624040*39,6/95,9
Это означает, что при увеличении фондовооруженности на 1%, производительность труда увеличится на 2,3223%. Бета коэффициент _ух1 = а1*ох1/оу, _ух1 = 5,624040*V15.64/ V637,49 = 0,8809072
Это значит, что увеличение фондовооруженности на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения производительности труда на 0,88 среднеквадратического отклонения. Б. Модуль множественных регрессий рассматривается на периметре двухфакторной линейной модели, отражающей зависимость производительности труда у, от величины фондовооруженности (х1) и энерговооруженности (х2), модуль множественной регрессии имеет вид у = а0+а1у1+а2х2. Параметры модели а0,а1,а2, находятся путем решения системы нормальных уравнений:
а0*Sх1+а1*Sх1^2+а2*S(х1*х2) = S(у*х1) а0*Sх2+а1*S(х1*х2)+а2*Sх2^2 = Sу*х2)
396*а0+15838*а1+31689*а2 = 38859 787*а0+31689*а1+64005*а2 = 78094 Рассчитаем таблицу
Решаем систему нормальным уравнением,методом Гаусса (метод исключения неизвестных). Разделим каждое уравнение системы на коэффициент при а0 соответственно:
а0+39,994949*а1+80,022727*а2 = 98,128787 а0+40,26556*а1+81,327827*а2 = 99,229987 из первогоуравнения системы вычитаем второе уравнение системы
а0 +39,994949а1+30,022727а2 = 98,128787 -0,394949-1,322727 = -2,228787 Из первого вычитаем третье уравнение:
а0+40,26556*а1+81,327827*а2 = 99,229987 -0,665563-2,627827 = -3,329987 получим систему с двумя неизвестными
0,665565*а1+2,627827а2 = 3,329987 Делим каждое уравнение на β при а1 соответственно:
а1+3,948265а2 = 5,003248 из первого вычитаем второе -0,599157а2 = 0,639979
Полученное значение а2 подставим в уравнение с двумя неизвестными: а1+3,349108а2 = 5,643227 а1 = 5,643227-3,349108*(-1,0681323) а1 = 5,643227+3,577290
Полученное значение а1 и а2 подставим в любое из уравнений с тремя неизвестными а0+39,6а+78,7а2 = 95,9 а0 = 95,9-39,6 а1-78,7 а2 а0 = 95,9-39,6*9,220517-78,7*(-1,0681323) а0 = 95,9-365,132473+84,062012 а0 = 185,170461
Получим модель: у = а0+а1х1+а2х2 у = -185,170461+9,220517х1-1,0681323х2 Ответ: у = -185,170461+9,220517х1-1,0681323х2
Парные коэффициенты корреляции: А. rух1 = ((у*х1)ср-уср*х1ср)/(оу*ох1)
Б. rух2 = ((у*х2)ср-уср*х2ср)/(оу*ох2), где ох2 = VS(х2-х2ср)^2/10
В. rх1х2 = ((х1*х2)ср-х1ср*х2ср)/(ох1*ох2)
Чем ближе коэффициент корреляции к 1, тем теснее связь. Коэффициент множественной корреляции: А. rух1х2 = V(rух1^2+rух2^2-2*rух1*rух2*rх1х2)/(1-rх1х2^2)
Таким образом, степень тесноты связи производительности труда с факторами фондовооруженности и энерговооруженности является высокой. Совокупный коэффициент детерминации:
Это означает, что совместное влияние двух факторов определяет 82,9% производительности труда. Частные коэффициенты корреляции: А. rух1(х2) = (rух1-rух2*rх1х2)/V(1-rух2^2)*(1-r х1х2^2)
т.е. теснота связи между производительностью труда и фондовооруженностью, при энерговооруженности, значительная. В. Rух2(х1) = (rух2-rух1*rх1х2)/V(1-rух1^2)*(1-r х1х2^2)
т.е. связи между производительностью труда и энерговооруженностью, при неизменной фондовооруженности, в данной выборке нет. Частные коэффициенты эластичности: А. эух1(х2) = а1*х1ср/уср
т.е. при увеличении фондовооруженности на 1% и неизменной энерговооруженности, производительность труда увеличится на 3,807%. Б. эух2(х1) = а2*х2ср/уср
т.е. при увеличении энерговооруженности, производительность труда не изменится. Частные бета β коэффициенты: А. βух1(х2) = а1*ох1/оу
это означает, что при неизменной энерговооруженности, увеличение на величину среднеквадратического отклонения размера фондовооруженности приведет к увеличению средней производительности труда на 1,444 среднеквадратического отклонения. Б. Βух2(х1) = а2*ох2/оу
это означает, что связи нет. |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |