|
Курсовая работа: Имитационное моделирование системы массового обслуживанияКурсовая работа: Имитационное моделирование системы массового обслуживанияКурсовая работа «Имитационное моделирование системы массового обслуживания» по курсу «Исследование операций» Введение При исследовании операций часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО). Каждая СМО состоит из определенного числа обслуживающих единиц (приборов, устройств, пунктов, станций), которые называются каналами обслуживания. Каналами могут быть линии связи, рабочие точки, вычислительные машины, продавцы и др. По числу каналов СМО подразделяют на одноканальные и многоканальные. Заявки поступают в СМО обычно не регулярно, а случайно, образуя так называемый случайный поток заявок (требований). Обслуживание заявок также продолжается какое-то случайное время. Случайный характер потока заявок и времени обслуживания приводит к тому, что СМО оказывается загруженной неравномерно: в какие-то периоды времени скапливается очень большое количество заявок (они либо становятся в очередь, либо покидают СМО не обслуженными), в другие же периоды СМО работает с недогрузкой или простаивает. Предметом теории массового обслуживания является построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, характер потока заявок и т.п.) с показателями эффективности СМО, описывающими ее способность справляться с потоком заявок. В качестве показателей эффективности СМО используются: – Абсолютная пропускная способность системы (А), т.е. среднее число заявок, обслуживаемых в единицу времени; – относительная пропускная способность (Q), т.е. средняя доля поступивших заявок, обслуживаемых системой; – вероятность
отказа обслуживания заявки ( – среднее число занятых каналов (k); – среднее
число заявок в СМО ( – среднее
время пребывания заявки в системе ( – среднее
число заявок в очереди ( – среднее
время пребывания заявки в очереди ( – среднее число заявок, обслуживаемых в единицу времени; – среднее время ожидания обслуживания; – вероятность того, что число заявок в очереди превысит определенное значение и т.п. СМО делят на 2 основных типа: СМО с отказами и СМО с ожиданием (очередью). В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует (например, заявка на телефонный разговор в момент, когда все каналы заняты, получает отказ и покидает СМО не обслуженной). В СМО с ожиданием заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь на обслуживание. Одним из методов расчета показателей эффективности СМО является метод имитационного моделирования. Практическое использование компьютерного имитационного моделирования предполагает построение соответствующей математической модели, учитывающей факторы неопределенности, динамические характеристики и весь комплекс взаимосвязей между элементами изучаемой системы. Имитационное моделирование работы системы начинается с некоторого конкретного начального состояния. Вследствие реализации различных событий случайного характера, модель системы переходит в последующие моменты времени в другие свои возможные состояния. Этот эволюционный процесс продолжается до конечного момента планового периода, т.е. до конечного момента моделирования. 1. Основные характеристики CМО и показатели их эффективности 1.1 Понятие марковского случайного процессаПусть имеется некоторая система, которая с течением времени изменяет свое состояние случайным образом. В этом случае говорят, что в системе протекает случайный процесс. Процесс
называется процессом с дискретными состояниями, если его состояния Процесс работы СМО – это случайный процесс с дискретными состояниями и непрерывным временем. Случайный
процесс называют марковским или случайным процессом без последействия, если для
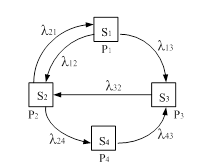
любого момента времени При анализе процессов работы СМО удобно пользоваться геометрической схемой – графом состояний. Обычно состояния системы изображаются прямоугольниками, а возможные переходы из состояния в состояние – стрелками. Пример графа состояний приведен на рис. 1.
Рис. 1. Поток событий последовательность однородных событий, следующих одно за другим в случайные моменты времени. Поток характеризуется интенсивностью λ – частотой появления событий или средним числом событий, поступающих в СМО в единицу времени. Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени. Поток событий
называется стационарным, если его вероятностные характеристики не зависят от
времени. В частности, интенсивность стационарного потока есть величина
постоянная: Поток событий
называется ординарным, если вероятность попадания на малый участок времени Поток событий
называется потоком без последействия, если для любых двух непересекающихся
участков времени Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия. 1.2 Уравнения КолмогороваВсе переходы
в системе из состояния в состояние происходят под некоторым потоком событий.
Пусть система Правило составлений уравнений Колмогорова: В левой части каждого из уравнений стоит производная по времени от вероятности данного состояния. В правой части стоит сумма произведений всех состояний, из которых возможен переход в данное состояние, на интенсивности соответствующих потоков событий минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного состояния. Например, для графа состояний, приведенного на рис. 1, уравнения Колмогорова имеют вид:
Т.к. в правой
части системы каждое слагаемое входит 1 раз со знаком
Следовательно, одно из уравнений системы можно отбросить и заменить уравнением (1.2.1). Чтобы получить конкретное решение надо знать начальные условия, т.е. значения вероятностей в начальный момент времени.
1.3 Финальные вероятности и граф состояний СМОПри
достаточно большом времени протекания процессов в системе (при
Смысл финальных вероятностей состоит в том, что они равны среднему относительному времени нахождения системы в данном состоянии. Т.к. в стационарном состоянии производные по времени равны нулю, то уравнения для финальных вероятностей получаются из уравнений Колмогорова путем приравнивания нулю их правых частей. Графы состояний, используемые в моделях систем массового обслуживания, называются схемой гибели и размножения. Такое название обусловлено тем, что эта схема используется в биологических задачах, связанных с изучением численности популяции. Его особенность состоит в том, что все состояния системы можно представить в виде цепочки, в которой каждое из состояний связано с предыдущим и последующим (рис 2).
Рис. 2. Граф состояний в моделях СМО Предположим, что все потоки, переводящие систему из одного состояния в другое, простейшие. По графу, представленному на рис. 2, составим уравнения для финальных вероятностей системы. Они имеют вид:
Получается
система из (n+1) уравнения, которая решается методом исключения.
Этот метод заключается в том, что последовательно все вероятности системы выражаются
через вероятность
Подставляя
эти выражения в последнее уравнение системы, находим 1.4 Показатели эффективности СМОЦель моделирования СМО состоит в том, чтобы рассчитать показатели эффективности системы через ее характеристики. В качестве показателей эффективности СМО используются: – абсолютная пропускная способность системы (А), т.е. среднее число заявок, обслуживаемых в единицу времени; – относительная пропускная способность (Q), т.е. средняя доля поступивших заявок, обслуживаемых системой; – вероятность
отказа ( – среднее число занятых каналов (k); – среднее
число заявок в СМО ( – среднее
время пребывания заявки в системе ( – среднее
число заявок в очереди ( – среднее
число заявок в системе ( – среднее
время пребывания заявки в очереди ( – среднее
время пребывания заявки в системе ( – степень
загрузки канала ( – среднее число заявок, обслуживаемых в единицу времени; – среднее время ожидания обслуживания; – вероятность того, что число заявок в очереди превысит определенное значение и т.п. Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания, среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (очереди), деленному на интенсивность потока заявок, т.е.
Формулы (1.4.1)
и (1.4.2) называются формулами Литтла. Они вытекают из того, что в предельном
стационарном режиме среднее число заявок, прибывающих в систему, равно среднему
числу заявок, покидающих ее, т.е. оба потока заявок имеют одну и ту же
интенсивность Формулы для вычисления показателей эффективности приведены в таб. 1. Таблица 1.
1.5 Основные понятия имитационного моделированияОсновная цель имитационного моделирования заключается в воспроизведении поведения изучаемой системы на основе анализа наиболее существенных взаимосвязей ее элементов. Компьютерное имитационное моделирование следует рассматривать как статический эксперимент. Из теории
функций случайных величин известно, что для моделирования случайной величины
Предположим,
что в некоторой системе массового обслуживания время обслуживания одной заявки
распределено по экспоненциальному закону с параметром
Пусть |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
При
достаточно большом времени протекания процессов в системе (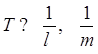 ) могут устанавливаться
вероятности состояний, не зависящие от времени, которые называются финальными
вероятностями, т.е. в системе устанавливается стационарный режим. Если число
состояний системы конечно, и из каждого из них за конечное число шагов можно
перейти в любое другое состояние, то финальные вероятности существуют, т.е.
) могут устанавливаться
вероятности состояний, не зависящие от времени, которые называются финальными
вероятностями, т.е. в системе устанавливается стационарный режим. Если число
состояний системы конечно, и из каждого из них за конечное число шагов можно
перейти в любое другое состояние, то финальные вероятности существуют, т.е. ![]()
Т.к. в стационарном состоянии производные по времени равны 0, то уравнения для финальных вероятностей получаются из уравнений Колмогорова путем приравнивания правых частей 0. Запишем уравнения для финальных вероятностей для нашей СМО.
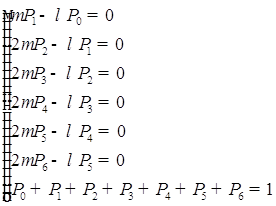
Решим данную систему линейных уравнений с помощью программного пакета Maple 11 (см. Приложение 1).
Получим финальные вероятности системы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Сравнение
вероятностей, полученных из системы уравнений Колмогорова при ![]() , с финальными
вероятностями показывает, что ошибки
, с финальными
вероятностями показывает, что ошибки ![]() равны:
равны:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Т.е. достаточно малы. Это подтверждает правильность полученных результатов.
2.3 Расчет показатели эффективности системы по финальным вероятностям
Найдем показатели эффективности системы массового обслуживания.
Сначала вычислим приведенную интенсивность потока заявок:
![]()
1) Вероятность отказа в обслуживании заявки, т.е. вероятность того, что заявка покидает систему не обслуженной. В нашем случае заявке отказывается в обслуживании, если все 2 канала заняты, и очередь максимально заполнена (т.е. 4 человек в очереди), это соответствует состоянию системы S6. Т.к. вероятность прихода системы в состояние S6 равна Р6, то
![]()
2) Относительная пропускная способность – это средняя доля поступивших заявок, обслуживаемых системой.
![]()
3) Абсолютная пропускная способность – это среднее число заявок, обслуживаемых в единицу времени.
![]()
4) Средняя длина очереди, т.е.
среднее число заявок в очереди, равна сумме произведений числа заявок в очереди
на вероятность соответствующего состояния. ![]()
5) Среднее время пребывания заявки в очереди определяется формулой Литтла:
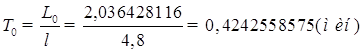
6) Среднее число занятых каналов определяется следующим образом:
3. Имитационное моделирование СМО
3.1 Алгоритм метода имитационного моделирования СМО (пошаговый подход)
Рассмотрим двухканальную систему массового обслуживания (n = 2) с максимальной длиной очереди равной шести (m = 4). В СМО поступает простейший поток заявок со средней интенсивностью λ = 4,8 и показательным законом распределения времени между поступлением заявок. Поток обслуживаемых в системе заявок является простейшим со средней интенсивностью μ = 2 и показательным законом распределения временем обслуживания.
Для имитации СМО воспользуемся одним из методов статистического моделирования – имитационным моделированием. Будем использовать пошаговый подход. Суть этого подхода в том, что состояния системы рассматриваются в последующие моменты времени, шаг между которыми является достаточно малым, чтобы за его время произошло не более одного события.
Выберем шаг
по времени (![]() ). Он должен быть много
меньше среднего времени поступления заявки (
). Он должен быть много
меньше среднего времени поступления заявки (![]() )
и среднего времени ее обслуживания (
)
и среднего времени ее обслуживания (![]() ), т.е.
), т.е.
![]() , где (3.1.1)
, где (3.1.1)
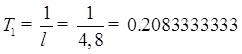
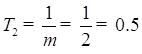
Исходя из
условия (3.1.1) определим шаг по времени ![]() .
.
Время поступления заявки в СМО и время ее обслуживания являются случайными величинами. Поэтому, при имитационном моделировании СМО их вычисление производится с помощью случайных чисел.
Рассмотрим поступление
заявки в СМО. Вероятность того, что на интервале ![]() в
СМО поступит заявка, равна:
в
СМО поступит заявка, равна: 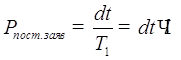 .
Сгенерируем случайное число
.
Сгенерируем случайное число ![]() , и,
если
, и,
если ![]() , то будем считать, что
заявка на данном шаге в систему поступила, если
, то будем считать, что
заявка на данном шаге в систему поступила, если ![]() ,
то не поступила.
,
то не поступила.
В программе
это осуществляет isRequested(). Интервал времени ![]() примем
постоянным и равным 0,0001, тогда отношение
примем
постоянным и равным 0,0001, тогда отношение ![]() будет
равно 10000. Если заявка поступила, то она принимает значение «истина», в
противном случае значение «ложь».
будет
равно 10000. Если заявка поступила, то она принимает значение «истина», в
противном случае значение «ложь».
bool isRequested()
{
double r = R. NextDouble();
if (r < (timeStep * lambda))
{return true;}
return false;
}
Рассмотрим
теперь обслуживание заявки в СМО. Время обслуживания заявки в системе
определяется выражением 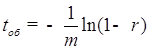 , где
, где ![]() – случайное число. В
программе время обслуживания определяется с помощью функции GetServiceTime().
– случайное число. В
программе время обслуживания определяется с помощью функции GetServiceTime().
double GetServiceTime()
{
double r = R. NextDouble();
return (-1/mu*Math. Log (1-r, Math.E));
}
Алгоритм метода имитационного моделирования можно сформулировать следующим образом. Время работы СМО (Т) разбивается на шаги по времени dt, на каждом из них выполняется ряд действий. Вначале определяются состояния системы (занятость каналов, длина очереди), затем, с помощью функции isRequested(), определяется, поступила ли на данном шаге заявка или нет.
Если поступила, и, при этом имеются свободные каналы, то с помощью функции GetServiceTime() генерируем время обработки заявки и ставим ее на обслуживание. Если все каналы заняты, а длина очереди меньше 4, то помещаем заявку в очередь, если же длина очереди равна 4, то заявке будет отказано в обслуживании.
В случае, когда на данном шаге заявка не поступала, а канал обслуживания освободился, проверяем, есть ли очередь. Если есть, то из очереди заявку ставим на обслуживание в свободный канал. После проделанных операций время обслуживания для занятых каналов уменьшаем на величину шага dt.
По истечении времени Т, т.е., после моделирования работы СМО, вычисляются показатели эффективности работы системы и результаты выводятся на экран.
3.2 Блок-схема программы
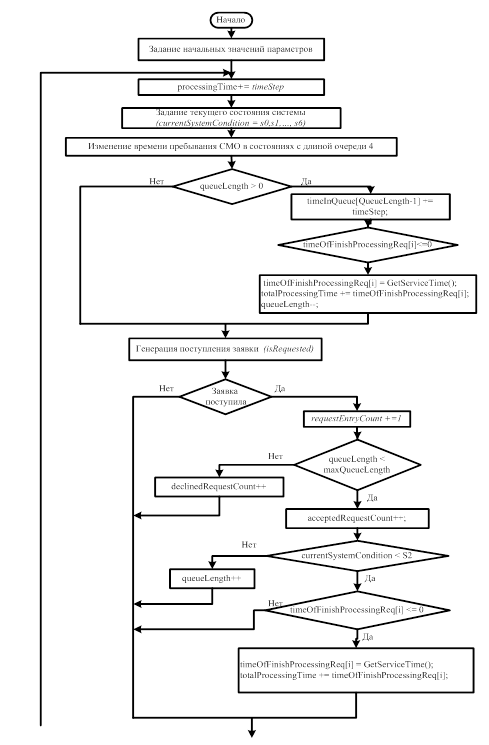
Блок-схема программы, реализующей описанный алгоритм, приведена на рис. 5.
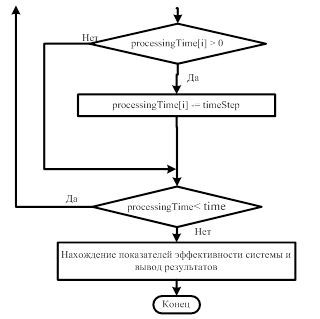
Рис. 5. Блок-схема программы
Распишем некоторые блоки более подробно.
Блок 1. Задание начальных значений параметров.
Random R; // Генератор случайных чисел
public uint maxQueueLength; // Максимальная длина очереди
public uint channelCount; // Число каналов в системе
public double lambda; // Интенсивность потока поступления заявок
public double mu; // Интенсивность потока обслуживания заявок
public double timeStep; // Шаг по времени
public double[] timeOfFinishProcessingReq; // Время окончания обслуживания заявки во всех каналах
public double[] timeInQueue; // Время пребывания СМО в состояниях с очередью
public double processingTime; // Время работы системы
public double totalProcessingTime; // Суммарное время обслуживания заявок
public uint requestEntryCount; // Число поступивших заявок
public uint declinedRequestCount; // Число отказанных заявок
public uint acceptedRequestCount; // Число обслуженных заявок
uint queueLength; // Длина очереди //
Тип, описывающий состояния СМО
enum SysCondition {S0, S1, S2, S3, S4, S5, S6};
SysCondition currentSystemCondition; // Текущее состояние системы
Задание состояний системы. Выделим у данной 2-х канальной системы 7 различных состояний: S0, S1. S6. СМО находится в состоянии S0, когда система свободна; S1 – хотя бы один канал свободен; в состоянии S2, когда все каналы заняты, и есть место в очереди; в состоянии S6 – все каналы заняты, и очередь достигла максимальной длины (queueLength = 4).
Определяем текущее состояние системы с помощью функции GetCondition()
SysCondition GetCondition()
{
SysCondition p_currentCondit = SysCondition.S0;
int k = 0;
int busyChannelCount = 0;
for (int i = 0; i < channelCount; i++)
{
if (timeOfFinishProcessingReq[i] > 0)
{
k = 1;
busyChannelCount++;
}
else
{k = 0;}
p_currentCondit += k * (i + 1);
}
if (busyChannelCount > 1)
{p_currentCondit ++;}
return p_currentCondit + (int) QueueLength;
}
Изменение времени пребывания СМО в состояниях с длиной очереди 1, 2,3,4. Это реализуется следующим программным кодом:
if (queueLength > 0)
{
timeInQueue [queueLength – 1] += timeStep;
if (queueLength > 1)
{timeInQueue [queueLength – 2] += timeStep;}
}
Присутствует такая операция, как помещение заявки на обслуживание в свободный канал. Просматриваются, начиная с первого, все каналы, когда выполняется условие timeOfFinishProcessingReq [i] <= 0 (канал свободен), в него подается заявка, т.е. генерируется время окончания обслуживания заявки.
for (int i = 0; i < channelCount; i++)
{
if (timeOfFinishProcessingReq [i] <= 0)
{
timeOfFinishProcessingReq [i] = GetServiceTime();
totalProcessingTime+= timeOfFinishProcessingReq [i];
break;
}
}
Обслуживание заявок в каналах моделируется кодом:
for (int i = 0; i < channelCount; i++)
{
if (timeOfFinishProcessingReq [i] > 0)
{
timeOfFinishProcessingReq [i] -= timeStep;
}
}
Алгоритм метода имитационного моделирования реализован на языке программирования C#.
3.3 Расчет показателей эффективности СМО на основе результатов ее имитационного моделирования
Наиболее важными являются такие показатели, как:
1) Вероятность отказа в обслуживании заявки, т.е. вероятность того, что заявка покидает систему не обслуженной. В нашем случае заявке отказывается в обслуживании, если все 2 канала заняты, и очередь максимально заполнена (т.е. 4 человек в очереди). Для нахождения вероятности отказа разделим время пребывания СМО в состоянии с очередью 4 на общее время работы системы.
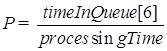
2) Относительная пропускная способность – это средняя доля поступивших заявок, обслуживаемых системой.
![]()
3) Абсолютная пропускная способность – это среднее число заявок, обслуживаемых в единицу времени.
![]()
4) Длина очереди, т.е. среднее число заявок в очереди. Длина очереди равна сумме произведений числа человек в очереди на вероятность соответствующего состояния. Вероятности состояний найдем как отношение времени нахождения СМО в этом состоянии к общему времени работы системы.
![]()
5) Среднее время пребывания заявки в очереди определяется формулой Литтла
![]()
6) Среднее число занятых каналов определяется следующим образом:
![]()
7) Процент заявок, которым было отказано в обслуживании, находится по формуле
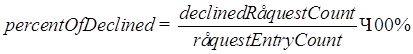
8) Процент обслуженных заявок находится по формуле
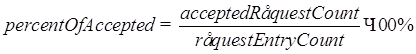
3.4 Статистическая обработка результатов и их сравнение с результатами аналитического моделирования
Т.к. показатели эффективности получаются в результате моделирования СМО в течение конечного времени, они содержат случайную компоненту. Поэтому, для получения более надежных результатов нужно провести их статистическую обработку. С этой целью оценим доверительный интервал для них по результатам 20 прогонов программы.
Величина ![]() попадает в доверительный
интервал, если выполняется неравенство
попадает в доверительный
интервал, если выполняется неравенство
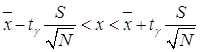 , где
, где
![]() математическое ожидание
(среднее значение), находится по формуле
математическое ожидание
(среднее значение), находится по формуле
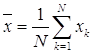 ,
,
![]() исправленная дисперсия,
исправленная дисперсия,
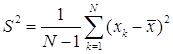 ,
,
N=20 – число прогонов,
![]() – надежность. При
– надежность. При ![]() и N=20
и N=20 ![]() .
.
Результат работы программы представлен на рис. 6.
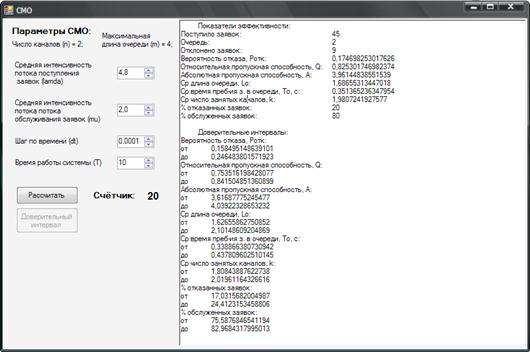
Рис. 6. Вид программы
Для удобства сравнения результатов, полученных различными методами моделирования, представим их в виде таблицы.
Таблица 2.
|
Показатели эффективности СМО |
Результаты аналитического моделирования |
Результаты имитационного моделирования (послед. шаг) |
Результаты имитационного моделирования |
|
|
Нижняя граница доверительного интервала |
Верхняя граница доверительного интервала |
|||
| Вероятность отказа |
|
0,174698253017626 | 0,158495148639101 | 0,246483801571923 |
| Относительная пропускная способность |
|
0,825301746982374 | 0,753516198428077 | 0,841504851360899 |
| Абсолютная пропускная способность |
|
3,96144838551539 | 3,61687775245477 | 4,03922328653232 |
| Средняя длина очереди |
|
1,68655313447018 | 1,62655862750852 | 2,10148609204869 |
| Среднее время пребывания заявки в очереди | 0,4242558575 | 0,351365236347954 | 0,338866380730942 | 0,437809602510145 |
| Среднее число занятых каналов |
|
1,9807241927577 | 1,80843887622738 | 2,01961164326616 |
Из табл. 2 видно, что результаты, полученные при аналитическом моделировании СМО, попадают в доверительный интервал, полученный по результатам имитационного моделирования. Т.е., результаты, полученные разными методами, согласуются.
Заключение
В данной работе рассмотрены основные методы моделирования СМО и расчета показателей их эффективности.
Проведено моделирование двухканальной СМО с максимальной длиной очереди равной 4 с помощью уравнений Колмогорова, а также, найдены финальные вероятности состояний системы. Рассчитаны показатели ее эффективности.
Проведено имитационное моделирование работы такой СМО. На языке программирования C# составлена программа, имитирующая ее работу. Проведена серия расчетов, по результатам которых найдены значения показателей эффективности системы и выполнена их статистическая обработка.
Полученные при имитационном моделировании результаты согласуются с результатами аналитического моделирования.
Литература
1. Вентцель Е.С. Исследование операций. – М.: Дрофа, 2004. – 208 с.
2. Волков И.К., Загоруйко Е.А. Исследование операций. – М.: Изд.-во МГТУ им. Н.Э. Баумана, 2002. – 435 с.
3. Волков И.К., Зуев С.М., Цветкова Г.М. Случайные процессы. – М.: Изд.-во МГТУ им. Н.Э. Баумана, 2000. – 447 с.
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979. – 400 с.
5. Ивницкий В.Л. Теория сетей массового обслуживания. – М.: Физматлит, 2004. – 772 с.
6. Исследование операций в экономике/ под ред. Н.Ш. Кремера. – М.: Юнити, 2004. – 407 с.
7. Таха Х.А. Введение в исследование операций. – М.: ИД «Вильямс», 2005. – 902 с.
8. Харин Ю.С., Малюгин В.И., Кирлица В.П. и др. Основы имитационного и статистического моделирования. Минск: Дизайн ПРО, 1997. – 288 с.
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


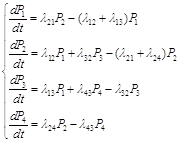
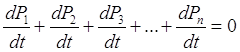 ,
,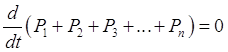 ,
,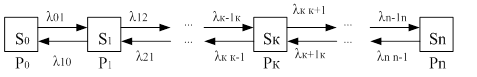
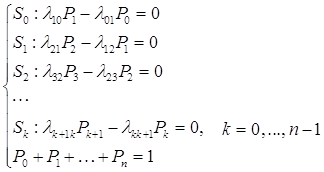
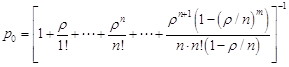
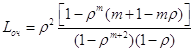
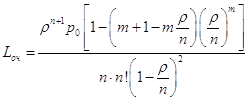
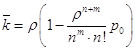
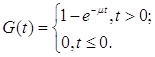
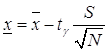 ,
, 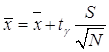 , т.е.
, т.е. 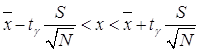 , где
, где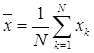 ,
,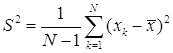 ,
,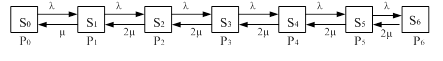
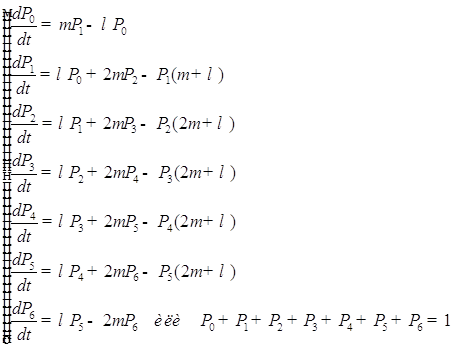
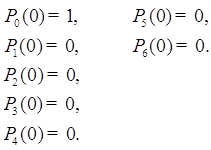
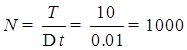 . Последовательно N раз вычисляя
. Последовательно N раз вычисляя