|
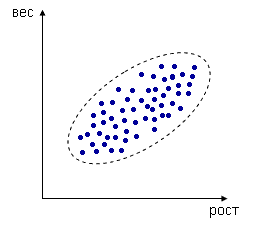
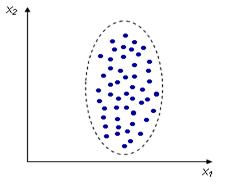
Курсовая работа: Расчет коэффициента корреляции между притоком прямых иностранных инвестиций и темпами экономического роста на примере Великобритании и ВенгрииКурсовая работа: Расчет коэффициента корреляции между притоком прямых иностранных инвестиций и темпами экономического роста на примере Великобритании и ВенгрииКУРСОВАЯ РАБОТА «Расчет коэффициента корреляции между притоком прямых иностранных инвестиций и темпами экономического роста на примере Великобритании и Венгрии Содержание Введение 1. Теоретические аспекты изучения корреляционных связей в экономике 1.1 Корреляционный анализ 1.2 Краткая экономическая характеристика Великобритании 1.3 Краткая экономическая характеристика Венгрии 2. Корреляционный анализ экономики 2.1 Анализ основных показателей прироста иностранных инвестиций 2.2 Анализ корреляционных связей и темпов экономического роста Заключение Список литературы Введение Актуальность темы данной работы определяется тем, что обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности. Вообще говоря, трудно назвать ту сферу, в которой она бы не использовалась. Но, пожалуй, ни в одной области знаний и практической деятельности обработка статистических данных не играет такой исключительно большой роли, как в экономике, имеющей дело с обработкой и анализом огромных массивов информации о социально-экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимает корреляционный и регрессионный анализы обработки статистических данных. В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и регрессионного анализа. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и не только выявить, но и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под причинной зависимостью понимается такая связь между процессами, когда изменение одного из них является следствием изменения другого. Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом. Использование возможностей современной вычислительной техники, оснащенной пакетами программ машинной обработки статистической информации на ЭВМ, делает практически осуществимым оперативное решение задач изучения взаимосвязи показателей биржевых ставок методами корреляционно-регрессионного анализа. Цель работы определить коэффициент корреляции между притоками ПИИ и темпами экономического роста развитой и развивающейся страны В связи с поставленной целью необходимо решить ряд задач: – дать понятие корреляционному анализу – дать характеристику экономики Великобритании – дать характеристику экономики Венгрии – Провести анализ между прямыми иностранными инвестициями и ростом ВВП страны 1. Теоретические аспекты изучения корреляционных связей в экономике 1.1 Корреляционный анализ Корреляционный анализ – метод, позволяющий обнаружить зависимость между несколькими случайными величинами. Допустим, проводится независимое измерение различных параметров у одного типа объектов. Из этих данных можно получить качественно новую информацию – о взаимосвязи этих параметров. Например, измеряем рос и вес человека, каждое измерение представлено точкой в двумерном пространстве:
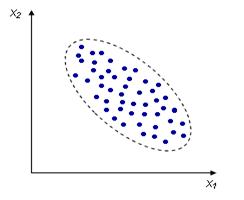
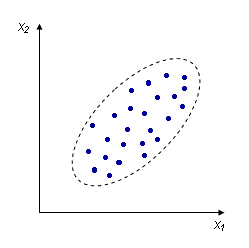
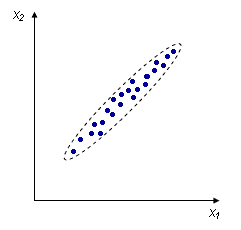
Несмотря на то, что величины носят случайный характер, в общем наблюдается некоторая зависимость – корреляция. В данном случае это положительная корреляция (при увеличении одного параметра второй тоже увеличивается). Возможны также такие случаи:
Корреляцию необходимо охарактеризовать численно, чтобы, например, различать такие случаи:
Для этого вводится коэффициент корреляции. Он рассчитывается следующим образом: Есть массив из n точек {x1, i, x2, i} Рассчитываются средние значения для каждого параметра:
И коэффициент корреляции:
r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x1 и x2: r равен 1 (или -1), если связь линейна. Коэффициент корреляции является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы: 1. Коэффициент корреляции значимо отличается от нуля (т.е. корреляция есть): Тестовая статистика вычисляется по формуле:
и
сравнивается с табличным значением коэффициента Стьюдента t (p = 0.95, f = Если тестовая статистика больше табличного значения, то коэффициент значимо отличается от нуля. По формуле видно, что чем больше измерений n, тем лучше (больше тестовая статистика, вероятнее, что коэффициент значимо отличается от нуля) 2. Отличие между двумя коэффициентами корреляции значимо: Тестовая статистика:
Также
сравнивается с табличным значением t (p, Методами корреляционного анализа решаются следующие задачи: 1) Взаимосвязь. Есть ли взаимосвязь между параметрами? 2) Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым. 3) Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации. 1.2 Краткая экономическая характеристика Великобритании Великобритания высокоразвитая индустриальная страна, входит в первую пятерку наиболее развитых государств мира. По запасам энергоресурсов Великобритания занимает 1-е место в Европе и является крупным производителем нефти и газа Главной особенностью макроэкономического развития страны является то, что Великобритания выбрала неолиберальную, «англосаксонскую» модель развития. Для нее характерно преобладание свободного частного предпринимательства (более 80% общего объема производства). Частный сектор обеспечивает свыше 75% всех рабочих мест. Политика британского правительства направлена на создание максимально благоприятных возможностей для развития частного бизнеса. Однако при общем повышении жизненного уровня населения в стране наблюдается значительная поляризация доходов, когда 10% населения владеют 54% национального богатства. Великобритания в международном разделении труда выступает как поставщик промышленной продукции. Вместе с тем экономическая роль Великобритании в современном мире определяется не только промышленной, но и банковской, страховой, судо-фрахтовой и другой коммерческой деятельностью. Около 30% ее валового национального продукта поступает от обрабатывающей промышленности и 45% – от сферы обслуживания, включающей транспорт и связь, розничную торговлю, страхование, банки и другие финансовые учреждения, здравоохранение и образование. Доля сферы обслуживания в валовом национальном продукте увеличивается значительно быстрее, чем доля обрабатывающей промышленности, которая даже несколько снижается. Уменьшилась также доля сельского хозяйства – до 3% и добывающей промышленности до 1,4%. Вывоз промышленных товаров и экспорт «услуг» для развития экономики Великобритании имеет исключительное значение, которые вместе дают 26% валового национального продукта. Важной статьей дохода британских международных монополий был и остается вывоз капитала в другие страны. С переориентацией британской промышленности на новейшие отрасли для ее развития внешний рынок стал играть большую роль, чем дешевая рабочая сила. В последнее время этот рынок британские монополии находят в развитых капиталистических странах, доля которых в вывозе британского капитала превысила 3/5. Все еще велик экспорт капитала Великобритании в развивающиеся страны: на нее приходится почти половина капитала вывозимого в эти страны западноевропейскими государствами. В то же время быстро растут вклады иностранных монополий в экономику Великобритании. Великобритания, потеряв почти все свои колонии, утратила многие экономические преимущества: контроль над богатейшими мировыми месторождениями – цветных металлов, нефти, важными источниками натурального каучука, дешевой сельскохозяйственной продукции, гарантированные рынки сбыта промышленных товаров и безграничные возможности вывоза капитала на все континенты. Будучи должником США и их «младшим» партнером и взяв на себя значительные расходы по НАТО, Великобритания вынуждена мириться с проникновением в ее экономику американского капитала, роль которого возрастает с каждым годом. Деньги магнатов из-за океана вкладываются преимущественно в быстро развивающиеся современные отрасли промышленности. Американскими фирмами выпускается свыше половины автомобилей, 3/5 ЭВМ и такая же доля медикаментов. Более половины компаний, занятых разведкой месторождений нефти и газа в Северном море – также американские. 1.3 Краткая экономическая характеристика Венгрии Венгрия новая постсоциалистическая страна Центральной Европы с экономикой, в которой уже утвердились основные рыночные принципы. Современный уровень экономического и социального развития Венгрии эксперты считают одним из самых высоких среди стран Центральной и Юго-Восточной Европы. Венгерская экономика в значительной мере ориентирована на Европейский Союз. Благоприятная в начале 2000 г. конъюнктура в странах ЕС способствовала ускоренному экономическому росту и в Венгрии: в I квартале ВВП возрос на 6,6% по сравнению с аналогичным периодом 1999 г. Наметившееся к концу 2000 г. замедление темпов экономического роста в Евросоюзе сыграло определяющую роль в снижении темпов роста и в Венгрии. Тем не менее, в целом за 2000 г. Венгрии удалось сохранить за собой одно из лидирующих мест среди стран региона по темпам экономического роста (5,3% при среднем темпе прироста по странам Центральной Европы порядка 4,2%). Форсированный приток иностранного капитала привел к коренной перестройке структуры венгерской экономики. В Венгрии за последние годы сформировалась индустриально-аграрная структура экономики западноевропейского типа: промышленность и строительство обеспечивают более 30% произведенного ВВП, сельское хозяйство – около 5%, а сфера услуг – 65%. Довольно прочным и устойчивым представляется нынешнее валютно-финансовое положение Венгрии. Несмотря на значительное ухудшение для страны условий внешней торговли, в допустимых пределах удается удерживать дефицит внешнеторгового и платежного балансов страны. Степень либерализации внешнеторгового режима, осуществленной в Венгрии, оценивается секретариатом ВТО в основном положительно, хотя отмечается сравнительно высокий средний уровень таможенных пошлин, применяемых Венгрией в рамках режима наибольшего благоприятствования. Розничный товарооборот на внутреннем рынке после спада 1987–1997 гг. постоянно расширяется (в 2002 г. – 24,8 млн. долл.). Этому способствуют рост денежных доходов населения, появление новых видов торговли (гипермаркетов, торговых центров) и повышение качества обслуживания. Структура товарооборота приблизительно таклва: 33,4% – продовольствие, 28,4% – транспортные средства, запчасти и топливо к ним, 16,4% – мебель и бытовая техника, 9,5% – товары культурно-познавательного назначения. В Будапеште 25 ноября 2005 г. состоялась конференция «Динамичная экономика», в ходе которой министр финансов Венгрии Я. Вереш, подводя итоги развития венгерской экономики за последние годы, отметил, что рост венгерского ВВП как по номиналу, так и по паритету покупательной способности был наивысшим среди стран региона. Устойчивый рост экспорта свидетельствует о том, что выпускаемая Венгрией продукция качественна и пользуется спросом на мировых рынках. Источниками роста венгерской экономики являются, в первую очередь, инвестиции транснациональных корпораций и государственные капиталовложения. Эра транснациональных корпораций и производства продуктов с низкой долей добавленной стоимости подошла к концу, поэтому экономическая стратегия должна меняться 2. Корреляционный анализ экономики 2.1 Анализ основных показателей прироста иностранных инвестиций Таблица 1 Исходные данные
Таблица 2 Темпы прироста показателей для Венгрия
Таблица 3 Темпы прироста показателей для Великобритании
Коэффициент роста цепным методом рассчитывается по формуле: Кpц = Средний коэффициент роста цепным методом рассчитывается по формуле:
Как следует из сравнительного анализа динамики данных социально-экономических показателей развития, Великобритания превосходит венгрия по всем показателям роста, кроме темпов роста численности населения. При этом особенно заметно преимущество Великобритании по сравнению с Венгрия в темпах роста привлечения в страну иностранных инвестиций, как flow, так и stock. Поскольку Великобритания более заметно превосходит Венгрия в темпах роста ВВП, чем Венгрия превосходит Великобритания в темпах роста населения, то как следствие Великобритания имеет более высокие темпы роста среднедушевого ВВП. Таблица 4 Расчетные корреляции ВВП и инвестиций flow для Венгрия
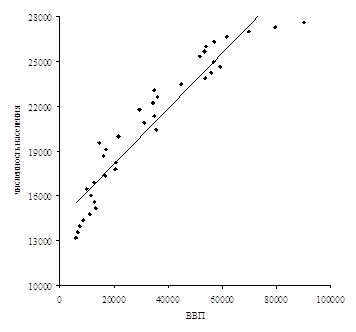
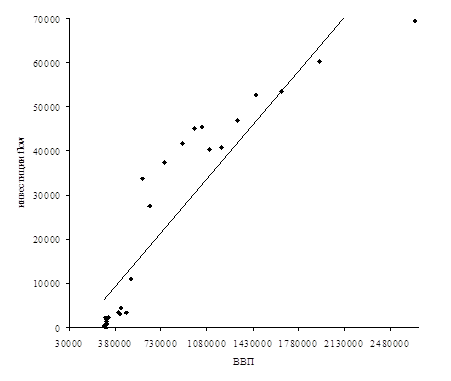
Приведем расчет корреляционной зависимости на примере ВВП и инвестиций flow для Венгрия. Проведем визуальный анализ данных путем построения корреляционного поля зависимости инвестиций flow от ВВП.
Рисунок 1 Корреляционное поле зависимости инвестиций flow от ВВП Проанализировав данные и их графическое изображение, можно сделать предположение, что связь между признаками линейная и она описывается уравнением прямой: х2 = а0 + а1 ∙ х1. (3) Определим параметры уравнения прямой на основе метода наименьших квадратов, решив систем нормальных уравнений.
Откуда:
По формулам (5), (6) вычислим а0, а1, используя расчетные данные таблицы 4.
Вычислив параметры, получим следующее уравнение регрессии: х2 = -602,190 + 0,042 ∙ х1. Следовательно, с увеличением ВВП на 1 млн. долл., инвестиции flow увеличатся на 0,42% млн. долл. Значимость коэффициентов регрессии проверим по t-критерию Стьюдента. Вычислим расчетные значения t-критерия по формулам: для параметра а0:
для параметра а1:
где n – объем выборки, среднее квадратическое отклонение результативного признака у от выровненных значений ух:
среднее квадратическое отклонение факторного признака х от общей
средней
Находим:
Вычисленные значения ta0 и ta1 сравнивают с критическими (табличными) t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v = n -2 = 37–2 =35. В социально-экономических исследованиях уровень значимости а обычно принимают равным 0,05. Параметр признается значимым при условии, если tрасч> tтабл. Так как tрасча0 = 5,611 больше tтабл = 3,000, параметр а0 признается значимым, т.е. в этом случае мало вероятно, что найденное значение параметра обусловлено только случайными совпадениями. Так как tрасча1 = 8,686 больше tтабл = 3,000, следовательно, параметр а1 также признается значимым. Выявим тесноту корреляционной связи между х и у с помощью линейного коэффициента корреляции, используя формулу:
Т.к. линейный коэффициент корреляции r = 0,827, то связь между инвестициями flow и ВВП прямая, очень высокая связь. Значимость линейного коэффициента корреляции определяется помощью t-критерия Стьюдента (число степеней свободы = 35, уровень значимости а = 0,05) по формуле:
Так как Определим линейный коэффициент детерминации r2: r2 = 0,8272 = 0,683. Он показывает, что 68,3% вариации инвестиций flow обусловлено вариацией ВВП. Теоретическое корреляционное отношение η определим по формуле:
Т.к. r = η, то будем считать, что линейная форма связи между х1 и х2, выбрана верно. Аналогично проведем расчет корреляции для остальных параметров. Уравнение регрессии: х3 = 2211,412 + 3,316 ∙ х2.
Вычисленные значения ta0 и ta1 сравнивают с критическими (табличными) t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v = n -2 = 27–2 = 25 при уровне значимости а = 0,05. Таблица 5 Расчетные корреляции инвестиций flow и stock для Венгрия
Так как tа0 = 3,007 меньше tтабл = 3,080, параметр а0 признается незначимым. Так как tа1 = 5,437 больше tтабл = 3,080, следовательно, параметр а1 признается значимым. Линейный коэффициент корреляции:
Т.к. r = 0,723, то связь между инвестициями stock и flow, прямая, высокая связь. Так как Определим линейный коэффициент детерминации r2: r2 = 0,7232 = 0,523. Он показывает, что 52,3% вариации инвестиций stock обусловлено вариацией инвестиций flow. Т.к. r = η, то будем считать, что линейная форма связи между х2 и х3, выбрана верно. 2.2 Анализ корреляционных связей и темпов экономического роста Таблица 6 Расчетные корреляции ВВП и численности населения для Венгрия
Рисунок 3 Корреляционное поле зависимости численности населения от ВВП Вычислив параметры, получим следующее уравнение регрессии: х4 = 14400,251 + 0,186 ∙ х1.
Вычисленные значения ta0 и ta1 сравнивают с критическими (табличными) t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v = n -2 = 37–2 = 35 при уровне значимости а = 0,05. Так как tа0 = 59,725 меньше tтабл = 3,000, параметр а0 признается значимым. Так как tа1 = 17,349 больше tтабл = 3,000, следовательно, параметр а1 признается значимым. Линейный коэффициент корреляции:
Т.к. r = 0,946, то связь между ВВП и численностью населения Венгрия прямая, полная связь. Так как Линейный коэффициент детерминации r2: r2 = 0,9462 = 0,896. Он показывает, что 89,6% вариации численности населения Венгрия обусловлено вариацией ВВП. Т.к. r = η, то будем считать, что линейная форма связи между х1 и х4, выбрана верно. Таблица 7 Расчетные корреляции ВВП и инвестиций flow для Великобритании
Рисунок 4 Корреляционное поле зависимости инвестиций flow от ВВП Уравнение регрессии: у2 = -3868,309 + 0,035 ∙ у1.
Так как tрасча0 = 2,143 меньше tтабл = 3,000, параметр а0 признается незначимым, т.е. в этом случае вероятно, что найденное значение параметра обусловлено только случайными совпадениями. Так как tрасча1 = 12,480 больше tтабл = 3,000, следовательно, параметр а1 также признается значимым. Линейный коэффициент корреляции:
Т.к. линейный коэффициент корреляции r = 0,928, то связь между инвестициями flow и ВВП прямая, полная связь. Так как Линейный коэффициент детерминации r2: r2 = 0,9282 = 0,862. Он показывает, что 86,2% вариации инвестиций flow обусловлено вариацией ВВП. Т.к. r = η, то будем считать, что линейная форма связи между у1 и у2, выбрана верно. Уравнение регрессии: у3 = -3159,825 + 3,939 ∙ у2.
Так как tа0 = 0,759 меньше tтабл = 3,080, параметр а0 признается незначимым. Таблица 8 Расчетные корреляции инвестиций flow и stock для Великобритании
Так как tа1 = 22,950 больше tтабл = 3,080, следовательно, параметр а1 признается значимым. Линейный коэффициент корреляции:
Т.к. r = 0,975, то связь между инвестициями stock и flow, прямая, полная. Так как Определим линейный коэффициент детерминации r2: r2 = 0,9752 = 0,951. Он показывает, что 95,1% вариации инвестиций stock обусловлено вариацией инвестиций flow. Т.к. r = η, то будем считать, что линейная форма связи между х2 и х3, выбрана верно.
Рисунок 6 Корреляционное поле зависимости численности населения от ВВП Вычислив параметры, получим следующее уравнение регрессии: у4 = 960230,354 + 0,189 ∙ у1.
Так как tа0 = 70,696 больше tтабл = 3,000, параметр а0 признается значимым. Так как tа1 = 8,825 больше tтабл = 3,000, следовательно, параметр а1 признается значимым. Линейный коэффициент корреляции:
Т.к. r = 0,831, то связь между ВВП и численностью населения Великобритании прямая, полная связь. Так как Линейный коэффициент детерминации r2: r2 = 0,8312 = 0,690. Он показывает, что 69,0% вариации численности населения Великобритании обусловлено вариацией ВВП. Т.к. r = η, то будем считать, что линейная форма связи между х1 и х4, выбрана верно. Заключение Таким образом, значимыми приняты все рассмотренные связи: 1) между инвестициями flow и ВВП Венгрия (прямая, очень высокая связь); 2) между инвестициями stock и flow (прямая, высокая связь); 3) между ВВП и численностью населения Венгрия (прямая, полная связь); 4) между инвестициями flow и ВВП Великобритании (прямая, полная связь); 5) между инвестициями stock и flow Великобритании (прямая, полная связь); 6) между ВВП и численностью населения Великобритании (прямая, полная связь). Незначимым признан параметр а0 для связей: 1) между инвестициями stock и flow Венгрия; 2) между инвестициями flow и ВВП Великобритании; 3) между инвестициями stock и flow Великобритании. В целом все исследованные модели являются адекватными и на их основе можно делать прогнозы. Список литературы 1. В.А. Колемаев, О.В. Староверов, В.Б. Турундаевский «Теория вероятностей и математическая сатистика»/ М., 1991. 2. «Теория Статистики» под редакцией Р.А. Шмойловой/ «ФиС», 1998. 3. «Многомерный статистический анализ на ЭBM с использованием пакета Microsoft Excel»/ М., 1997. 4. А.А. Френкель, Е.В. Адамова «Корреляционно регрессионный анализ в экономических приложениях»/ М., 1987. 5. И.Д. Одинцов «Теория статистики»/ М., 1998. 6. А.Н. Кленин, К.К. Шевченко «Математическая статистика для экономистов-статистиков»/ М., 1990. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


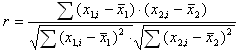
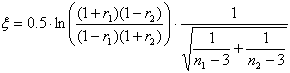

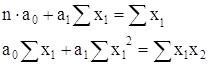 (4)
(4)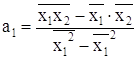 (5)
(5)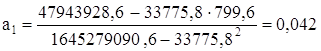 .
.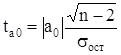 , (7)
, (7)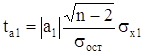 , (8)
, (8)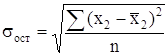 , (9)
, (9)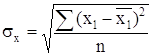 . (10)
. (10)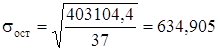 ,
,  ,
,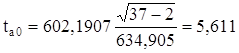 ,
, 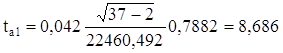 .
.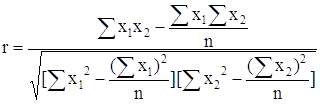 . (11)
. (11)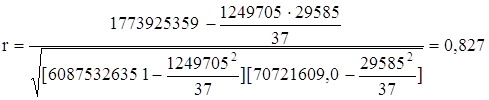 .
.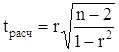 . (12)
. (12)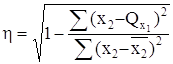 . (13)
. (13)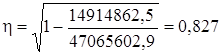 .
.