|
Контрольная работа: Отрицания и антитезы в E-структурахКонтрольная работа: Отрицания и антитезы в E-структурахОтрицания и антитезы в E-структурах Когда речь идет о литералах рассуждения, то вопрос об их отрицаниях особых сложностей не вызывает. Если мы говорим «Не A» или «Невозможно A», где A является литералом, то подразумеваем дополнение соответствующего множества A в некотором универсуме. Более сложен ответ на вопрос, что является с точки зрения E‑структур отрицанием данного суждения. И тем более непростой является математическая модель отрицания для рассуждения, содержащего связную совокупность суждений. Рассмотрим
сначала, как решается вопрос с отрицаниями в математической логике. Язык
математической логики подчиняется строгим законам синтаксиса. Эти, по правде
сказать, не очень простые для изучения законы нам для понимания дальнейшего
изложения знать необязательно. Важно то, что весь разнообразный и необозримый
набор синтаксически правильных предложений, выраженных на языке математической
логики, можно представить как множество формул. Формулы могут быть простыми и
сложными, но для каждой формулы существует единственное отрицание, которое
выражается с помощью приписывания логической связки «не» перед формулой.
Например, если исходная формула у нас обозначена как F, то ее отрицанием
является формула, которая обозначается как ØF (или в некоторых
источниках как 1)
формула F Ù 2)
формула F Ú Здесь у нас знаками Ù и Ú обозначены соответственно логические связки "И" (конъюнкция) и "ИЛИ" (дизъюнкция). Эти законы имеют в логике соответствующие названия: закон непротиворечия и закон исключенного третьего, и они к тому же однозначно определяют свойства отрицания. Из них, в частности, следует, что для любой формулы может быть только одно отрицание. С учетом этих законов нетрудно увидеть сходство между отрицаниями в математической логике и дополнениями в алгебре множеств. В алгебре множеств соответствующие законы выражены для произвольного множества S в виде двух соотношений: S
Ç Здесь у нас пустое множество соответствует в логике безусловно ложному утверждению, а в случае, когда соответствующее множество равно универсуму, это означает, что соответствующее логическое выражение безусловно истинно. Чтобы найти более тесную связь между логикой и алгеброй множеств, рассмотрим понятие «подстановка» в математической логике. Обычно каждая формула содержит определенное число переменных, вместо которых можно подставить какие-то константы (например, переменной может быть "книга в библиотеке", а константой – какая-то конкретная книга). Если в формуле одна или несколько переменных, и все эти переменные заменяются константами, то совокупность этих констант и их соотнесенность с соответствующими переменными называется подстановкой данной формулы. Если данная подстановка характеризуется тем, что формула, в которой все переменные заменены соответствующими константами, является истинной формулой, то такая подстановка называется выполняющей подстановкой данной формулы. При интерпретации формул математической логики, когда мы рассматриваем каждую логическую формулу как множество выполняющих подстановок, оказывается, что отрицание формулы полностью соответствует дополнению алгебры множеств. Например, логическая формула выражает понятие "множество пар всех целых чисел X и Y, сумма которых равна 100". Тогда при выборе соответствующего универсума, например, "множество всех пар целых чисел", отрицанием этой формулы будет понятие "множество всех таких пар, сумма которых не равна 100". При таких условиях подстановка (это означает, что X = 34, а Y = 66) в нашу формулу будет выполняющей подстановкой, а подстановка - нет. Т.е. для формул с несколькими переменными выполняющие подстановки можно представить как некоторые последовательности (или кортежи) из элементов, а саму формулу как множество таких кортежей. Рассмотрим это соответствие более подробно. Представим алгебру множеств, элементами которой являются всевозможные подстановки для заданной в формуле совокупности переменных. Таких подстановок может быть бесконечное число (например, когда областью значений хотя бы одной переменной является бесконечный натуральный ряд чисел), но суть от этого не меняется. Каждую формулу, содержащую заданное множество переменных, можно представить как некоторое множество выполняющих подстановок для этих переменных. Тогда безусловно ложная формула в этом случае означает формулу, для которой выполняющих подстановок не существует (например, формула выражающая понятие "множество всех простых чисел, последней цифрой которых является 6"), а формула, в которой любая подстановка является выполняющей подстановкой, и которая в силу этого свойства является тавтологией или теоремой, соответствует универсуму этой алгебры множеств. Соответственно отрицание заданной формулы означает формулу, в которой выполняющими подстановками являются всевозможные элементы нашего универсума, которые не являются выполняющими подстановками исходной формулы. Так что связь формул математической логики с законами алгебры множеств очевидна: произвольная формула соответствует некоторому подмножеству универсума подстановок, которые для нее являются выполняющими, безусловно ложная формула – пустому множеству выполняющих подстановок, а тавтология или теорема – универсуму. При переходе к E-структурам возникает проблема соответствующей интерпретации. Если в математической логике отрицание формулы также является формулой, то в E‑структурах формальное отрицание, т.е. присоединение знака отрицания или дополнения к соответствующей E-структуре или к отдельному суждению, не является суждением. Например, формальным отрицанием суждения «Все улитки молчаливы» будет предложение «Неверно, что все улитки молчаливы». Это предложение можно выразить в виде формулы исчисления предикатов, но оно по форме не является суждением E-структуры. На самом деле в этом случае отрицанием будет не одно, а некоторое множество суждений. В современной логике с некоторых пор стали много внимания уделять "неклассическим" логикам, в которых в той или иной степени не соблюдаются законы классической логики. Среди них весьма распространены логики, у которых для одной формулы допускается не одно, а большее число различных отрицаний. Мотивы такой тенденции вроде бы понятны. Например, суждение "Всем A не присуще B" вроде бы "отрицает" суждение "Всем A присуще B", но в строгом смысле отрицанием не является, так как оно не эквивалентно правильному отрицанию "Неверно, что всем A присуще B". Это отрицание не только включает в себя суждение "Всем A не присуще B", но и такие, как "Некоторым A не присуще B" и "Всем не A присуще B". Некоторые специалисты по логике (к ним относится и автор данной работы) считают, что использование понятия "отрицание" для обозначения разных сущностей вносит ненужную путаницу в логику. Чтобы избежать этой неоднозначности, будем различать отрицания и антитезы. Смысл отрицания при этом остается прежним, т.е. в полном соответствии с законами классической логики. Антитезой суждения будем называть такое суждение, которое при соединении с первоначальным суждением вызывает коллизию парадокса. Например, если у нас исходным суждением является предложение «Все жирафы – хищники», то в этом случае его антитезой является суждение «Все жирафы – не хищники», поскольку (в этом нетрудно убедиться) при совмещении этих двух суждений появляется коллизия парадокса «Все жирафы – не жирафы». Тогда известные в традиционной логике контрарные и контрадикторные суждения (см. разделы 6 и 8) являются антитезами в этом смысле. Но для E‑структур при таком подходе можно сформулировать намного более широкий набор всевозможных антитез. С точки зрения алгебры множеств антитеза имеет следующие свойства. Пусть F некоторое логическое выражение (или формула), которое можно рассматривать как множество выполняющих подстановок из универсума U. Обозначим Anti(F) антитезу F. Ее тоже можно интерпретировать как множество выполняющих подстановок в универсуме U. Тогда будут справедливы следующие соотношения: 1)
F Ç Anti(F) = Æ; 2) F È Anti(F) ¹ U; 3) Anti(F) Ì Из этих соотношений хорошо видно сходство и отличие антитезы и отрицания (дополнения). Простейшим примером антитезы является отношение "больше" применительно к "меньше". В то же время строгим отрицанием отношения "меньше" является отношение "больше или равно". И хотя отношение "больше" в строгом смысле не является отрицанием "меньше", тем не менее применительно к каким-либо фиксированным объектам оно несовместимо с ним. Многие антонимы в естественном языке, такие как "молодой — старый", "красивый безобразный", с точки зрения математической логики также не являются отрицаниями друг друга и относятся к классу антитез. Если же речь идет о суждениях, то контрарные и контрадикторные суждения, о которых шла речь в разделах 6 и 8, являются антитезами исходных. В то же время с точки зрения математической логики они не являются их отрицаниями. Если
при формулировке антитез использовать только базовые литералы, то множество
всех возможных базовых антитез легко находится с помощью CT-замыкания исходной
структуры. Рассмотрим сначала простейший случай, когда E-структура содержит
единственное суждение, например, A®B. Тогда для этой
структуры можно построить две антитезы: A® Можно легко доказать, что добавление любого из этих суждений-антитез в E-структуру инициирует коллизию парадокса. Антитезы часто используются в полемике. В естественных рассуждениях контраргументы (или контрдоводы) нередко формулируются как антитезы. Если в рассуждении присутствует в качестве посылки или в качестве следствия какое-либо суждение K, то контраргументом в этом случае является не вызывающее сомнений суждение, являющееся антитезой K. Если нашу антитезу невозможно опровергнуть, то можно считать, что мы переспорили оппонента тчательно используя при этом индукцию и абдукцию. В философии и логике считается, что индукция и абдукция – это более высокие по сравнению с дедукцией формы мышления, непосредственно связанные с творческим мышлением, т.е. с мышлением, результатом которого являются новые знания. Но в современной логике отсутствует однозначное определение абдукции. Считается, что абдуктивные выводы были предложены одним из создателей математической логики Ч. Пирсом. Исследуя теорию силлогистики Аристотеля, он предложил модифицировать ее, чтобы получать не только дедуктивные выводы, но и правдоподобные рассуждения. Рассмотрим в качестве примера один из силлогизмов Л. Кэрролла. Даны посылки: 1) Все молчаливые существа не забавны; 2) Все улитки молчаливы. Если использовать правила силлогистики, то получим следствие: Все улитки не забавны. Это же следствие можно легко получить и с помощью E-структур. Из схемы этого силлогизма Пирс построил два других типа рассуждения. Одно из них он назвал принятием гипотезы, а позже предложил назвать "абдукцией". Вот это рассуждение. Исходная посылка: Все улитки молчаливы. Получен результат: Все улитки не забавны. Далее рассуждаем так: чтобы этот результат был следствием исходной посылки, необходимо в состав посылок добавить гипотезу "Все улитки молчаливы". Поиск такой посылки как раз и есть абдуктивный вывод. Для простого силлогизма подобная схема рассуждения была известна намного раньше исследований Ч. Пирса, но она имеет другое название – энтимема, т.е. рассуждение с пропущенной посылкой. Рассмотрим подробно известный пример. Дано рассуждение «Этот человек не знает дорогу к реке. Следовательно, он не местный житель». Это по сути силлогизм с пропущенной посылкой. Для его анализа используем E‑структуры. Введем
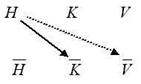
обозначения: H – этот человек, K – знающий дорогу к реке, V – местный житель.
Исходной посылкой является связь H®
Рис. 1 Следуя Ч. Пирсу, будем называть абдукцией методы анализа рассуждений, в которых требуется найти подходящую гипотезу для того, чтобы построить корректную логическую связь между исходными посылками и предполагаемым следствием из этих посылок. В отличие от энтимемы абдукция используется в более сложных, чем простой силлогизм, случаях. Абдукция встречается не только в научном анализе, но и во многих других мыслительных актах, даже в такой, казалось бы, далекой от логики сфере как юмор. В качестве примера проанализируем один анекдот, связанный с известным британским политиком Уинстоном Черчиллем. Как известно, он прекрасно разбирался в тонкостях языка (ему, кстати, была присуждена Нобелевская премия по литературе за мемуары о Второй мировой войне), и его остроты далеко не всем приходились по вкусу. Однажды чем-то обиженная на него леди Астор сказала ему: «Если бы вы были моим мужем, я бы подсыпала вам яд в кофе». Черчилль тут же ответил: «Если бы вы были моей женой, то я бы этот кофе выпил». Смешное обычно не принято комментировать. Но здесь иная ситуация – ставится задача найти связь комического с абдукцией. Ответ Черчилля внешне безобиден. Однако при этом "домысливается", что его ответу должна предшествовать фраза «А вы мне так неприятны, что... » и предпосылка о том, что в моделируемой ситуации говорящий знает о насыпанном яде. Эти недостающие звенья являются абдуктивным выводом из произнесенных фраз и ситуации, и смех (по крайней мере, у людей с чувством юмора) вызывает не только этот скрытый намек, но и не в последнюю очередь радость, связанная с его самостоятельной и быстрой «расшифровкой». Алгоритм поиска абдуктивных выводов. Даны исходные посылки и предполагаемое следствие, допустим, P®Q. Тогда выполняются следующие действия: Шаг 1. Построить структуру с исходными посылками и затем вывести контрапозиции к каждой из посылок. Шаг 2. Проверить существование в полученной структуре пути из P в Q. Если такого пути нет, то переход к шагу 3, иначе выход из алгоритма с ответом "Для данной задачи абдуктивный вывод не требуется". Шаг 3. Используя построенную на шаге 1 структуру, построить верхний конус PD и нижний конус QÑ. Шаг 4. Из полученных на шаге 4 множеств записать все возможные пары (Xi, Yj), где XiÎPD и YjÎQÑ. Шаг 5. Для каждой пары, полученной на шаге 4, проверить, используя теорему корректность гипотезы Xi,®Yj. Если гипотеза некорректна, то соответствующая пара исключается из списка. Оставшиеся пары являются возможными вариантами ответа. Конец алгоритма. Неформальное пояснение к алгоритму. С помощью этого алгоритма мы ищем недостающие звенья цепи P®... ®Q, так как разрывы в этой цепи означают, что суждение P®Q не является следствием исходных посылок. Список пар, полученных на шаге 4, является полным списком этих недостающих звеньев, т.е. гипотез. Но некоторые из них могут быть некорректными, поэтому необходим шаг 5. Рассмотрим, как работает этот алгоритм применительно к нашей задаче. Шаг 1 и Шаг 2 уже выполнены. Шаг 3. Из рисунка 50 получаем AD = {A, B, Шаг 4. Список возможных пар: (A,
Шаг
5. Из этого списка сразу можно исключить пары (A, Для гипотезы A®C: AÑ = {A}; CD= {C, гипотеза некорректна. Для
гипотезы A® AÑ = {A}; гипотеза корректна. Проверив остальные гипотезы, мы убедимся, что возможными вариантами абдуктивного вывода для данной задачи могут быть только следующие базовые суждения: A® Какой из этих вариантов самый подходящий, можно решить только на основе содержательного анализа. Каждая новая связь влечет за собой некоторую совокупность новых следствий. Некоторые из них могут оказаться несовместимыми с какими-то явно невыраженными, но подразумеваемыми правильными суждениями. Если и на этом этапе все наши абдуктивные выводы будут забракованы, то можно остановиться на том, что предполагаемое следствие в данной системе необходимо принять в качестве исходной посылки при условии, что его добавление в структуру не вызывает коллизий. Рассмотренный метод допускает также реализацию, в которой абдуктивные выводы могут содержать термины, не входящие в первоначальную структуру, т.е. когда в качестве гипотез выбираются не базовые, а частные суждения. В приведенном выше анекдоте именно эта ситуация. Необходимо отметить, что анализ рассуждений на основе E-структур характеризуется намного более широкими возможностями, чем методы анализа на основе силлогистики Аристотеля и полисиллогистики. В частности, методы силлогистики не позволяют исследовать возможные гипотезы, проверять правильность рассуждения с помощью анализа коллизий, находить возможные абдуктивные выводы. В то же время в E-структурах имеются четкие алгоритмы для реализации этих видов анализа рассуждений. Такие новые возможности анализа появляются за счет использования в качестве моделей рассуждений сугубо математических структур, таких, как алгебра множеств, теория графов, теория частично упорядоченных множеств. Синтезом этих математических структур являются E-структуры. Список литературы 1. Кэрролл Л. История с узелками. - М.: Мир, 1973. 2. Кулик Б.А. Моделирование рассуждений на основе законов алгебры множеств // Труды V национальной конференции по искусственному интеллекту. Казань, 7-12 октября 2006 г. Т.1. С. 58-61. |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |