|
Дипломная работа: Исследование фазовых эффектов в бинарных азеотропных смесяхДипломная работа: Исследование фазовых эффектов в бинарных азеотропных смесяхМинистерство образования и науки Российской Федерации МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ТОНКОЙ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ им. М.В. Ломоносова Кафедра химии и технологииосновного органического синтезаАттестационная работа по теме: «Исследование фазовых эффектов в бинарных азеотропных смесях»на соискание степени бакалавра по направлению 550800 «Химическая технология и биотехнология» Москва 2004Оглавление Введение………………………………………………………….……………….3 1. Литературный обзор…………………………………………………………...3 1.1.Диаграммы объем-состав пара; состав жидкости и энтропия-состав пара, состав жидкости…………………………………………………………………..3 1.2.Вид изотермо-изобар в бинарных смесях…………………………………..6 1.3.Некоторые понятия физико-химического анализа………………………....7 1.4.Определение ноды как вектора…………………………………………….11 1.5.Выбор направления ноды и реноды……………………………….……….12 1.6.Изменение концентрации фаз при фазовом обмене при постоянной температуре и давлении………………………………………………………...13 1.7.Общие фазовые эффекты…………………………………………………...16 1.8.Цель работы……………………………………………………….…………18 2. Частные фазовые эффекты и вывод уравнения Ван-дер-Ваальса………..19 2.1.Вывод основных уравнений для частных фазовых эффектов жидкой и паровой фаз при постоянной температуре и давлении ....19 2.2.Вывод уравнений Ван-дер-Ваальса для жидкой и паровой фаз…..……26 3. Фазовые эффекты и уравнение Ван-дер-Ваальса для бинарных азеотропных смесей………………………..…………………………………..30 3.1. Фазовые эффекты в бинарных азеотропных смесях……………………..30 3.2. Фазовые эффекты в гетероазеотропных смесях…………...………...45 3.3.Уравнение Ван-дер-Ваальса в терминах общих и частных фазовых эффектов…………………………………………………….…………………...51 4. Заключение……………………………………………………………………51 Список использованной литературы…………………………………………..52 Обозначения…………………………………………………………………......54 Введение. Уравнение Ван-дер-Ваальса используется при исследовании процессов разделения и является базовым уравнением при качественном исследовании этих процессов. Распространение уравнения такого типа на многокомпонентные смеси осуществлено А.В. Сторонкиным. Вместе с тем, для понимания всех тонкостей уравнения Ван-дер-Ваальса-Сторонкина необходимо изучить уравнение Ван-дер-Ваальса, которое было получено для бинарных смесей. Уравнение Ван-дер-Ваальса тесно связано с уравнениями так называемых фазовых эффектов. А. В. Сторонкиным рассмотрены фазовые эффекты, использующие химические потенциалы. В рукописных материалах Л. А. Серафимова введено понятие общих и частных фазовых эффектов. Данное исследование посвящено анализу в азеотропных смесях взаимосвязи фазовых эффектов с уравнением Ван-дер-Ваальса. 1. Литературный обзор.1.1.Диаграммы объем-состав пара, состав жидкости и энтропия-состав пара, состав жидкости В бинарных двухфазных системах в общем случае составы фаз неодинаковы. В связи с этим при взаимных превращениях фаз, т.е. в условиях массопереноса веществ из одной фазы в другую фазу происходит изменение их состава и других параметров как экстенсивных, так и интенсивных. К интенсивным параметрам относят температуру, давление и химические потенциалы компонентов. К экстенсивным – все термодинамические функции, такие как внутренняя энергия, энтальпия, функция Гиббса, а также количество вещества. Для учета влияния изменения состава фаз в результате их взаимного превращения на их состояние А.В. Сторонкиным и М.И. Шульцем было введено понятие изобарно-изотермических фазовых эффектов [1]. Изобарно-изотермический фазовый эффект возникает каждый раз, когда массоперенос рассматривается при постоянной температуре и давлении. Осуществить массоперенос такого типа в двухфазной системе, например жидкость-пар или жидкость-жидкость практически невозможно. Эти процессы протекают обычно или при постоянном давлении или при постоянной температуре. Как известно двухфазная многокомпонентная система имеет число степеней свободы определяемое уравнением: f=n-Ф+2=n, Ф=2 1.1 Если закреплены давление и температура, т.е. P=const и T=const, то f=0, то есть, в параметрическом пространстве состояний такая система характеризуется точкой. Таким образом, закрепление давления и температуры однозначно определяет состав двухфазной бинарной смеси и, следовательно, в данном случае не может быть никаких изменений за счет фазовых процессов. Поэтому в бинарных смесях изобарно-изотермический фазовый эффект несовместим с фазовым равновесием. Рассмотрим вопрос подробней. Как известно, фазовое равновесие определяется следующим набором равенств, в случае бинарной смеси Рп = Рж Тп = Тж 1.2 µп1 = µж1 µп2 = µж2 Если закреплены давление и температура, то химические потенциалы первого и второго компонента должны быть постоянными, так как исчерпаны степени свободы. Следовательно, постоянными будут и составы равновесных фаз. Поэтому в рассматриваемом случае изобарно-изотермический фазовый эффект считается не процессом, а свойством двухфазной системы, которое выражается специфическим образом. Состояние компонентов в фазах характеризуется при постоянном давлении и температуре их химическими потенциалами µ1 и µ2. Будем различать фазовые эффекты общего типа, которые связаны с химическими потенциалами и фазовые эффекты частного типа, которые связаны с экстенсивными функциями. Обычно фазовые эффекты относят к той или иной фазе двухфазной системы. На рисунке 1.1 изображены исследуемые диаграммы зеотропных смесей при T=соnst и Р=соnst.
V2оп пар S2оп пар V1оп S1оп
V2ож S2ож S1ож V1ож
жидкость жидкость х1 у1 х1,у1 х1 у1 х1,у1 a) б)Рис.1.1. Диаграммы а) V - х, у, Т=const и б) S - х, у, Р=constВся диаграмма в этом случае имеет три области: область перегретого пара, область гетерогенности и область переохлажденной жидкости. Область пара от гетерогенной области отделена линией насыщенного пара, гетерогенная область отделена от области жидкости линией кипящей жидкости. В гетерогенной области проведены конноды жидкость-пар отрезки, соединяющие состояние жидкости и пара. При Т=соnst равновесные составы имеют одинаковое давление и химические потенциалы компонентов, при Р=соnst равновесные составы имеют одинаковую температуру и одинаковые химические потенциалы компонентов. Конноды, как изотермо-изобары гетерогенной части, имеют после точек излома продолжение в областях пара и жидкости. Вдоль конноды жидкость-пар химические потенциалы не изменяются, а изменяется (скачком) объем и энтропия от Vж к Vп и от Sж к Sп. Вдоль же изотермо-изобар, так как давление и температура постоянны, справедливо уравнение Гиббса-Дюгема: x1 dμ1ж+ x2 dμ2ж=0, y1 dμ1п+ y2 dμ2п=0. 1.3 т.е. химические потенциалы не постоянны. 1.2.Вид изотермо-изобар в бинарных смесях. Образование раствора при постоянном давлении и температуре сопровождается повышением энтропии Sм и понижением Gм потенциала, при этом [2, 3]: Hм=T Sм + Gм 1.4 Так как величина G при смешении меньше по сравнению с величиной, определяемой по аддитивности, а величина S больше по значению с величиной, определяемой по аддитивности, то различие между ними есть тепловыделение|T Sм| < |Gм| 1.5или теплопоглощение |T Sм| > |Gм| 1.6 Учитывая, что H - G >0, изотермо-изобара всегда обращена выпуклостью вверх, т.е. в бинарной смеси
Это можно объяснить следующим образом. Так как температура кипения легколетучего компонента меньше температуры кипения тяжелолетучего компонента, то изотермо-изобара будет иметь на диаграмме S - x, y тангенс угла наклона положительный вдоль абсциссы x1. Эти свойства изотермо-изобары в бинарной смеси не зависят от того, рассматривается жидкая фаза или паровая. Однако эта кривизна изотермо-изобар очень мала, так как мала энтропия образования раствора. В качестве примера: энтропия образования 0,5 мольного раствора (х=0,5) идеальной смеси, т.е. максимальная энтропия образования равна: -R(x1lnx1+x2lnx2)= - R lnx1= -1,98· ln 0,5 =1,3724 кал/(моль К). Что касается объема, то объем вдоль изотермо-изобары может уменьшаться, увеличиваться или на одном участке увеличиваться, а на другом уменьшаться. Но это уменьшение или увеличение незначительно по сравнению с величиной объема пара. Поэтому в общем случае вдоль изотермо-изобар жидкости и пара, энтропию и объем можно принять линейно-зависимыми от состава. 1.3. Некоторые понятия физико-химического анализа. Коннодой называется отрезок, соединяющий два состояния двухфазной системы. Векторы состояния: < V(1) S(1) x(1)1 x(1)2 x(1)3 … x(1)n-1> и <V(2) S(2) x(2)1 x(2)2 x(2)3 x(2)n-1>. Верхний индекс относится к фазам в двухфазной системе. В двухфазной системе имеем фазу с большим объемом и энтропией и фазу с меньшим объемом и энтропией, мы получим конноду, если от вектора состояния с большим объемом и энтропией отнимем вектор состояния фазы с меньшим объемом и энтропией. Элементы векторов состояния есть проекции этих векторов на оси координат. Вектор, обратный конноде, есть реконнода. Приставка ре- означает обратное действие. Понятия «коннода» и «реконнода» относятся к двухфазным системам. Проекции конноды на ось состава образуют ноду и реноду. Если же имеет место многофазная система, то фигура, соединяющая состояния каждой фазы носит название гиперконноды [5]. Гиперконнода имеет вид симплекса, число вершин которого равно числу фаз. Проекции на ось состава есть три ноды. Понятия «коннода» и «нода» использует Финдлей в своей монографии. Имеется перевод на русский язык под редакцией А.В. Раковского 1935г. [4]. Понятие гиперконноды, введено в монографии Л.С. Палатника, А.И. Ландау [5]. В этой монографии также активно используется понятие конноды. На рисунке 1.3 изображена гиперконнода. Остановимся на понятии «нода». В латинском языке node- узел. В английском node означает: в ботанике узел, в физике и философии - узловой шунт, в медицине - нарост, уплотнение и узловое соединение, астральная точка, пересечение орбит. В математике - точка пересечения двух линий (кривых или прямых). Nodal – центральный, узловой. Nodus - узел, затруднение, сложное сплетение обстоятельств (интриги). Con- приставка означает связь, konjgtium - соединение, сопряженное объединение (conjunct- соединенный). Отметим, что ноды и конноды связывают различные состояния и составы фаз, находящихся в равновесии. Но в равновесии Р(1) = Р(2) =…= Р(m) Т(1) = Т(2) =…= Т(m) µ(1)1 = µ(2)1 = …= µ(m)1 1.9 µ(1)2 = µ(2)2 =…= µ(m)2 ………………… µ(1)n= µ(2)n=…=µ(m)n Таким образом, если в качестве переменных выбраны интенсивные параметры, то в этих координатах равновесные состояния фаз соответствуют одной точке, что отражается в рассмотренном выше понятии «узел». Выбор экстенсивных параметров в качестве переменных дает ноду, конноду, гиперконноду. В [6,7] использовано понятие нод. В [8] вместо ноды используется понятие «соединительная линия». Очень неудачное понятие. Во-первых, не линия, а отрезок, а во-вторых, как быть, когда система многофазна? Введение нами в дальнейшем направленного отрезка, т.е. отождествления ноды и конноды с векторами, требует введения понятия реконноды и реноды. Для трех фаз можно использовать понятие векторов. Из трех фаз одна фаза с наинизшей энтропией и объемом, другая фаза с промежуточными значениями и, наконец, с наивысшими значениями (рис.1.4). В [4] на стр.251 приводится следующее определение: «Прямые, соединяющие точки жидкости и пара, находящиеся в равновесии при Т=const в диаграмме V-x¸y называются нодами (или коннодами)» (рис. 1.5). Рассмотрено, что коннода жидкость-пар для зеотропных смесей вертикальна по отношению к оси состава[4]. В 1924г вышла книга Партингтона на английском языке ²Chemical an introduction to general thermodynamics and its application to chemistry² [9]. Ранее, в 1913г. вышла книга этого же автора: “Text book of thermodynamics with special reference to Chemistry”. Курс Партингтона, изданный в 1924г., был первым курсом, излагающим не собственные идеи, а главнейшие методы химической термодинамики в доступной форме. В [10] также упоминается понятие конноды (стр. 49, 121, 125, 299, 504). Там пишут: «Если на диаграмме имеются две точки, изображающие фазы, находящиеся в равновесии, то, соединив эти точки прямой, получают отрезок, называемый коннодой или нодой». Далее коннодами являются отрезки соединяющие составы (состояния) в диаграммах Т - х, у. Гиперконнода является треугольником коннод (трехфазный треугольник). Прямые, соединяющие две жидкие фазы, лежащие на бинодальной кривой, многие авторы называют нодами. Вместе с тем в [11] на стр. 552 в разделе ²Эктракция² горизонтальные линии, соединяющие насыщенные растворы в диаграммах Т-х, названы коннодами (иногда их называют нодами) или хордами равновесия. Кривая, соединяющая концы коннод - бинодаль (рис.1.6). Мы считаем название «хорда» неудачным. В [12] активно используется понятие нода. В трудах Гиббса отсутствует понятие конноды и ноды [13]. Таким образом, понятие конноды и ноды было введено между 1900 и 1913 годом. Понятие гиперконноды введено в 1961 году. 1.4.Определение ноды как вектора. Уравнение для потенциала получают путем покоординатного преобразования Лежандра фундаментального уравнения [14, 15], при этом знак преобразованной координаты меняется на противоположный. Поэтому, осуществив преобразование Лежандра относительно всех составляющих фундаментального уравнения, мы получим уравнение нулевого потенциала вида: -S dT + VdР – x1 dμ1 – x2 dμ2-…- xn dμn=0 1.10 Обычно в литературе приводят уравнение нулевого потенциала с измененными на обратные знаками. Учитывая, что справа стоит нуль, это, вероятно, правомерно. Коннода (отрезок, соединяющий функции состояния системы), полученная из уравнения 1.10, есть разность между уравнениями этой системы. Как графически изобразить эту разность? Все определяется выбором начальной и конечной точек вектора, которому соответствует коннода. Если мы за начало отсчета выберем жидкую фазу, желая изучить изменение ее состояния, то согласно уравнению 1.10 получим: (Sп- Sж) dT –(Vп-Vж) dР+ (y1- x1) dμ1 + (y2- x2) dμ2+…+(yn- xn) dμn=0 1.11 Уравнение 1.11 есть скалярное произведение вектора конноды на вектор параметров. Вектор коннода: <Sп- Sж, Vп-Vж, y1- x1, y2- x2 ,…yn- xn>. Вектор параметров: <dT, dР, dμ1, dμ2, dμn>. Если же мы изучаем изменение состояния в паровой фазе, то резонно за начало отсчета выбрать свойства паровой фазы, т.е. получить реконноды: (Sж- Sп) dT –(Vж-Vп) dР+ (x1- y1) dμ1 + (x2- y2) dμ2+…+(xn- yn) dμn=0 1.12 1.5.Выбор направления ноды и реноды. Нода - это отрезок, соединяющий составы равновесных фаз в двухфазных системах. Ренода – отрезок, ориентированный противоположно. Коннода – это отрезок, соединяющий функции состояния системы. К этим функциям относятся экстенсивные величины: объем, энтропия и составы фаз двухфазной системы. Реконнода отрезок, ориентированный противоположно конноде. Запишем нулевой потенциал Гиббса для двухфазной системы жидкость-пар: Sж dT –Vж dР+ x1 dμ1 + x2 dμ2+…+xn dμn=0 1.13 Sп dT –Vп dР+ y1 dμ1 + y2 dμ2+…+yn dμn=0 Условие равновесия фаз определяется следующими равенствами:Рж=Рп Тж=Тп μ1ж= μ1п 1.14 μ2ж= μ2п ……… μnж= μnп В связи с этим верхние индексы в уравнениях нулевого потенциала опущены. Рассмотрим знаки при элементах нулевого потенциала. Фундаментальное энергетическое уравнение имеет вид: dU = Т dS - P dV + μ1 dx1+ μ2 dx2 +…+ μn dxn 1.15 Отметим, что в общем случае направление конноды определяет направление ноды, а направление реконоды определяет направление реноды. Если же за основу мы возьмем уравнение 1.13, то очевидно получим уравнение конноды: <-(Sп- Sж) dT +(Vп-Vж) dР - (y1- x1) dμ1 - (y2- x2) dμ2-…-(yn- xn) dμn> 1.16 и уравнение реконноды:<- (Sж- Sп) dT +(Vж-Vп) dР - (x1- y1) dμ1 - (x2- y2) dμ2-…-(xn- yn) dμn> 1.17 Аналогично выглядят векторы ноды в этом случае (когда используется уравнение 1.13) ноды < y1- x1, y2- x2,…yn- xn> 1.18 реноды < x1- y1, x2- y2,… xn- yn> Когда используется уравнение 1.10 ноды < x1- y1, x2- y2,… xn- yn> 1.19 реноды < y1- x1, y2- x2,…yn- xn> В рассмотренных случаях, т.е., когда за основу берется уравнение 1.13 и уравнение 1.10, ориентации векторов получаются противоположные. 1.6. Изменение концентрации фаз при фазовом обмене при постоянной температуре и давлении. Рассмотрим изменение концентрации компонента i в жидкой фазе в зависимости от того, приходит dm молей паровой фазы в жидкую или уходит dm молей паровой фазы из жидкой. Здесь существует два способа вывода уравнений. 1. Бесконечно малое количество компонента i может быть выражено двояко: с одной стороны [16] dmi = d(m xi) 1.20 с другой стороны dmi= yidm 1.21 приравняв эти выражения, получаем: d(m xi) = yidm 1.22 т.е. m dxi+ xi dm = yidm 1.23 m dxi = (yi -xi) dm или Допустим i=1 Ki>1, тогда yi >xi dt>0, dxi>0 dt<0, dxi<0 если i=2 Ki<1, yi <xi dt>0, dxi<0 dt<0, dxi>0 2. Второй способ изложен в [17] Для систем испарения: m xi =(m-dm)( xi -dxi) + yi dm 1.25 m xi = m xi -m dxi- xi dm + dm dxi + yi dm после отбрасывания бесконечно малых второго порядка имеем: m dxi=( yi -xi)dm
Если же идет конденсация dm молей пара в жидкость, имеем: yi dm + m xi = (m+dm)( xi +dxi) 1.26 или yi dm + m xi = m xi + m dxi +xi dm + dm dxi dm (yi - xi) = m dxi 1.27
Обоими методами мы получили один и тот же результат, а именно: если рассматривается изменение состояния жидкой фазы, используется нода, а не ренода. Теперь рассмотрим изменение концентрации компонента i в паровой фазе, в зависимости от того, приходит ли dm молей состава xi из паровой фазы. Здесь также существует два метода вывода уравнений: 1. Для систем испарения: xi dm= d(m yi) 1.29 xi dm= yi dm + m dyi 1.30 dm (xi- yi) = m dyi 1.31 или 2. Для систем конденсации: m yi =(m-dm)( yi -dyi) + xi dm 1.33 m yi = m yi -m dyi- yi dm + dm dyi + xi dm после отбрасывания бесконечно малых второго порядка имеем m dyi=(xi -yi)dm 1.34 или Для систем смешения (с dt>0) m yi + xi dm = (m+dm)( yi +dyi) 1.36 m yi + xi dm = m yi + m dyi-+ yi dm + dm dyi 1.37 dm (xi- yi ) = m dyi 1.38
Второй метод более громоздок. Каждый вывод предусматривает dt>0 или dt<0. Первый метод более универсален и лаконичен. Основной вывод заключается в том, что при исследовании изменения концентраций за счет добавления или удаления из данной фазы dm молей состава другой фазы, для жидкой фазы используется нода, а для паровой фазы - ренода. Это правило действует в случае балансовых соотношений. 1.7. Общие фазовые эффекты. Общие фазовые эффекты отражают изменение химических потенциалов компонентов при изменении их концентрации за счет фазового обмена [1]. Рассмотрим m молей жидкой фазы и допустим, что пришло (или ушло) в нее dm молей состава паровой фазы. Как и прежде dt= dln m. Тогда при постоянном давлении и температуре имеет место:
но используя эти соотношения, из 1.40 и 1.41 получим:
Обозначив
получим
Таким образом, при y1>x1 , dt>0 dx1>0 y2<x2 , dt>0 dx2<0 Обычно говорят, что если
фазовый эффект Перейдем к фазовым эффектам в паровой фазе. Здесь
Но при приходе (или уходе) из паровой фазы dm молей состава жидкой фазы
Следовательно, из 1.48 и 1.49 окончательно получаем
Следовательно, при x1< y1, dt>0, dy1<0, x2> y2, dt>0, dy2>0, Таким образом, если Запишем уравнение фазовых эффектов в жидкой фазе. Так как сумма dx1+dx2=0, следовательно, dx1= -dx2 , а также у1-х1= -(у2-х2), получаем: но Аналогично можно получить Таким образом, были получены общие фазовые эффекты. В случае азеотропных смесей при y1 = x1 очевидно σ1 – σ2 = 0, при этом σ1 = 0 и σ2 = 0. Таким образом, в случае азеотропных смесей общие фазовые эффекты равны нулю, в отличие от зеотропных смесей, где они отличаются от нуля. 1.8. Цель работы Получение и анализ новой формы уравнения Ван-дер-Ваальса на примере азеотропных смесей с использованием общих и частных фазовых эффектов. 2. Частные фазовые эффекты и вывод уравнения Ван-дер-Ваальса. 2.1. Вывод основных уравнений для частных фазовых эффектов жидкой и паровой фаз при постоянной температуре и давлении. Проведем вывод, используя диаграммы зеотропных смесей. На рис. 2.1 представлена зависимость V – x, y из [18] Любой материальный баланс линеен, в том смысле, что участвующие в нем два потока разных составов лежат на одной прямой с потоком, из которого они образованы. В случае, когда
температура постоянна, а давление является функцией состава, вектор Приход или уход dm молей из жидкости приводит к изменению, как её состава, так и её количества. С одной стороны бесконечно малое количество ушедшего или пришедшего в жидкость вещества (компонента i) равно d(mxi). С другой стороны это же количество можно выразить как yi dm. Очевидно d(mxi)= yi dm xi dm + m dxi= yi dm 2.1 m dxi=( yi - xi) dm
Очевидно, если dt>0, то dlnm>0 и вещество приходит в жидкую фазу, если dt<0, то dlnm<0 и вещество уходит из жидкой фазы. Физический смысл здесь ясен: если dt>0 количество жидкости увеличивается, а если dt<0 - уменьшается. Если индекс i равен 1, т.е. компонент легколетучий, имеем: y1> x1 dt<0 , то dх1<0 или y1> x1 dt>0 , то dх1>0 Таким образом, для легколетучего компонента, согласно физическому смыслу, если уходит dm молей состава пара, то уменьшается концентрация компонента 1 в жидкости, а если приходит, то увеличивается. Если же i=2 y2< x2 dt<0 , то dх2>0 y2< x2 dt>0 , то dх2<0 Для тяжелолетучего компонента, если уходит dm молей состава пара, то концентрация компонента 2 увеличивается в жидкости, а если приходит, то уменьшается. Вместе с тем, вектор
В обоих случаях векторы колинеарны, т.е. лежат на одной прямой, а их направления определяются знаком dt, как скалярного множителя (бесконечно малого). Возвращаясь к диаграмме (рис.2.1), в
случае постоянной температуры и переменного давления, вектор Таким образом, величина, определяющая
вектор 1. Проводим касательную к изотермо-изобаре жидкости в точке с координатами х1, Vж. 2. Пересечение этой прямой с прямой у1=const, дает вторую точку вектора (А). 3. Следовательно, вектор равен (см. рис. 2.1) Начальной точкой этого вектора
является точка с координатами х1, Vж. Конечной точкой является точка А. В самом
деле, если рассматривается коннода жидкость-пар (рис.2.3), то её координаты
равны Полученные результаты находятся в полном соответствии с физико-химическим смыслом. В самом деле, при dt<0 часть веществ уходит из жидкой фазы при постоянном давлении и температуре, следовательно, объем жидкой фазы уменьшается. При приходе dm молей в жидкую фазу объем жидкой фазы, в общем, увеличивается. Таим образом, для азеотропных смесей частные фазовые эффекты жидкой фазы противоположны по знаку частным фазовым эффектам паровой фазы. В отличие от общих они не равны нулю в азеотропных точках. 2.2.Вывод уравнений Ван-дер-Ваальса для жидкой и паровой фаз. Уравнение Ван-дер-Ваальса является представлением разности нулевых потенциалов Гиббса в координатах g-потенциала [14]. Напомним, что для жидкой фазы нулевой потенциал для бинарной смеси обычно записывается в форме [14] Sж dT –Vж dР+ x1 dμ1 + x2 dμ2=0 2.7 g-потенциал, соответственно, равен dgж= -Sж dT +Vж dР+ μ1dх1+ μ2 dх2 2.8 Аналогично для паровой фазы имеем Sп dT –Vп dР+ у1 dμ1 + у2 dμ2=0 2.9 dgп= -Sп dT +Vп dР+ μ1dу1+ μ2 dу2 2.10 В работе [14] дан вывод нулевого потенциала. Приведем его полностью. Для случая бинарной смеси уравнение внутренней энергии имеет вид: U= TS-PV+ μ1x1+ μ2x2 2.11 После дифференцирования получаем dU= TdS + SdT – PdV – VdP + μ1 dx1 + x1dμ1 + μ2 dx2 + x2dμ2 2.12 Но так как dU= TdS - PdV+ μ1 dx1 + μ2 dx2 2.13 то очевидно SdT-VdP+ x1dμ1+ x2dμ2 =0 2.14 Если применять почленно преобразование Лежандра, то, учитывая, что при этом меняется в каждом случае знак, получим -SdT+VdP- x1dμ1- x2dμ2 =0 2.15 Автор [14] не видит разницы между уравнениями в форме 2.14 и 2.15, поэтому приводит уравнение 2.15, очевидно считая, что если правая часть равна нулю, то обе формы идентичны. Как уже говорилось, нулевой потенциал есть скалярное произведение вектора < S, V, x1, x2 > на вектор < dT, dP, dμ1, dμ2 > Учитывая, что это скалярное произведение равно нулю, векторы-сомножители ортогональны друг другу. Так как, вектор < dT, dP, dμ1, dμ2 > есть вектор параметров, которые могут изменяться независимо, очевидно вектор < S, V, x1, x2 > может быть представлен двояко < S, -V, x1, x2 > или <- S, V, -x1, - x2 >
S х1 х2 х1 х -х2 х2 -х -S -х1 -х2 -х1 - S Рис.2.10. Взаимное расположение вектора состава То есть, в случае перемены знаков произведение знака не меняет, если давление постоянно. Выведем уравнение Ван-дер-Ваальса для жидкой фазы. Исходим из того, что в этом случае начальная точка вектора конноды при Р=соnst будет точка, соответствующая свойствам жидкой фазы. В связи с этим правилом запишем уравнения 2.14 для паровой и жидкой фаз при Р=соnst: Sп dT + у1 dμ1 + у2 dμ2=0 2.16 Sж dT + x1 dμ1 + x2 dμ2=0 2.17 Отнимем от первого уравнение второе и получим: (Sп- Sж) dT + (у1- х1)dμ1 +(у2- x2)dμ2=0 2.18 Таким образом, мы, получим произведение конноды жидкость-пар < Sп- Sж, у1- х1, у2- x2> на вектор параметров < dT, dμ1, dμ2 >, которые в условиях термодинамического равновесия одинаковы, как в жидкой, так и в паровой фазах. Так как х1+х2=1 и у1+у2=1, то очевидно у1- х1+ у2- x2=0 т.е. у2- x2= -(у1- х1) 2.19 Следовательно, с учетом 2.19 (Sп- Sж) dT + (у1- х1) (dμ1-dμ2)=0 2.20 В уравнении 2.20 dT и d(μ1-μ2) полные дифференциалы. Для перехода к координатам функции g необходимо выразить d(μ1-μ2), как функции х1 и Т (Р=соnst) d(μ1-μ2) = Подставляя в уравнение 2.20 значение d(μ1-μ2) из 2.21, получим
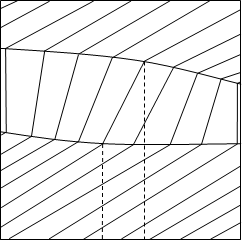
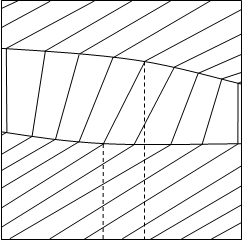
В связи с этим Таким образом, с учетом 2.23 и 2.24 окончательно получим - Аналогично можно получить для жидкой фазы уравнение при постоянной температуре и переменном давлении Учитывая, что нода для двухкомпонентной смеси определяется разностью концентраций одного из компонентов, уравнения 2.25 и 2.26 можно записать в форме и Отметим, что так как в азеотропных смесях коннода вертикальна, нода вырождается в точку. 3. Фазовые эффекты и уравнение Ван-дер-Ваальса для бинарных азеотропных смесей. Фазовые эффекты в бинарных азеотропных смесях. На рисунках 3.1 - 3.4
изображены диаграммы объем - состав фаз, и энтропия – состав фаз для азеотропа
с минимумом температуры кипения. Если рассматриваемый состав равен составу
азеотропа, а температура азеотропа минимальна, то уравнение Ван-дер-Ваальса
обращается в тождество 0 = 0. В этом случае изотермо-изобары жидкости и пара
обращены выпуклостью вверх. Нода (коннода) жидкость-пар направлена при составе
азеотропа вертикально, т. е. y1 - x1 = 0. Следовательно, на диаграммах частные фазовые эффекты
В паровой фазе Общий фазовый эффект в этом случае для жидкой фазы равен нулю, для паровой фазы также равен нулю, так как y1 = x1. В остальных случаях фазовые эффекты рассматриваются в двух областях: до точки азеотропа и после нее. Все изотермо-изобары жидкости обращены выпуклостью вверх. В связи с этим вдоль кривой, отделяющей гетерогенную область от гомогенной, в азеотропной точке изотермо-изобара для паровой фазы точечная, а для жидкости изотермо-изобара касается гетерогенной кривой в азеотропной точке. В азеотропной смеси изотермо-изобара совпадает с коннодой, соединяющей два состояния: паровое и жидкое. Проекция конноды на ось x, y есть нода. Изотермо-изобара в целом это ломаная. Для азеотропной смеси нода равна нулю. Любой материальный баланс линеен, в том смысле, что участвующие в нем два потока разных составов лежат на одной прямой с потоком, из которого они образованы. Рассмотрим область до точки азеотропа. В случае, когда
температура постоянна, а давление является функцией состава, вектор Если рассмотреть проекцию
вектора-ноды на ось x, y то получим для легколетучего компонента
y1>x1. Таким образом, в случае ухода dm молей пара из жидкости векторы Приход или уход dm молей из жидкости приводит к изменению как ее состава, так и ее количества. С одной стороны бесконечно малое количество ушедшего или пришедшего в жидкость вещества (компонента i) равно С другой стороны это же количество можно выразить так Очевидно xidm + mdxi = yidm mdxi = (yi xi) dm Очевидно, если dt >0 , то d(lnm) >0 и вещество приходит в жидкую фазу, если dt <0, то d(lnm) <0 – вещество уходит из жидкой фазы. Физический смысл здесь ясен. Если dt >0, количество жидкости увеличивается, а если dt <0 – уменьшается. Если i = 1, т. е. компонент легколетучий, имеем y1 > x1 dt >0, то dx1 >0 или y1 < x1 dt <0, то dx1 <0 Таким образом, для легколетучего компонента, согласно физическому смыслу, если уходит dm молей состава пара, то уменьшается концентрация компонента 1 в жидкости, а если приходит – увеличивается. Если же i = 2, то y2 < x2, dt <0, dx2 >0 y2 < x2, dt >0, dx2 <0 Для тяжелолетучего компонента, если уходит dm состава пара, то концентрация компонента 2 в жидкости увеличивается, а если приходит – уменьшается. Вместе с тем, вектор В обоих случаях векторы колинеарны, это значит лежат на одной прямой, а их знаки определяются знаком dt как скалярного множителя (бесконечно малого). Делаем вывод, что на
диаграмме (рис. 3.1) в случае постоянной температуры и переменного давления
вектор Величина, определяющая
вектор 1. Проводим касательную к изотермо-изобаре жидкости в точке x1, Vж. 2. Пересечение касательной с прямой y1 = const дает вторую точку вектора (т. А). 3.
Получаем вектор Начальной точкой этого вектора является точка с координатами (x1, Vж). Конечной точкой является точка А. Если рассматривается нода жидкость-пар, то ее координаты (Vп-Vж, y1-x1). Таким образом, имеем до точки азеотропа: Vп-Vж > 0, y1-x1 > 0, Тогда частный объемный фазовый эффект жидкой фазы будет равен (рис 3.1):
Аналогичные построения на диаграмме делаем в области после точки азеотропа и получаем: Vп-Vж > 0, y1-x1 < 0, Имеем частный фазовый эффект жидкой фазы в случае бинарной азеотропной смеси с минимумом температуры кипения: В случае энтропии частные фазовые эффекты определяются аналогично. Для жидкой фазы частный энтропийный фазовый эффект: Частные энтропийные фазовые эффекты жидкой фазы показаны на рисунке 3.2. На рисунке 3.3 представлено изменение объема и концентрации в паровой фазе. В области до точки азеотропа имеем: Vж-Vп < 0, x1-y1 < 0, Получаем частный объемный фазовый эффект для паровой фазы После точки азеотропа Vж-Vп < 0, x1-y1 > 0, Частный объемный фазовый эффект паровой фазы для бинарной азеотропной смеси с минимумом температуры кипения: Аналогично для энтропии (рис. 3.4): Частные энтропийные фазовые эффекты паровой фазы показаны на рисунке 3.4. В случае азеотропа с максимумом температуры кипения (рисунок 3.5 – 3.8) частные фазовые эффекты в случае азеотропного состава соответственно равны и Для систем с максимумом температуры кипения изотермо-изобары имеют минимум объема (энтропии), то есть, обращены в обеих фазах выпуклостью вниз. Для определения фазовых эффектов в жидкой фазе используются конноды, проекции которых дают ноды, ориентированные от жидкости к пару. Снова будем рассматривать две области до и после точки азеотропа. В области до точки азеотропа (рис. 3.5): Vп-Vж > 0, y1-x1 < 0, В этом случае имеем частный объемный фазовый эффект после точки азеотропа Vп - Vж
> 0, y1-x1 > 0, Таким образом, получаем частный объемный фазовый эффект в случае бинарной азеотропной смеси с максимумом температуры кипения Аналогично в случае энтропии (рис. 3.7) Теперь рассмотрим систему относительно паровой фазы (рис 3.6). В области до точки азеотропа получаем: Vж-Vп < 0, x1-y1 > 0, В области после точки азеотропа Vж-Vп < 0, x1-y1 < 0, Аналогично в случае энтропии (рис. 3.8): 3.2. Фазовые эффекты и уравнение Ван-дер-Ваальса для гетероазеотропных смесей. На рисунках 3.10 – 3.13 редставлены диаграммы объем – состав фаз и энтропия – состав фаз гетероазеотропных бинарных смесей. В этих смесях в треугольнике расслоения наблюдается следующая закономерность При этом уравнения Ван-дер-Ваальса выглядят следующим образом
Из этих трех уравнений два независимы. При постоянном давлении имеем: или Аналогичные уравнения можно получить для паровой фазы. В этом случае при Р = const Следовательно, получаем 3.3. Уравнение Ван-дер-Ваальса в терминах общих и частных фазовых эффектов. Используя общие и частные фаэовые эффекты можно представить уравнение Ван-дер-Ваальса в форме: для жидкой фазы для паровой фазы В азеотропных точках
4. Заключение. 1. Определены частные фазовые эффекты для бинарных азеотропных смесей при постоянных давлении и температуре. 2. Определены общие и частные фазовые эффекты в азеотропной точке, а также слева и справа от азеотропного состава. 3. Представлено уравнение Ван-дер-Ваальса в терминах общих и частных фазовых эффектов. Список использованной литературы: 1. Сторонкин А.В. Термодинамика гетерогенных систем. Изд. ЛГУ. 1967г. ч.1и 2. 448с. 2. Серафимов Л.А., Фролкова А.К. Общие закономерности классификации бинарных жидких растворов в терминах избыточных термодинамических функций. АО Росвузнаука 1992г. 40с. 3. Серафимов Л.А., Фролкова А.К., Раева В.М. Термодинамический анализ пространства избыточных функций смешения бинарных растворов.//ТОХТ – 1996. Т. 30, №6. С.611-617. 4. Findley A. The phase rule and its applications, seventh edition. Longmans, green and Co, London, New York, Toronto 1931. Перевод Раковского А.В. ОНТИ 1935г. 5. Палатник Л.С., Ландау А.И.. Фазовые равновесия в многокомпонентных системах. Изд. Харьковского университета 1961г. 407с. 6. Биттрих Г.И., Гайле А.А., Лемпе Д., Проскуряков В.А., Семенов Л.В. Разделение углеводородов с использованием селективных растворителей. Химия 1987г. 192с. 7. Коган В.Б. Гетерогенные равновесия. Химия Л.:1968г. 432с. 8. Пригожин И.Р., Дефэй. Химическая термодинамика. Наука. Новосибирск. 1966 г. 510с. 9. Партингтон Д.Р., Раковский А.В. Курс химической термодинамики. Пер. с англ. Герасимова Я.И. Издание второе.1932г. Гос. науч. техн. изд-во. 384с. 10. Аносов В.Я., Озерова М.И., Фиалков Ю.Я. Основы физико-химического анализа. Наука 1976г. 504с. 11. Касаткин А.Г. Основные процессы и аппараты химической технологии. Химия 1971г., 784с. 12. Древинг В.П., Калашников П.А. Правило фаз с изложением основ термодинамики. Изд. МГУ 1964г. 456с. 13. Гиббс Д.В. Термодинамика, статистическая механика. Наука. М. 1982г. 584с. 14. Мюнстер А. Химическая термодинамика. Пер. с нем. под ред. Герасимова Я.Ч. Мир 1971. 296с. 15. Серафимов Л.А. Преобразование Лежандра и его роль в химической технологии. //Ученые записки МИТХТ 2001г., в. 3. С.4-12 16. Львов С.В. Рукопись лекций по технологии Основного органического синтеза. 1956г. 105с. 17. Гельперин Н.И. Дистилляция и ректификация. Госхимиздат. 1947 г. 312с. 18. Кириллин В.А., Шейндлин. Термодинамика растворов. Госэнергоиздат. 1980 г. 288 с. Обозначения.
|
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


 V S
V S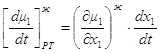 1.40
1.40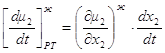 1.41
1.41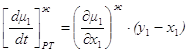 1.42
1.42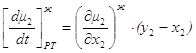 1.43
1.43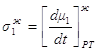 1.44
1.44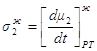 1.45
1.45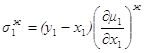 1.46
1.46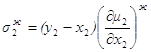 1.47
1.47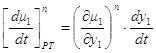 1.48
1.48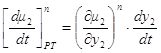 1.49
1.49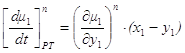 1.50
1.50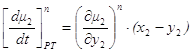 1.51
1.51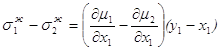
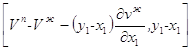
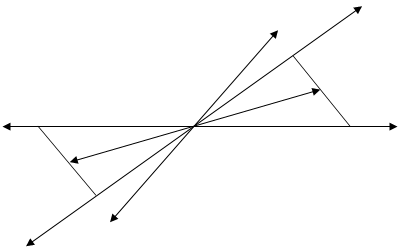 < S, x1, x2 > и <- S, -x1, - x2 > S
< S, x1, x2 > и <- S, -x1, - x2 > S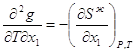 2.23
2.23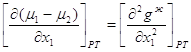 2.24
2.24 2.25
2.25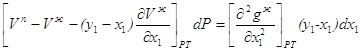 2.26
2.26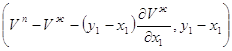 .
.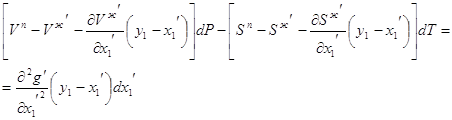 3.21
3.21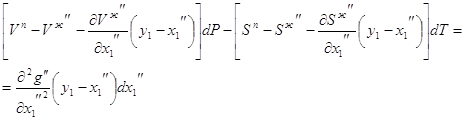 3.22
3.22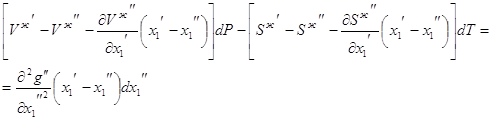 3.23
3.23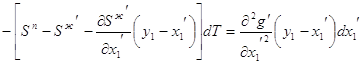 3.24
3.24 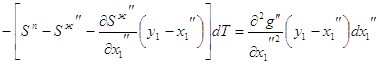 3.25
3.25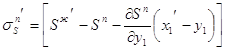 3.28
3.28 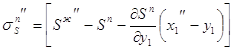 3.29
3.29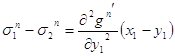 3.30
3.30 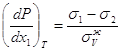 3.33
3.33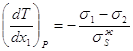 3.34
3.34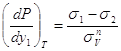 3.35
3.35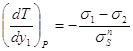 3.36
3.36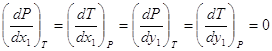 3.37
3.37