|
Лабораторная работа: Визначення кількості витків в обмотках трансформатораЛабораторная работа: Визначення кількості витків в обмотках трансформатораПерелік лабораторних робіт з фізики
Лабораторна робота №11 (2 години)Тема Визначення кількості витків в обмотках трансформатора1 Мета роботи: набути уміння обчислювати коефіцієнт трансформації та кількість витків в обмотках трансформатора. 2 Прилади і обладнання:
2.1 Розбірний трансформатор (дві котушки і залізне осердя) 2.2 Джерело змінного струму (КЕФ-8) 2.3 Один або два вольтметри на змінний струм 2.4 Дріт для виготовлення додаткової обмотки 2.5 Пуста котушка 2.6 З’єднувальн провідники 4-6 шт. 3 Загальні теоретичні положення Відомо, що електричну енергію зручно і просто передавати від генератора до споживача. Проте воно пов’язано із значними втратами в проводах, внаслідок їх нагрівання. Ефективним шляхом зменшення теплових втрат у проводах лінії передач є одночасне зменшення сили струму зі збільшенням напруги при незмінній потужності струму. Тому передавання електроенергії на далекі віддал стало можливим лише після того, як П. М. Яблочков винайшов трансформатор. Трансформатор це пристрій, призначений для перетворення змінного струму однієї напруги U1 у змінний струм іншої напруги U2, але тієї самої частоти.
Малюнок 1 – Схема трансформатора, що підвищу напругу (підвищувальний трансформатор) Трансформатор складається з двох котушок (обмоток), надітих на замкнене залізне осердя. Первинна обмотка вмикається до джерела змінно напруги, а до вторинної обмотки під’єднують користувача електроенергії. За допомогою залізного осердя змінне магнітне поле з першої котушки потрапляє у другу котушку, де збуджується електрорушійна сила (ЕРС) Е за законом електромагнітної індукції:
Оскільки магнітний потік в середині осердя однаковий у всіх
перерізах, то в кожному витку первинної і вторинної обмотках виникає однакова ЕРС
ндукції -
де n1 – кількість витків первинної обмотки, шт.; n2 – кількість витків вторинної обмотки, шт.; Е1, Е2 ЕРС у першій, другій обмотках, В.
Коефіцієнт k називають коефіцієнтом трансформац його визначають під час холостого ходу трансформатора, коли розімкнуто коло вторинної обмотки. Тому
де U1 – напруга на затискачах первинної обмотки, В; U2 – напруга на затискачах вторинної обмотки, В. Якщо U1 < U2, то трансформатор називається підвищувальним, а при U1 > U2 – знижувальним. Один і той самий трансформатор можна використовувати, як підвищувальний, так і знижувальний, якщо поміняти місцями його обмотки. Оскільки ККД трансформатора дуже близький до 1, то для спрощення розрахунків можна знехтувати втратами потужності в трансформаторі (нагрівання обмоток, розсіяння магнітного поля,... ) і вважати, що Р1 ≈ Р2:
де I1 , I2 – сила струму у первинній, вторинній обмотці відповідно, А. Звідки знайдемо:
З формули 4 видно, що при підвищенні напруги, сила струму зменшується і, навпаки, при зниженні напруги, сила струму збільшується. Тому. при зниженні напруги, у другій котушці тече більший струм потрібно використовувати провідник більшого діаметра, ніж у першій котушці. 4 Порядок виконання роботи4.1 Намотати на пусту котушку додаткову обмотку, підрахувавши при цьому кількість її витків n0. 4.2 Приєднати трансформатор до джерела змінної напруги так, щоб додаткова обмотка була вторинною. 4.3 Виміряти напругу U1 на первинній та U0 на вторинній обмотках і обчислити коефіцієнт трансформації:
4.4 За відомим коефіцієнтом трансформації:
обчислити кількість витків n1 первинно обмотки:
4.5 Для визначення кількості витків у вторинній обмотці n2 знову приєднують трансформатор до джерела струму зробивши другу котушку первинною і залишивши додаткову котушку у місті вторинної обмотки. 4.6 Виміряти напругу на обмотках U2 і U0 і обчислити коефіцієнт трансформації:
4.7 За відомим значенням коефіцієнта трансформації k2 обчислити кількість витків n2 вторинної обмотки:
5 Контрольн запитання5.1 Для чого призначений трансформатор і яка його будова? 5.2 Що називають коефіцієнтом трансформації? 5.3 Що відбудеться у другій обмотці трансформатора, якщо на першу обмотку подати постійну напругу? 5.4 Який тип трансформатора використовують для зварювального апарата, якщо для зварювання металів потрібен великий струм? 5.5 Чи можна зняти котушку трансформатора з осердя і подати на неї напругу, яка вказана на ній? 5.6
У скільки
разів треба підвищити напругу, щоб втрати зменшити у n раз? (Використати
формули 5.7 Чому ККД трансформатора значно вищій ніж ККД електродвигуна? 5.8 Який ще снує шлях зменшення теплових втрат у провіднику, крім зменшення сили струму? 5.9 Який тип трансформатора використовують біля електростанції, біля користувача? 6 Висновки7 Оформлення звітуЛабораторна робота №12 (2 години)Тема Визначення показника заломлення скла1 Мета роботи: навчитись визначати показник заломлення скла. 2 Прилади і обладнання:
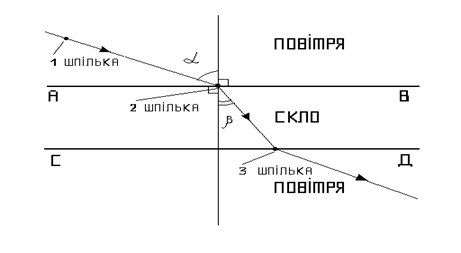
7.1 Скляна пластинка з паралельними гранями 7.2 Аркуш паперу 7.3 4 кнопки 7.4 Транспортир 7.5 3 шпильки 7.6 Олівець 7.7 Трикутник 7.8 Дощечка 7.9 8 Загальні теоретичні положення Кожний промінь світла, що проходе з одного середовища в інше, на межі цих середовищ заломлюється. Заломлення світла – це зміна напрямку розповсюдження світла при переході з одного середовища в друге. Причина заломлення світла – зміна його швидкості поширення. Кут між падаючим променем і перпендикуляром до поверхні, опущеним у точку падіння променя, називають кутом падіння (α). Кут між заломленим променем і продовженням перпендикуляра, опущеним у точку падіння променя, називають кутом заломлення (β).
Малюнок 1 - Схема досліду Закон заломлення світла. При всіх змінах кутів падіння α і заломлення β відношення синуса кута падіння до синуса кута заломлення для даних двох середовищ є величина стала, яка називається відносним показником заломлення n другого середовища відносно першого: де α – кут падіння променя; β – кут заломлення променя; n1 ,n2 – абсолютні показники заломлення 1 середовища і 2 середовища відносно вакууму (пустоти); n – (відносний) показник заломлення скла відносно повітря; Абсолютним показником заломлення nабс є величина, яка визначається відношенням швидкості світла у вакуумі с до швидкості світла υ у даному середовищі.
Тому для двох середовищ маємо:
де υ1 , υ2 – швидкості поширення світла у першому середовищі і у другому відповідно; с – швидкість світла у вакуумі; с=299729500 м/с ≈ 3*108 м/с. З формули 3 видно, що відносним показником заломлення n другого середовища відносно першого відношення швидкост поширення світла у другому середовищі до швидкості у першему. Таблиця Абсолютний показник заломлення деяких речовин
9 Порядок виконання роботи4.8 Поклавши скляну пластинку на пришпилений до дощечки аркуш паперу, прокреслити олівцем лінії вздовж заломлюючих граней АВ і СД (малюнок 1). 4.9 Встромити в дощечку дві шпильки так, щоб одна з них дотикалася до пластинки, а проведений через них відрізок прямої утворював би з гранню довільний кут. 4.10 Піднявши дощечку на рівень очей, встромити третю шпильку так, щоб вона (якщо дивитися через пластинку) закрила дві перші шпильки. 4.11 Знявши пластинку і витягнувши шпильки, сполучити місця проколів відрізками прямої лінії. 4.12 Виміряти транспортиром кути падіння α і заломлення β. 4.13 Обчислити відносний показник заломлення скла n за формулою 1: Таблиця 2 Дані вимірювань і обчислень
4.14 Повторити дослід для інших кутів падіння і порівняти результати. Визначити середнє значення показника заломлення:
4.15 Визначити абсолютну похибку для кожного випадку:
де і – номер досліду. 4.16
Обчислити:
4.17 Обчислити відносну похибку вимірювань:
4.18 результати записати у вигляді:
10 Контрольн запитання10.1 Як читаються перший та другий закони заломлення світла? 10.2 Що називають абсолютним, відносним заломленням світла? 10.3 Чи знаходяться падаючий заломлений промені у одній площині? 10.4 Як відомо, скло – прозорий матеріал; однак бите скло непрозоре та має білий колір. Чим це пояснюється? 10.5 Чи буде вихідний промінь паралельний падаючому, якщо перед пластинкою і за пластинкою є різн середовища? 10.6 Де більше швидкість поширення світла: у повітрі чи у дослідному склі? У скільки разів? (таблиця 1) 10.7 Коли відносний показник заломлення світла другого середовища відносно першого буде більше 1, менше 1? 10.8 Визначити граничний кут при переході променів з алмазу в кристалічний цукор (таблиця 1). 11 Висновки12 Оформлення звітуЛабораторна робота №13 (2 години)Тема Спостереження явища інтерференції світла1 Мета роботи: спостерігати явище інтерференції світла. 2 Прилади і обладнання:
12.1 Дв скляні пластинки 12.2 Дротяна рамка на підставці 12.3 Мильна вода 12.4 Збиральна лінза 12.5 Екран 13 Загальні теоретичні положення
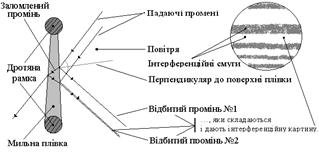
Інтерференція світлових хвиль – додавання двох хвиль, внаслідок якого спостерігається стійка з часом картина підсилення або послаблення результуючих світлових коливань у різних точках простору. Для спостереження інтерференції хвилі повинні бути когерентними (согласованими), тобто, вони повинні мати однакову частоту (ω1 = ω2) і сталу різницю фаз (∆φ = φ2 - φ1 = const). Отримати дві когерентні світлові хвилі від двох джерел практично неможливо, тому що велика кількість збуджених атомів джерел світла одночасно, самовільно (спонтанно) і хаотично за часом та за напрямком випромінюють це світло, яке, у наслідок цього, не є когерентним. Але, за допомогою приладів, якщо взяти одне звичайне джерело світла, розділити пучок світла на два пучка, змусити їх піти різними шляхами з різними довжинами, а потім звести їх у одне й те саме місто, то при їх накладанні, виникне інтерференційна картина (чергування світлих і темних смуг - максимумів і мінімумів коливань). Темні смужки відповідають послабленню коливань (інтерференційні мінімуми), а світлі смужки – їх посиленню (інтерференційні максимуми). Розділити світловий промінь можна за допомогою двох щілин, звичайних і напівпрозорих дзеркал, плівки, біпризми (досліди з дзеркалами, біпризмами Френеля; лупою зі скляною пластинкою для спостереження кілець Ньютона ). Певне значення частоти (ω, ν) характеризу колір світлової монохроматичної хвилі і у інтерференційній картині світл смужки будуть того ж кольору, тому що при накладуванні хвиль їх частота не змінюється (ω, ν =const), а змінюється лише результуюча амплітуда коливань. Щоб надати можливість світловим пучкам пройти різні шляхи з різними довжинами, для отримання різниці фаз (∆φ), використовують тонкі прозорі плівки змінної товщини. Світловий промінь одразу ж частково відбивається від зовнішньої поверхні плівки (утворюється 1 пучок), нша частина пучка, після заломлення, відбивається від внутрішній поверхн плівки (утворюється 2 пучок), які обидва потім йдуть у одному напрямку і за межами плівки накладаються один на одне, утворюючи інтерференційну картину. Але деяка частина світлового пучка повністю проходе скрізь плівку. Дивиться малюнок 1.
Малюнок 1. Схема досліду інтерференції у мильній плівц змінної товщини і зображення інтерференційної картини При використанні у дослідах двох скляних пластинок маємо між ними повітряний шар змінної товщини, а при використанні дротяної рамки - мильну водяну плівку з клиноподібною формою, стовщеної донизу за рахунок сили тяжіння. Якщо, при накладуванні хвиль відбувається посилення коливань, то різниця ходу хвиль дорівнює цілому числу довжин хвиль:
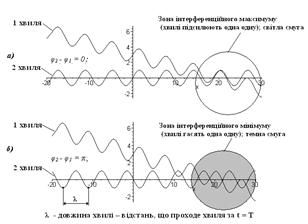
де ∆d – різниця ходу, м; λ – довжина хвилі, м; k = 0, 1, 2, ... - порядковий номер максимуму інтерференції . Дивиться малюнок 2а. Якщо, при накладуванні хвиль відбувається послаблення коливань, то різниця ходу хвиль дорівнює непарному числу половини довжини хвилі:
де k = 0,1,2,... – порядковий номер мінімуму інтерференції. Дивиться малюнок 2б.
Малюнок 2. Посилення (а) і послаблення (б) двох хвиль при їх складуванні 14 Порядок виконання роботи4.1 Старанно потерши скляні пластинки, скласти їх разом стиснути пальцями. 4.19 Розглянути пластинки у відбитому світлі на темному фоні. При цьому пластинки слід розміщувати так, щоб на поверхні скла не виникали яскраві полиски (бліки) від вікон чи білих стін. 4.20 Зверніть увагу, що в окремих місцях дотику пластинок виникає інтерференційна картина у вигляді яскравих кільцеподібних або неправильної форми смуг. Змінивши стискання пластин, розглянути зміну форми й розміщення інтерференційних смуг. 4.21 Опустивши дротяну рамку в мильну воду, а потім витягнувши її, домогтися утворення мильної плівки. 4.22 Спрямувавши на плівку за допомогою лінзи біле світло, спостерігати виникнення на екрані інтерференційно картини у відбитому світлі у вигляді кольорових горизонтальних смуг (Малюнок 1). 15 Контрольн запитання15.1 Які світлові хвилі називають когерентними? 15.2 Назвіть необхідні умови спостереження інтерференції світла. 15.3 Яким шляхом можна здобути когерентні хвилі від звичайного джерела спонтанного випромінювання світла? 15.4 Навіщо дві склян пластинки складають разом, а після їх стискають пальцями? 15.5 Як вигляда нтерференційна картина при освітленні плівки монохроматичним, білим світлом? 15.6 Чому відповідають на екран темні і світлі смуги при спостереженні інтерференції? 15.7 Що буде на екрані від хвиль довжиною λ = 500 нм, якщо різниця ходу (∆d) така: 2000 нм, 1250 нм? 15.8 Поясніть, чому біле світло після відбивання від плівки дає , на екрані багатокольорову інтерференційну картину? 15.9 Чим пояснити виникнення кольорових смуг у тонкому шарі керосину, плаваючого на поверхні води? 15.10 Які властивості світла підтверджує явище інтерференції світла? 15.11 Поясніть навіщо і як просвітляють оптику (лінзи фотокамер), як досліджують якість відполіровано поверхні, використовуя явище інтерференції. 16 Висновки17 Оформлення звітуЛабораторна робота №14 (2 години)Тема Вимірювання довжини світлової хвилі за допомогою дифракційної решітки1 Мета роботи: дослідним шляхом виміряти довжину світлової хвилі. 2 Прилади і обладнання:
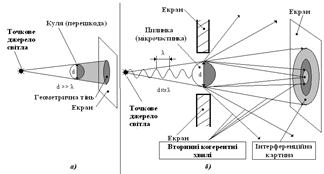
17.1 Електрична лампа з прямою ниткою розжарення (одна на весь клас) 17.2 Прилад для визначення довжини світлової хвилі. 18 Загальні теоретичні положення При відсутності перешкод у однорідному просторі світло розповсюджується прямолінійно. Якщо є перешкоди, то за законами геометричної оптики за ними з’являються тіні, в яких світло не може з’явитись ( Малюнок 1а ). Оскільки світло можна розглядати як хвилю, а не тільки як потік частинок (фотонів), то за законами хвильової теорії світло може з’являтись в області геометричної тіні або з’являтись і розповсюджуватись у напрямках, не співпадаючих з початковим напрямком світлового променя. Прикладом цього є існування світлої плями у самому центрі тіні від непрозорої кулі, що освітлюють з одного боку (дослід Френеля). ( Малюнок 1б ). Коли на шляху світлової хвилі є перешкода (мікрочастинка, тонкий дріт, вузька щілина), лінійні розміри якої порівняні з довжиною λ хвилі, то після взаємодії з цією перешкодою світлова хвиля змінює свій напрямок розповсюдження. Явище огинання хвилями країв перешкод і відхилення хвиль від прямолінійного поширення називається дифракцією хвилі. Дифракцію можна спостерігати коли розміри перешкод d порівнян з довжиною λ хвилі (d ≈ λ). Існування явища дифракції можна пояснити за допомогою принципу Гюйгенса, а саме: у місці взаємодії світлової хвилі з перешкодою існують фіктивні когерентні світлові джерела, які по всім можливим напрямкам випромінюють когерентні світлові хвилі. Останні, об’єднуючись одна з одною, утворюють явище інтерференції, яка виглядає на екрані як сукупність світлих і темних смуг.
Малюнок 1. Взаємодія світлових хвиль з великими (а) малими об’єктами (б) Оскільки довжина світлової хвилі дуже мала λ ≈ 0,4 - 0,77 мкм, достатня ширина перешкод (прозорих щілин, непрозорих мікрочастинок) має бути порядку 1 мм. Щоб дістати яскравішу інтерференційну картину на екрані, слід пропускати світло не через одну щілину, а крізь кілька паралельних вузьких щілин. Для цього скористуємося дифракційною граткою, яка сукупністю багатьох дуже вузьких щілин, розділених непрозорими проміжками. ратки виготовляють у вигляді пластинок з прозорої твердої речовини, на поверхні яких алмазним різцем наносяться штрихи, паралельні один одному. Примітивними дифракційними гратками також є пташине перо, вії, кілька тонких паралельних дротів розташованих один біля одного. Назвемо щілину і розташовану біля неї непрозору частину елементом гратки. Тоді ширину d одного елемента назвемо періодом ґратки.
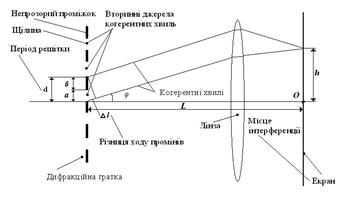
де d – період решітки, м; а – ширина щілини, м; b ширина непрозорої частини для світлої ділянки між двома щілинами, м. У цьому випадку відбувається інтерференція вторинних когерентних променів, які у різних напрямках йдуть від усіх щілин, в яких знаходяться фіктивні вторинні джерела когерентних хвиль. Лінза, що зображена на малюнку 2, збира паралельні когерентні хвилі в одну точку, положення якої на екрані задається відстанню h, що залежить від кута φ. Роль лінзи у досліді виконує око людини, яке баче інтерференційну картину.
Малюнок 2.- Принципова схема дослідно установки для визначення довжини світлової хвилі Різниця ходу вторинних хвиль залежить від кута φ . Умова спостереження дифракційного максимуму матиме такий вигляд:
де φ – кут між напрямками розповсюдження первинних та вторинних променів; k = 0, 1, 2, …. – порядок максимуму; λ – довжина хвилі, м. Умова спостереження дифракційного мінімуму матиме слідуючий вигляд:
За допомогою дифракційних ґраток дуже точно досліджують спектральний склад світла, тобто визначають частоти (ωі, νі) (або довжини хвиль λі) кожної і компоненти світла. 19 Порядок виконання роботи19.1 Вставити в рамку приладу дифракційну решітку. 19.2 Відсунути шкалу з вузькою прицільною щілиною на максимально можливу відстань від дифракційної решітки. 19.3 Спрямувати вісь приладу на лампу так, щоб через вузьку прицільну щілину щитка було видно нитку лампи. 19.4 Спостерігати по обидва боки від щілини на чорному фоні над шкалою дифракційні спектри. 19.5 Якщо спектри трохи нахилені відносно шкали, то це означає, що щілини дифракційної решітки не вертикальні. Треба усунути перекіс, повернувши рамку з решіткою на певний кут. 19.6 Не рухаючи приладу, за шкалою визначити положення середин кольорових смуг у спектрах першого порядку ( k =1 ). Результати записати в таблицю. Таблиця 1 Результати досліджень
19.7 Для першого порядку максимуму ( k =1 ) з формули 2 довжину хвилі можна визначити як
Оскільки k =1 , h << L , то при малих кутах (φ)
де h – відстань максимуму від точки О, м; L – відстань від решітки до екрану, м ( Малюнок 2). 20 Контрольн запитання20.1 Яке явище називають дифракцією світла, умови його спостереження? 20.2 Чому дифракційна гратка да нтерференційну картину? 20.3 Є дві дифракційні гратки: в першої у 1 мм знаходиться 50 щілин, а в другій - у 1 мм знаходиться 100 щілин. Яка гратка має більшу дозволяючу можливість? 20.4 Визначити період гратки, якщо на 1 мм нанесено 20 щілин, 40 щілин, 50 щілин. 21 Висновки22 Оформлення звітуЛабораторна робота №15 (2 години)Тема Визначення оптичної сили та фокусної відстан збиральної лінзи1 Мета роботи: визначити фокусну відстань збиральної лінзи та її оптичну силу. 2 Прилади і обладнання:
22.1 Збиральна лінза 22.2 Напрямляюча рейка 22.3 Лампочка на підставці 22.4 Джерело струму 22.5 Вмикач 22.6 З’єднувальн провідники 22.7 Екран 23 Загальні теоретичні положення Для отримання зображень різного виду в оптичних приладах дуже часто використовують лінзи, дзеркала, призми. Такими оптичними приладами є: проекційний апарат для збільшення зображення малюнків, фотознімків, креслень; фотографічний апарат для отримання фотознімків тих об'єктів, що знаходяться перед ним; мікроскоп, що дозволяє велике збільшення зображення при розгляданні малих предметів; телескоп для наглядання за космічними тілами; бінокль – універсальний компактний прилад для спостереження за віддаленими наземними об’єктами. Лінза – це прозоре тіло з показником заломлення, відмінним від показника заломлення навколишнього середовища, обмежено двома правильними геометричними поверхнями (сферичними або комбінацією сферичною та плоскої).
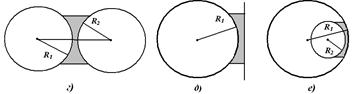
Малюнок 1.- Зображення лінз: а) опуклої; б) прямої з одного боку ї опуклої з іншого; в) вгнуто – опуклої; г) вгнутої; д) вгнутої з одного боку ї прямої з іншого; е) вгнуто – опуклої Лінзи бувають опуклими (паралельні промені після заломлення в ній сходяться за її межами) та вгнутими (паралельні промені після заломлення в ній розходяться за її межами). Тобто, опуклі лінзи є збираючи, а вгнут розсіюючи.
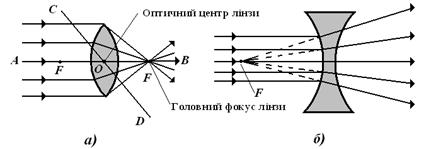
Малюнок 2. Збираюча (а) і розсіююча (б) лінзи. Головна оптична вісь – пряма (АВ), яка з’єднує центри сферичних поверхонь. (Малюнок 2а) Оптичний центр лінзи – точка (О) на головній оптичній осі всередині лінзи, при проходженні через яку проміні не заломлюються, тобто, не змінють напрямок розповсюдження. (Малюнок 2а) Побічна оптична вісь – будь-яка пряма (СD), яка проходить через оптичний центр лінзи. (Малюнок 2а) Головний фокус лінзи – точка (F) на головній оптичній осі, в якій після проходження лінзи збираються промені, що падають на неї паралельно головній оптичній осі (АВ). (Малюнок 2а) Фокальна площина – площина, проведена через головний фокус лінзи (F) перпендикулярно головній оптичній осі (АВ). Головна фокусна відстань F - відстань (OF) між оптичним центром лінзи (точка О) та її головним фокусом (F). (Малюнок 2а) Оптична сила лінзи - величина, що обернена до фокусно відстані лінзи:
де F – фокусна відстань лінзи, м; D – оптична сила лінзи, 1/м = 1 м-1 = 1 дптр (діоптрія), (1 діоптрія - це оптична сила лінзи з F =1 м).
Також оптична сила визначається за формулою 2:
де n – показник заломлення скла, з якого виготовлена лінза; R1, R2 – радіуси кривизни сферичних поверхонь лінзи. (Малюнок 1) Лінза називається тонкою, якщо її товщина (h) мало порівняно з радіусами кривизни поверхонь (R1, R2), що обмежують її. Тобто, h << R1 і h << R2. Для тонкої лінзи справедливе співвідношення:
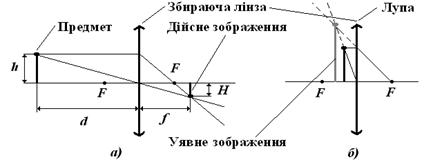
де d відстань від предмета до лінзи, м; f – відстань від лінзи до зображення; F – фокусна відстань. Лінійним збільшенням лінзи (Г) називається відношення розмірів зображення (Н) до розмірів предмета (h):
Зображення, що виходить при перетинанні променів, заломлених лінзою, за їх ходом, називають дійсним, а проти їх ходу – уявним. При побудові зображень використовують промені, хід яких відомий для будь-якої лінзи: промінь, який проходить через центр лінзи під будь-яким кутом, зберігає свій напрямок; промінь, паралельний головній оптичній осі в збираючій лінзі, проходить через фокус, а в розсіюючій лінзі його напрямок буде таким, що виходить з фокусу; промінь, що проходить через фокус у збираючій лінзі і ма напрямок на фокус у розсіюючій лінзі, після заломлення йдуть паралельно головній оптичній осі. Якщо на головній оптичній осі встановити початок відліку у оптичному центрі відліку (точці О) , то для збираючій лінзи можна дослідити залежність параметрів зображення від величини відстані d між лінзою і предметом. Для Для Для Аналогічним методом можна визначити залежність параметрів зображення від положення предмета для розсіюючій лінзи. 24 Порядок виконання роботи4.23 Поставити джерело світла на край стола, а екран у другого краю. Між ними поставити лінзу. Посовувати лінзу вздовж лінійки до тих пір, поки на екрані не буде різке зображення предмета. 4.24 Виміряти відстань від предмета до лінзи d та відстань від лінзи до екрана f , звернув увагу на необхідність їх точно вимірювати. 4.25 При сталому положенн джерела світла і лінзи (d=const) повторити дослід декілька разів, кожного разу знову отримуя різке зображення на екрані, рухаючи екран. 4.26 Обчислити Таблиця 1Результати вимірювань
4.27 Абсолютну похибку ∆D вимірювань оптичної сили лінзи можна обчислити за формулою 5:
де ∆d і ∆f – абсолютні похибки в вимірюваннях. При визначенні ∆d і ∆f слід мати на увазі, що вимірювання відстаней d і f не може бути виконано з похибкою, менше половини товщини лінзи. Так як досліди проводяться при сталому d, то:
Похибка вимірювань f буде більше на
4.28 Виміряти товщину лінзи h, та обчислити ∆D за формулою 8:
4.29 Записати результати у вигляді:
25 Контрольн запитання25.1 Що називають лінзою? 25.2 Які види лінз ви знаєте? 25.3 Як називають ту точку, у якій збираються паралельні промені після їх заломлення? Яка геометрична фігура визначає її місце положення? 25.4 Назвіть оптичні прилади, як ви знаєте. 25.5 Яке призначення у лінзи? Яким чином можна здобути вогонь, користуючись нею? 25.6 Для лінзи з R1 = R2 = F, користуючись експериментальними даними обчисліть відносний показник заломлення скла за формулою 2. 25.7 Побудувати у реальному масштабі зображення вертикального предмету висотою 2 см, що знаходиться на відстані d = 6 см від лінзи з фокусною відстанню F = 3см. Виміряти відстань від лінзи до накресленого зображення та порівняти його зі значенням, що обчислено за допомогою формули 4 (f=...). Для будови зображення предмету користуйтеся малюнком 3. 25.8 Відстань між предметом і його зображенням 72 см. Збільшення лінзи дорівнює 3. Знайти фокусну відстань лінзи. 25.9 З висоти 1 км сфотографовано річку. Визначити ширину річки, якщо на знімку вона дорівнює 4 см. Оптична сила об’єктива фотоапарата дорівнює 8 дптр.
Малюнок 3. Предмет і його дійсне перевернуте зображення (а), предмет і його уявне не перевернуте зображення (б). 26 Висновки27 Оформлення звіту |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |



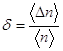
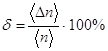 (5)
(5)

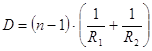 ,
(2)
,
(2)