|
Учебное пособие: Дифференциальное уравнение теплопроводимостиУчебное пособие: Дифференциальное уравнение теплопроводимостиДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ Общие вопросы теории теплообмена Неравномерное распределение температуры в металле, характерное для сварки и других видов местной тепловой обработки металла, неустойчиво. С течением времени температура в неравномерно нагретом теле выравнивается, причем более нагретые части отдают тепло непосредственно соприкасающимся с ними менее нагретым частям. Такой энергетический обмен между взаимодействующими телами или их отдельными частями с неодинаковой температурой называется теплообменом или теплопередачей. Количество энергии, переданной частицами более горячего тела частицам более холодного, называется количеством теплоты, или просто теплотой. При этом теплота переходит от точек с более высокой температурой к точкам с более низкой температурой, если процесс протекает в одном теле. При теплообмене между различными телами это положение также сохраняется, т. е. теплота переходит от более нагретых к более холодным телам. Таким образом, конечный результат теплообмена между ограниченными телами или частями одного и того же тела заключается в уравнивании их температур, после чего процесс прекращается. Понятие «теплообмен» охватывает совокупность всех явлений, при которых имеет место перенос некоторого количества теплоты из одной части пространства в другую в твердых, жидких и газообразных телах. Эти процессы по своей физико-механической природе весьма многообразны, отличаются большой сложностью и обычно развиваются в виде целого комплекса разнородных явлений. Для удобства принято делить перенос теплоты на простейшие виды: теплопроводность, конвекцию, теплообмен излучением, или радиацией. Эти процессы глубоко различны по своей природе и характеризуются различными законами. Соответственно этому и строится математическая теория описания каждой формы теплообмена, со своими уравнениями, своими математическими методами, аналитическими или численными, или методами аналогий. Теплопроводность характеризуется тем, что ее действие связано с наличием вещественной среды и что теплообмен может происходить только между такими частицами тела (молекулами и атомами), которые находятся в непосредственной близости друг от друга. Явление это можно представить себе так, что теплота переходит от одной частицы к другой, однако при этом сами частицы не перемещаются. В чистом виде процесс теплопроводности наблюдается в твердых телах. Конвекция наблюдается тогда, когда материальные частицы какого-нибудь тела изменяют свое положение в пространстве и при этом переносят содержащуюся в них теплоту. Это явление имеет место в жидкостях и газах и всегда сопровождается теплопроводностью, т. е. передачей теплоты от одной частицы к соседней, если только во всей текущей массе нет полного равенства температур. Теплообмен между средой и стенкой называют теплоотдачей. Теплообмен излучением характеризуется отсутствием контакта между телами, обменивающимися теплотой. Примером может служить излучение Солнцем теплоты на Землю через космическое пространство, в котором, как известно, плотность вещества ничтожна. Явление теплового излучения возникает у поверхности или внутри тела в результате сложных молекулярных и атомных возмущений. При этом некоторая часть внутренней энергии тела преобразуется в электромагнитные волны (или в другом представлении в фотоны — кванты энергии) и уже в такой форме передается через пространство. Все эти различные формы переноса теплоты не обособлены и в чистом виде встречаются лишь на отдельных участках пути прохождения теплоты. В большинстве случаев один вид теплообмена сопутствует другому и разделить их между собой очень трудно. Одним из законов, лежащих в основе аналитической теории теплопроводности, является гипотеза Фурье, связывающая перенос теплоты внутри тела с температурным состоянием в непосредственной близости от рассматриваемого места. Поэтому при изучении теории теплопроводности прежде всего необходимо установить основные понятия, такие, как температурное поле, градиент температуры, вектор теплового потока. Температурное поле Температурным полем называется совокупность значений температуры во всех точках рассматриваемого пространства (тела) в каждый фиксированный момент времени. Температура является скалярной величиной, так как она характеризует тепловое состояние в любой точке тела, определяя степень его нагретости. Температуре нельзя приписать какое-либо направление и поэтому температурное поле является скалярным. Математическим выражением распределения температуры в теле является выражение, содержащее в качестве независимых переменных пространственные координаты и время: в декартовой системе координат Т=Т(х,у,z,t); (2.1) Основной задачей аналитической теории теплопроводности является изучение пространственно-временного изменения температуры, т. е. нахождение зависимости (2.1). Уравнение (2.1) является записью наиболее общего вида температурного поля, когда температура в теле изменяется с течением времени и от одной точки к другой. Такое поле соответствует неустановившемуся тепловому режиму теплопроводности и называется нестационарным температурным полем. Если тепловой режим является установившимся, то температура в каждой точке тела с течением времени остается неизменной, меняясь лишь от точки к точке. Такое температурное поле называется стационарным и температура является функцией только координат, например в декартовых координатах Т=Т(х, у, z), ∂T/∂t=0. (2.2) Температурное поле, соответствующее уравнению (2.2), является пространственным, или трехмерным, так как температура является функцией трех координат. Если вдоль одной из координат температура остается постоянной, то математически это условие записывается (например, для координаты z) следующим образом: дТ/дz=0. В этом случае поле называется двумерным и записывается: для нестационарного режима Т=Т(х, у, t); для стационарного режима Т=Т(х, у). Если температура остается постоянной вдоль двух координат (например, у и z), то дТ/ду = дТ/дz = 0 и поле называется одномерным. В этом случае можно записать: для нестационарного режима Т=Т(х, t); для стационарного Т=Т(х). Переменные х, у, z, фигурирующие в уравнении (2.1), определяют положение любой точки рассматриваемого тела, являясь координатами этой точки в выбранной системе координат. Эти переменные могут принимать бесконечное множество числовых значений, как и переменная t, характеризующая время течения процесса теплопроводности. Совокупность всевозможных числовых значений переменных х, у, z, t, каждому из которых соответствует вполне определенное значение температуры Т=Т(х, у, z, t), называется областью определения функции Т(х, у, z, t). Функция Т(х, у, z, t) в своей области определения считается обычно непрерывной, дважды непрерывно дифференцируемой по пространственным координатам (х, у, z) и непрерывно дифференцируемой по времени t. В теле, имеющем температуру Т(х, у, z, t), можно выделить поверхность, во всех точках которой в некоторый момент времени температура одинакова. Такая поверхность называется изотермической поверхностью или поверхностью уровня. Уравнение поверхности уровня имеет следующий вид: Т(х, у, z, t)=C или Т=С, где C=const. В отличие от стационарных в нестационарных полях форма и расположение изотермических поверхностей с течением времени изменяются. Изотермические поверхности характеризуются следующими основными свойствами: а) две
изотермические поверхности, имеющие различные температуры, никогда не
пересекаются друг с другом, так как в одной и той же б) изотермические
поверхности не имеют границ внутри тела. Они в) теплота не
распространяется вдоль изотермической поверхности,
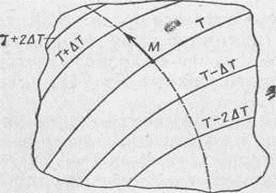
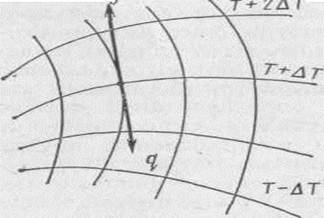
Рис. 2.1 Таким образом, можно считать, что изотермические поверхности разделяют твердое тело на тонкие «слои» изотермические оболочки, отделяющие часть тела с температурой, большей, чем T=С, от части тела с температурой, меньшей, чем Т=С. Пересечение изотермических поверхностей плоскостью дает на этой плоскости семейство изотерм (линии, соответствующие одинаковой температуре). Они обладают теми же свойствами, что и изотермические поверхности, т. е. не пересекаются, не обрываются внутри тела, оканчиваются на поверхности либо целиком располагаются внутри самого тела. На рис. 2.1 представлен участок двумерного температурного поля с изотермами Т, Т±∆Т, Т±2∆Т и т. д. Задание температурного поля соотношением Т=Т(х, у, z, t) не всегда дает достаточно ясное представление о поведении этого поля, а задание изотермических поверхностей (поверхностей уровня) с отметкой на них соответствующих значений температуры Т=С равносильно заданию самого поля Т=Т(х, у, z, t), при этом взаимное расположение поверхностей уровня даст наглядное представление о соответствующем поле температур. Указанный способ изображения поля особенно удобен, когда речь идет о двумерном поле. Равенство вида Т(х, у, t) = C (всюду время t фиксировано) определяет на плоскости (х, у) некоторую кривую у = φ(х, с, t). Такие кривые называются линиями уровня (изотермами) плоского (двумерного) температурного поля Т=Т(х, у, t) (рис. 2.2).
Рис. 2.2 На практике приходится иметь дело с температурными полями, обладающими специальными свойствами симметрии, облегчающими изучение таких полей. § 2.3 Температурный градиент
Рассмотрим две бесконечно
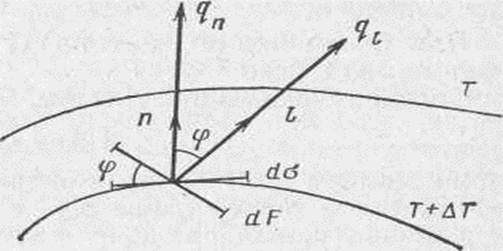
близкие изотермические поверхности Рис. 2.3 Перемещаясь из точки М вдоль любых направлений, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. Если перемещаться вдоль какого либо направления l, пересекающего изотермические поверхности, то наблюдается изменение температуры. Используя понятие производной скалярного поля по заданному направлению, можно описать его локальные свойства, т. е. изменение температуры Т при переходе от точки М к близкой точке М' по направлению l. Скорость изменения температуры Т в точке М в направлении l характеризуется производной функции Т дТ/дl= lim[T(M’) - Т(М)]/∆l. (2.3) ∆l→0 Наибольшая разность температуры на единицу длины вектора перемещения [Т(М")—Т(М)]/∆l наблюдается в направлении нормали n к изотермической поверхности (рис. 2.3). В соответствии с (2.3) максимальная скорость изменения температуры при этом равна пределу отношения изменения температуры ∆T к расстоянию между изотермическими поверхностями по нормали ∆n, когда ∆n стремится к нулю: дТ/дп= lim [T(M")—T(M)]/∆n= lim ∆T/∆n. (2.4) ∆n →0 ∆n →0 Итак, в любой точке М изотермической поверхности можно построить некоторый вектор, направленный по нормали к этой поверхности в сторону увеличения температуры. Абсолютная величина этого вектора равна изменению температуры на единицу длины перемещения в рассматриваемом направлении — скорости возрастания температуры в этом направлении (т. е. производной от температурной функции Т по направлению нормали n). Такой вектор называют градиентом температуры в точке М или градиентом температурного поля и записывают в виде символа grad T: в декартовых координатах (х, у, z) grad T = ∂T/∂x i + ∂T/∂y j + ∂T/∂z k (2.5) Для обозначения вектора (2.5) в теории поля иногда применяют символ gradT = T Согласно сказанному выше, можно записать |grad T| = ∂T/∂n (2.6) длина вектора grad Т равна скорости возрастания Т в этом направлении. Здесь и всюду далее n единичный вектор нормали. Температурный градиент показывает, насколько интенсивно (резко) меняется температура внутри тела. Производная от функции Т по направлению нормали n и вектор gradT связаны соотношением дТ/дп = п grad Т. (2.7) Вектор нормали n к поверхности T=const в точке М может иметь два противоположных направления, одно из которых можно считать внешним по отношению к данной поверхности, а другое внутренним. Если нормаль n направить в сторону больших температур, то дТ/дп>0 и, как следует из (2.7), градиент температуры будет направлен в ту же сторону (угол между векторами n и grad T равен нулю). Если нормаль направить в сторону убывающей температуры, то производные дТ/дп < 0 и gradT окажутся направленными противоположно этому направлению, т. е. опять в сторону возрастающей температуры. Тепловой поток. Векторная и скалярная формы закона Фурье В теле, не находящемся в полном тепловом равновесии (т. е. обладающим неравномерным распределением температуры), всегда происходит перенос теплоты. Отсюда следует, что для передачи теплоты теплопроводностью необходимо неравенство нулю температурного градиента в различных точках тела. Тепловой поток в отличие от температуры — величины скалярной имеет вполне определенное направление, а именно: от точек тела с более высокой к точкам с более низкой температурой. Таким образом, тепловой поток можно рассматривать как ректор, направленный в сторону уменьшения температур, а поле тепловых потоков — векторным. Для математического описания поля тепловых потоков вводится вектор q, называемый вектором плотности теплового потока. Под вектором плотности теплового потока в точке М температурного поля понимают вектор, направление которого совпадает с направлением переноса теплоты, а абсолютная величина выражает тепловой поток или интенсивность переноса теплоты, измеряемую количеством теплоты, проходящей в единицу времени через единицу площади поверхности, перпендикулярной направлению потока в рассматриваемой точке. Обозначим через dQ количество теплоты, проходящее через изотермическую поверхность площади dσ за время dt. Тогда, по определению, абсолютное значение вектора плотности теплового потока можно записать в виде q = dQ/ (dσ dt) (2.8) Формула (2.8) характеризует плотность теплового потока единичного элемента изотермической поверхности. Понятие плотности теплового потока, как будет показано ниже, применимо к любой, а не только к изотермической поверхности. Опыт показывает, что передача теплоты теплопроводностью происходит по нормали к изотермической поверхности от мест с большей температурой к местам с меньшей температурой. Следовательно, вектор плотности теплового потока направлен по нормали к изотермической поверхности в направлении падения температуры. Можно говорить о плотности теплового потока и вдоль любого другого направления l, отличного от направления нормали п. В этом случае плотность теплового потока в направлении l есть проекция вектора q на это направление, т.е. величина q·cos(n,l). Сущность гипотезы Фурье состоит в том, что тепловой поток через элемент изотермической поверхности вполне определяется значением температурного градиента в рассматриваемой точке М. Возникновение тепловых потоков вдоль изотермических поверхностей невозможно, так как по всей изотермической поверхности составляющая градиента температуры равна нулю. Следовательно, векторы плотности теплового потока q и grad T направлены по нормали к изотермической поверхности, но в противоположные стороны (рис. 2.4).
Рис. 2.4 С увеличением перепада температур, т. е. с возрастанием температурного градиента, увеличивается и плотность теплового потока. Опыты показали, что плотность теплового потока можно считать пропорциональной первой степени удельного перепада температуры. Это и явилось основой гипотезы Фурье о наличии простейшей количественной зависимости между абсолютными значениями векторов плотности теплового потока и температурного градиента. На основе этих данных, а также соображений о противоположном направлении этих векторов закон Фурье в векторном виде записывается следующим образом: q = - λ grad T. (2.9) Этот закон, сформулированный в виде гипотезы, был подтвержден многочисленными опытами. Выражение (2.9) описывает механизм теплопроводности и используется при выводе уравнения теплопроводности, лежащего в основе всех теоретических исследований процессов теплопроводности. Коэффициент пропорциональности λ называется теплопроводностью и является физической константой, характеризующей теплопроводящие свойства материала данного тела. Подставляя в уравнение (2.9) единицы q и температурного градиента, найдем для λ единицу Вт/(м-град). Числовое значение теплопроводности определяет количество теплоты, проходящее через единицу площади изотермической поверхности в единицу времени при градиенте температуры, равном единице. Значение теплопроводности в общем случае зависит от природы вещества, его структуры, влажности, давления, температуры и других факторов. В большинстве случаев теплопроводность λ для различных материалов определяется опытным путем, а при технических расчетах значение λ берется из справочных таблиц. С повышением температуры λ возрастает (что связано с увеличением скорости движения молекул и их учащенным соударением), от давления же λ практически не зависит. Выражение (2.8) запишем в виде dQ= q·dσ·dt. (2.10) Как отмечалось, нормаль п к элементу dσ изотермической поверхности может иметь два направления (направляющие косинусы этих направлений отличаются только знаками). Условимся считать тепловой поток положительным, если направление потока совпадает с выбранным направлением нормали, и отрицательным, если оно ему противоположно. Для абсолютных значений векторов, входящих в равенство (2.9), следует, что q=λ|gradT|. Теперь в равенстве (2.6) необходимо поставить знак минус, т. е. |grad Т|= - дТ/дп и q=—λ∂T/∂n. (2.11) Можно писать закон Фурье в скалярной форме: dQ=- λ(dT/dn)dσdt. (2.12) Выражение (2.12) определяет количество теплоты, проходящее через малый участок dσ изотермической поверхности за время dt по направлению нормали n к площадке dσ. Теплосодержание S [ватт/г] это количество теплоты, сообщённое твердому телу при нагреве до температуры T, отнесенное к единице его массы, отсчитывают при технических расчетах не от абсолютного нуля, а от значения, соответствующего нулю стоградусной шкалы. Теплосодержание железа S при нагреве от 0 до 1600° возрастает на 1434 кал/г. В критических точках, соответствующих аллотропическим превращениям Feα→ Fer (906°) и Fer —>Feα (1401°), а также температуре плавления (1528°), при нагреве поглощается, а при охлаждении выделяется теплота, и теплосодержание изменяется скачкообразно. Теплоемкость твердого тела (истинная или при данной температуре) с ватт/г°С представляет предел отношения количества теплоты ∆S, сообщенного телу, к соответствующему изменению температуры ∆Т при бесконечном уменьшении этого изменения с=dS/dT. Для расчетов иногда удобно принимать среднюю теплоемкость в данном промежутке температур, представляющую отношение количества теплоты S2—S1, сообщенного телу, к соответствующей разности температур T2—T1. Так, например, средняя теплоемкость железа в промежутке от 0 до 1500° составляет 256/1500=0.73 ватт/г С°. Так как в сварочных процессах масса свариваемого металла изменяется несущественно удобно в расчетах использовать удельную объемную теплоемкость, численно равную произведению массовой теплоемкости на плотность. Дифференциальное уравнение теплопроводности Связь между величинами, участвующими в передаче теплоты теплопроводностью, устанавливается так называемым дифференциальным уравнением теплопроводности, на основе которого строится математическая теория теплопроводности. В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии, сочетаемый с законом Фурье. Выделим в теле некоторую часть объема V, ограниченную замкнутой поверхностью S, через которую происходит тепловое взаимодействие выделенной части с окружающей ее средой — остальной частью тела. Имеет место следующее утверждение: количество теплоты Q, полученное выделенным объемом за время dt вследствие теплопроводности, а также от внутренних источников теплоты, равно изменению внутренней энергии вещества, содержащегося в выделенном объеме: Q = Q1 + Q2. (2.13) где Q — изменение внутренней энергии вещества, содержащегося в выделенном объеме V за время dt, Дж; Q1 — количество теплоты, введенное в выделенный объем путем теплопроводности за время dt, Дж; Q2 — количество теплоты, которое выделилось в объеме V за время dt вследствие внутренних источников теплоты, Дж. Это утверждение вместе с
законом Фурье положено в основу вывода
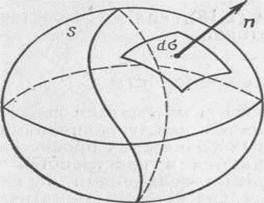
Рис. 2.5 Пусть V — выделенный объем произвольной формы части тела, ограниченный замкнутой поверхностью S (не обязательно изотермической); n — единичный вектор внешней нормали к точкам поверхности S (рис. 2.5); Т(х, у, z, t) — температура тела в точке (х, у, z) в момент времени t. Вычислим общее количество теплоты Q, полученное выделенным объемом за малый промежуток времени dt, имея в виду, что Q=Q1+Q2. Для вычисления Q1 воспользуемся законом Фурье в скалярной форме. Количество теплоты, подведенное в выделенный объем через элементарную площадку dσ за время dt, равно dQ1 =λ∂T/∂n·dσ·dt = λ·n·gradT dσ· dt =- qndσ·dt (2.14) где q =— λ grad T—вектор плотности теплового потока. Количество теплоты, протекающее за время dt через площадь поверхности S, выразится интегралом где qn — проекция вектора q на нормаль п. Поверхностный интеграл (2.15) можно преобразовать в объемный по формуле Остроградского — Гаусса, связывающей двойной интеграл по поверхности S с тройным интегралом по объему V, ограниченному этой поверхностью:
Таким образом,
Выделение или поглощение теплоты внутри объема V удобно хаpактеризовать с помощью плотности (мощности) тепловых источников. Под плотностью тепловых источников понимают такую функцию F(x, у, z, t), когда в элементарном объеме dV за промежуток времени dt выделяется количество теплоты, равное dQ2= F(x, у, z, t)dVdt= F(M, t)dVdt. (2.18) Тогда за промежуток времени dt в теле объемом V выделится количество теплоты
Здесь F(M, t)>0; если F(M, t)<0, то теплота не выделяется, а поглощается; функция F(M, t) считается непрерывной и ограниченной. Общее количество теплоты Q,, полученное выделенным объемом V,
С другой стороны, согласно формуле (2.13), это количество теплоты равно изменению внутренней энергии вещества, содержащегося в выделенном объеме. Указанное изменение на основании первого закона термодинамики может быть выражено формулой Q=CdT, (2.21) где С — теплоемкость выделенного объема; dT — изменение его температуры. Таким образом, Q может быть вычислено двумя способами, с одной стороны, по формуле (2.20), с другой путем учета изменения температуры в точках объема V, ограниченного поверхностью S. В точке (х, у, z) за промежуток времени dt температура Т(х, у, z, t) изменится на Т(х, у, z, t+dt)-T(x, у, z, t)=(dT/dt)dt. Элементу объема dV массой ρdV для такого изменения температуры потребуется количество теплоты, равное cρ (dT/dt)dVdt, а всему объему
где с—удельная теплоемкость, Дж/(кг-град); ρ — плотность вещества, кг/м3; ср, Дж/(м3-град). Принимая во внимание (2.21) с учетом (2.20) и (2.22), находим
Равенство (2.23) должно выполняться для любой части тела объемом V. Это возможно только тогда, когда в каждой точке внутри тела cρ(∂T/∂t) + divq – F(M,t) = 0 (2.24) Это заключение справедливо, если левая часть в равенстве (2.24) — непрерывная функция. Предположим, что в точке М(х, у, z) равенство нарушается, т. е., например, [cpdT/dt+divq—F(M, t)]>0. Тогда, интегрируя обе части неравенства по некоторой области V, содержащей точку М, получим противоречие с условием (2.23). Так как q=—λgradT, то равенство (2.24) можно записать следующим образом: cp(dT/dt)=div(λgvadT)+F(M, t). (2.25) Получено уравнение, которому должна удовлетворять функция Т(х, у, z, t), представляющая собой температуру некоторого тела. Это уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье. Для изотропного гомогенного тела параметры с, ρ, λ постоянные; далее, так кaк div(grad T)= ∆T, где ∆ — оператор Лапласа, то окончательно запишем дТ/∂t = а∆Т(М, t)+[1/(cp)]F(M, t), (2.26) где а= λ/(ср) коэффициент пропорциональности, называемый температуропроводностью, м2/ч. Тогда, в декартовых координатах уравнение (2.26) имеет вид dT/dt=a(∂2 T/ ∂x2 + ∂2T/∂y2 +∂2T/∂z2)+[1/(cp)]F(x, у, z, t). (2.27) В отличие от λ, которая характеризует теплопроводящую способность тела, а характеризует теплоинерционные свойства тела и является мерой скорости выравнивания температурного поля в рассматриваемой среде. Действительно, по определению, а=λ/(ср), где сρ — объемная изобарная теплоемкость. Отсюда температуропроводность а прямо пропорциональна теплопроводности λ и обратно пропорциональна аккумуляционной способности сρ вещества. Особенно наглядным становится физический смысл а в уравнении теплопроводности, когда отсутствует внутреннее тепловыделение и ∂T/∂t=a∆T(M, t). Зная вблизи точки М(х, у, z) зависимость температуры от координат, можно предсказать, как быстро будет нарастать (или спадать) температура в этой точке при переходе к следующему моменту времени. При этом, чем больше а (т. е. чем меньше сρ), тем пропорционально быстрее меняется во времени температура. Таким образом, а характеризует способность вещества изменять с большей или меньшей скоростью свою температуру во времени. Уравнение (2.26) представляет собой дифференциальное уравнение в частных производных, в котором независимыми переменными являются время и три пространственные координаты, а зависимой переменной— функция Т (температура). Это уравнение первой степени (линейное), поскольку зависимая переменная Т входит в него только в первой степени. Но вместе с тем оно является уравнением второго порядка, так как дифференциальный оператор Т содержит производные второго порядка от Т по пространственным переменным. Функция F считается заданной функцией, в общем случае функцией координат и времени. Может, в частности, оказаться, что температура рассматриваемого тела в любой его точке не изменяется во времени, т. е. является функцией только координат (установившееся состояние). Тогда ∂T/∂t=0 и уравнение (2.26) принимает вид ∆T(M)+(1/λ)F(M)=0, (2.27) где плотность тепловых источников F (М) уже не зависит от времени. Уравнение (2.27) называется уравнением Пуассона. Если внутри тела отсутствуют тепловые источники и температурное поле стационарно, то имеем уравнение (в декартовых координатах) ∆Т(М)=∂2T/ ∂x2 + ∂2T/∂y2 +∂2T/∂z2 =0 , (2.28) которое называется уравнением Лапласа. |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


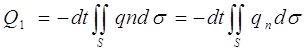 (2.15)
(2.15)