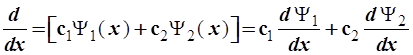|
Учебное пособие: Основные понятия и образы квантовой механикиУчебное пособие: Основные понятия и образы квантовой механикиВведениеВсякая наука, изучающая природные явления, использует некоторую систему образов, моделирующих реальные предметы, их качества и связи, существующие между ними. Модель и ее образы всегда выделяют лишь наиболее существенные черты явления. Чем удачнее образы, чем точнее и глубже подмечены связи между ними, тем, как правило, более экономны и даже скупы средства математического описания явлений и тем обширнее область, на которую могут распространяться методы теории. Одним из важнейших принципов естественнонаучной теории принято считать, так называемую "бритву Оккама", а именно: "не умножай число сущностей без надобности". Критерий истины в любой научной теории один – опыт, т.е. согласие теоретических прогнозов с результатами эксперимента. Одна из наиболее глубоких областей науки, очень несложная по применяемым математическим средствам, строгая и всеобъемлющая по своим выводам, – безусловно, термодинамика. Ее называют "королевой физики". Понятия термодинамики исторически оказали сильнейшее влияние на систему взглядов и образов квантовой механики. Не случайно великие умы ХХ-го века – Планк, Эйнштейн, Бор и многие другие – оставили неизгладимый след именно в этих разделах естествознания. Химическая наука неотделима от этих двух фундаментальных разделов физики. Квантовая механика изучает свойства отдельных частиц, и том числе атомов, молекул и кристаллов, рассматривая их как физические системы, образованные из ядер и электронов. Термодинамика делает следующий шаг, переходя от отдельных частиц к их коллективам. Эти физические системы, коллективы, принято называть термодинамическими системами. Разумеется, многие понятия и образы обеих дисциплин перекрываются. Пока частиц в системе относительно немного и есть возможность проследить за поведением каждой из них, используется аппарат квантовой механики. Но, если число частиц увеличивается настолько, что проследить за ними по отдельности становится невозможным, мы переходим к термодинамическому методу. Как правило, строгость теории связывают с возможностью ее математической формулировки и построением количественных критериев, которые можно было бы сопоставить с результатами экспериментальных измерений. На этой ступени развития и обобщения естественнонаучного знания ситуация наиболее точно передается словами переписки двух знаменитых ученых России – В.И. Вернадского и П.А. Флоренского: "Язык образов заменяется языком символов". Символы и их математическая связь являются эквивалентами физических образов, моделирующих явления природы на уровне элементарных частиц и их образований, таких как атомы, молекулы и кристаллы. Квантовая механика использует мощный математический аппарат, в основе которого лежит теория операторов; предметом анализа последней являются математические действия над функциями – операторы. Причины этого станут ясными по мере обсуждения теории. В каждой конкретной области естествознания используется свойственный ей минимальный набор образов, моделей и понятий, которые следует принять в качестве простейших, а прочие категории данной области науки будут конструироваться на их основе. В качестве исходных могут быть использованы разные системы образов, но они, всегда оказываются связанными между собой. Выбор исходных образов диктуется соображениями удобства, а подчас и просто вкусом исследователя. Эта ситуация прослеживается в классической механике. Так, системы уравнений Ньютона, Лагранжа, Гамильтона выводимы, и взаимозаменяемы. Так же обстоит дело и в термодинамике; например, существуют различные равносильные и взаимозаменяемые формулировки 2-го начала термодинамики. Такое же положение имеет место и в квантовой механике. Наша задача – выделить простейшие из ее категорий, которые достаточно рациональным способом позволяют рассматривать проблемы химии. 1.1. Состояния и уровни системы. Волновые функции 1.1.1. Квантово-механическая система – это одна частица или несколько частиц, взаимодействующих друг с другом и совершающих совместные движения, В классической механике одним из разделов является статика, которая рассматривает покоящиеся системы с взаимно неподвижными частями. В микромире, изучаемом методами квантовой механики, статические, покоящиеся системы немыслимы. Все частицы, образующие систему, – всегда в движении. Обсудим характер такого движения. 1.1.2. Проще всего это сделать для замкнутой устойчивой системы, не подверженной внешним воздействиям. Энергия такой системы постоянна, а частицы находятся в строгом периодическом движении. В атоме, например, электроны обращаются вокруг ядра; в молекуле ядерный остов совершает периодические движения – колебания и вращения, а электроны периодически движутся в поле ядер и т.д. При этом некоторая совокупность координатных характеристик периодически изменяется, но измерить мгновенные положения отдельных частиц в принципе невозможно, да в этом нет и необходимости. В то же время такие характеристики, как энергия, момент количества движения, частоты колебаний доступны для экспериментального определения с той или иной точностью. 1.1.3. Эта ситуация принципиально нова в сравнении с движением классических систем. В квантовом мире мгновенные координаты частиц и закон движения, как изменение этих координат во времени лишены смысла и их следует заменить иными понятиями. Важнейшее из таких понятий понятие состояния. Под этим непростым, но и не подлежащим упрощению, понятием подразумевается вся совокупность измеримых характеристик системы. 1.1.4. Неизменные во времени состояния замкнутых систем называются стационарными, а неизменные параметры таких состояний – динамическими характеристиками. Движения в стационарных состояниях замкнутых систем строго периодичны, а частоты таких движений – их важнейшие характеристики, становятся характеристиками состояний. 1.1.5. У замкнутых систем, образованных из двух и более частиц, полная энергия отрицательна по знаку. При этом за нуль энергии принимается потенциальная энергия взаимодействия частиц, бесконечно удаленных друг от друга. В устойчивых состояниях потенциальная энергия сил сцепления считается отрицательной, и по модулю она больше суммарной кинетической. Полную энергию стационарного состояния системы называют энергетическим уровнем, или просто уровнем. 1.1.6. Экспериментально установлено, что стационарные состояния замкнутых систем образуют дискретные наборы. Дискретны и уровни таких систем. Несколько разных состояний могут иметь одинаковую энергию. В таком случае говорят, что энергетический уровень вырожден. Кратностью вырождения уровня называется число состояний с равной энергией. 1.1.7. Дискретные состояния квантово-механической системы образуют счетные множества. Элементы этих дискретных наборов можно нумеровать. В качестве множеств, пригодных для нумерации состояний и уровней, обычно используют множество натуральных чисел N {1, 2, 3…}, или Zо {0,1,2,3...}, или множество целых чисел – Z {...-2, -1, 0, +1, +2...}. Не исключены и другие дискретные множества, например {...-3/2, -1/2, +1/2, +З/2...}. Важно то, что соседние элементы таких множеств отличаются на 1. 1.1.8. Один из уровней замкнутой системы обладает минимально возможной для ее устойчивого существования энергией. Этот уровень называют основным. Обычно с него и начинают нумерацию в порядке возрастания энергии. Остальные уровни, энергия которых больше основного уровня, называют возбужденными. 1.1.9. Если для нумерации уровней пригодны множества N или Zо, то для нумерации состояний иногда их может оказаться недостаточно. У систем, имеющих вырожденные уровни, состояния внутри таких уровней нуждаются в добавочной нумерации. Здесь-то обычно и приходят на помощь фрагменты множества Z или других множеств. 1.1.10. Для каждого из состояний
квантово-механической системы вводят свой математический образ и его символ.
Такой образ называют волновой функцией, для нее используют символ 1.1.11. Каждому состоянию отвечает свой энергетический уровень: Е1, Е2, Е3,…Еk,…. Множество разрешенных значений энергии образует спектр уровней системы:
У вырожденных уровней нумерация может быть изменена и дополнена благодаря группировке состояний по уровням. 1.1.12. Введем важные понятия состояний "чистых" и состояний "смешанных". "Чистые" – это дискретные состояния, которые разрешены для частиц, находящихся в стационарных условиях, т.е. не подверженных никаким внешним воздействиям. Такая ситуация идеальна. Реально всякая частица (атом, молекула и т.п.) лишь одна из многих, входящих в термодинамическую систему образца. Последнюю обычно рассматривают в состоянии теплового равновесия, которое в простейшем случае поддерживается за счет соударений, т.е. обмена энергией и состояниями между отдельными частицами. Поэтому приходится ожидать, что всякое реальное состояние квантово-механической системы "смешанное" и включает в себя любое из возможных "чистых" состояний с вероятностью, которая определяется условиями теплового равновесия. 1.1.13. Часто волновую функцию состояния называют вектором состояний. Это связано с особенностями математического аппарата и обусловлено глубокой аналогией, существующей между векторами и волновыми функциями. 1.2. Приборы и измерения. Операторы. Операторные уравнения 1.2.1. Исходная физическая информация о природных явлениях, в том числе и такая; которая служит первоосновой для построения теории, всегда исходит лишь из результатов эксперимента. Важнейшей чертой научного опыта является количественное измерение характеристик исследуемых систем. Соответственным образом организуется последовательность действий, приводящая к численному значению измеряемой величины. Материальная система, обеспечивающая процедуру измерения, – это прибор, имеющий определенную конструкцию с необходимыми взаимосвязанными узлами. Из стандартных узлов можно составить комбинацию различной сложности и конечного назначения. 1.2.2. В классической физике, связанной с изучением макроскопических объектов, процесс измерения можно организовать так, что измерение никак не сказывается на состоянии системы. В таком случае говорят, что измерение не возмущает объект. Так, вряд ли имеет смысл исследовать влияние астрономических наблюдений за планетами на их движение. 1.2.3. В квантовой механике, изучающей микромир, все обстоит иначе. Ни один из способов наблюдения и измерения не свободен от воздействия прибора на изучаемый микрообъект. При этом обязательно имеет место взаимодействие микрочастиц измерительного узла (фотонов, электронов и т.п.) и микросистемы[1]. Таким образом, элементарный акт измерения микроскопичен, но конечная информация выводится из детектирующего, узла прибора в преобразованном макроскопическом виде. 1.2.4. Отсюда ясно, что в акте измерения два материальных объекта – изучаемая система и прибор – образуют единое целое. Этим определяются необходимые математические образы, используемые в квантовой механике. Следом за волновой функцией – образом состояния системы, требуется ввести еще два образа, а именно: образ измерительного устройства и образ процедуры измерения, увязывающей систему и прибор в эксперименте 1.2.5. Измерения суть операции действия над системами. Естественно их образами считать также действия математические преобразования, определенные над волновыми функциями, то есть операторы. Измеряемые характеристики разнообразны, и приборы, как известно, специализированы, но имеется несколько типов фундаментальных величин и соответствующих им измерений, которые отображаются операторами простейшего вида. О них речь пойдет ниже. 1.2.6. Численные характеристики изучаемого состояния квантово-механической системы являются и целью, и итогом измерения. Акт измерения не оставляет состояние системы неизменным. После него может произойти релаксация – возвращение системы в исходное состояние, но может совершиться переход в другое состояние, либо иные превращения. Все зависит от способа постановки эксперимента. В любом варианте представляет интерес лишь такая схема опыта, которая приводит к информации о предыстории системы, т.е. о состоянии, непосредственно предшествующем измерению. В процессе измерения выделим стадию исходную и завершающую, когда сигнал об измеряемой величине уже сформирован. Определим в этом процессе условно следующие элементы:
1.2.7. Переведем наши рассуждения на язык математики. Для наглядности разделим поле страницы на три части вертикальными линиями и слева опишем словами существо акта измерения, выделяя построчно его узловые компоненты, далее введем ил математические символы-образы и, наконец, дадим комментарии:
*Обычно опускается. 1.2.8. В итоге в качестве математического образа все измерительной процедуры получаем операторное уравнение:
Уравнения подобной структуры хорошо известны в математике. Это так называемые уравнения на собственные значения в матричной алгебре, а также в теории специальных функций, построенных в разделе некоторых типов дифференциальных уравнений. 1.3. Основные черты математического аппарата квантовой механики 1.3.1. Обсудим важнейшие черты операторного уравнения (1.1).
Оно предписывает общую алгебраическую схему описания физических свойств
стационарных систем в микромире. Эта схема требует, чтобы в качестве операторов
физических величин 1.3.2. Хорошо известно, что простейшее математическое описание периодических процессов достигается с применением алгебры комплексных чисел. Комплексное число С и комплексно-сопряженное с ним С* состоят из одинаковых действительных частей (Rе) и различаются по знаку мнимых частей (Im),
Произведение
Экспоненциальные функции с комплексными показателями имеют тесную связь с тригонометрическими функциями и широко распространены в описании пространственных и временных периодических процессов. Рассмотрим для примера сопряженные функции:
Легко видеть, что квадрат их модуля, равный их произведению, единичен:
Периодичность есть характерная черта стационарных движений в микросистемах, поэтому в квантовой механике широко используется комплексное представление волновых функций, особенно при описании движений, включая вращательную составляющую. 1.3.3. В то время как волновые функции и операторы могут иметь комплексную форму, это недопустимо для собственных чисел операторов в уравнении (1.1), которые изображают измеримые величины и поэтому должны быть только действительными. Из этого вытекает жесткое требование к математической конструкции операторов квантовой механики, сформулировать которое мы сможем несколько ниже. Очень важно, что не существует никаких математических или физических соображений, которые отдавали бы предпочтение числу или функции перец комплексно-сопряженным двойником. Они равноправны во всех расчетах, так как в конечном итоге приложения комплексных чисел и функций всегда связаны с их модулем. По этой причине уравнение (1.1) и ему комплексно-сопряженное выражение (1.4) физически эквивалентны:
Величина 1.3.4. Сформулируем условие
самосопряженности операторов. Выделим из операторных уравнений (1.1) и (1.4)
собственные значения
Вообще говоря, это дело вкуса и удобства. Важно далее всюду соблюдать оговоренные однажды правила математического синтаксиса. Правые части этих последних равенств равны:
Поэтому равны и левые, т. е. получаем равенство (1.5), которое выражает условие самосопряженности операторов, имеющих действительные собственные значения.
1.3.5. В формуле (1.5) представлена
функция
Обратим внимание читателя на то, что
процедура комплексного сопряжения оператора 1.3.6. Запись уравнений типа .(1,5) и
(1.6) можно упростить и одновременно придать им дополнительный смысл, используя
символы-скобки
где
Если в интеграл введем оператор, то получаем также символическое скалярное произведение
в котором вектор Таким образом, в этой записи очень многие важные интегралы квантовой механики оказываются просто скалярными произведениями различных бра- и кет-векторов. Формула (1.6) в бракет-символах приобретает вид:
1.3.7. Из условия (1.6) или (1.9)
вытекает чрезвычайно важное свойство собственных функций эрмитова оператора,
называемое свойством ортогональности. Поясним смысл этого определения. Для
этого рассмотрим две разные собственные функции эрмитова оператора, например, f
и g, которым отвечают разные ненулевые собственные числа
Образуем скалярные произведения
Из первого скалярного произведения вычтем произведение, комплексно-сопряженное второму, и с учетом (1.11) получим:
По определению эрмитова оператора получаем:
откуда следует:
Поскольку
Функции g и f, удовлетворяющие условию (1.14), называются ортогональными во всей области определения переменных по аналогии с ортогональными векторами, скалярное произведение которых равно нулю. 1.3.8. Ортогональный набор функций, эрмитова оператора очень удобен тем, что функцию, определенную на тех же переменных, можно разложить в ряд по набору. Таким образом, он может рассматриваться в качестве базисного набора, аналогичного набору ортогональных базисных векторов. 1.3.9. Такое разложение
представляется всегда в виде линейной комбинации. Например, если ортогональный
набор включает функции (f1, f2, f3,... fn,...),
Если выбираемый ортогональный набор ограничен, то ряд состоит из конечного числа слагаемых. Ортонормированные наборы собственных функций эрмитовых операторов представляют собой естественную основу для конструирования математических образов дискретных состояний физических систем. 1.3.10. Второе важное требование, которое предъявляется к операторам квантовой механики – это линейность. Линейным называют оператор, обладающий следующими свойствами:
где
Это негативные примеры. Напротив, операции умножения на некоторую функцию или число, дифференцирование и интегрирование отвечают линейности, т.е. подчиняются уравнениям
[1] Следует различать исследуемый образец, также приготовленный в макроскопической форме и изучаемую микросистему, одну из огромного множества в его составе. Возможность выделения отдельных микросистем – атомов, молекул и элементарных частиц достижима в современных экспериментах, но прибор довести до микроуровня нельзя, хотя современная микроэлектроника сделала серьезные шаги в этом направлении. |
|||||||||||||||||||||||||||||||||||||
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


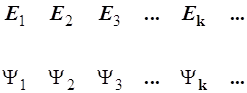
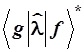 (1.9)
(1.9)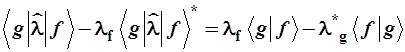 (1.12)
(1.12)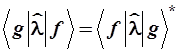 ,
, 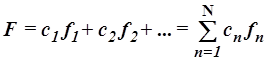 (1.15)
(1.15)