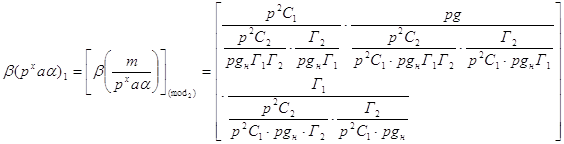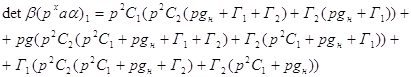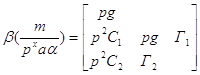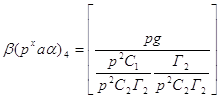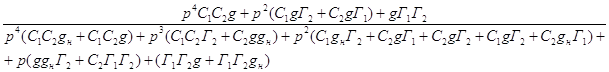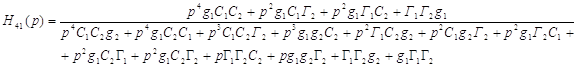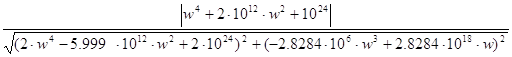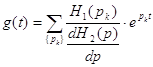|
Реферат: Анализ линейной динамической цепиРеферат: Анализ линейной динамической цепиМинистерство образования и науки Российской Федерации Южно - Уральский Государственный Университет Кафедра «Цифровые радиотехнические системы» Пояснительная записка к курсовой работе по курсу «Основы теории цепей» по теме «Анализ линейной динамической цепи» ЮУрГУ - К.21040062.10.27.000.ПЗ Нормоконтролер: Руководитель В.М. Коровин В.М. Коровин _______________ _______________ «____»___________ 2009г. «____»___________ 2009г Автор проекта: Студент группы ПС-210 Меркулов Д.А. «______»___________ 2009г. Проект защищен с оценкой ___________________ «_____»___________ 2009г. Подпись преподавателя: ______________________ Челябинск 2009 Аннотация Меркулов Д.А. Анализ линейной динамической цепи. Челябинск, ЮУрГУ, кафедра ЦРТС, 2009. 15с, 9 илл. Библиография литературы – 5 наименований. Исходя из цели работы и условий её выполнения, мною были получены все необходимые результаты (в виде графиков и формул). Все методы и этапы описаны в работе. Расчеты и построения графиков проводились в нескольких программах: MathCad 14, General Numbers.vi, MultiSim 10, Micro Cap 9, Exel. Курсовая работа состоит из пяти этапов. На первом этапе с помощью метода узловых напряжений получаем матрицу узловых проводимостей. На втором этапе – определяем комплексную функцию передачи, используя General Numbers.vi и метод обобщенных чисел. Этап третий – определяем нули и полюса комплексной функции передачи, построение карты полюсов и нулей. На четвертом этапе получены формулы и графики АЧХ, ЛАЧХ и ФЧХ. По этим графикам определяем крутизну среза (в дБ/дек) и время задержки сигнала в полосе задержания. Последний этап состоит в определении импульсной и переходной характеристик. Оглавление Введение 1. Электрическая схема фильтра 2. Нахождение комплексной функции передачи 3. Нахождение полюсов и нулей функции передачи. Карта полюсов и нулей 4. Построение АЧХ, ЛАЧХ, ФЧХ. Определение крутизны среза и времени задержки 5. Функции импульсной и переходной характеристик. Графики 5.1. Импульсная характеристика цепи 5.2. Переходная характеристика цепи Заключение Литература Введение В ходе выполнения курсовой работы необходимо: построить электрическую схему фильтра по указанным в таблице значениям; составить систему уравнений цепи в матричной и обычной формах; определить комплексную функцию передачи, перейти к операторной функции передачи; найти нули и полюса функции, построить карту полюсов и нулей; построить АЧХ, ЛАЧХ, ФЧХ, импульсную и переходную характеристики. В заключение курсового проекта необходимо отразить все аспекты выполнения тех или иных задач, сделать выводы в соответствии с полученными результатами и написать список литературы, которая была использована при выполнении работы. 1. Электрическая схема фильтра
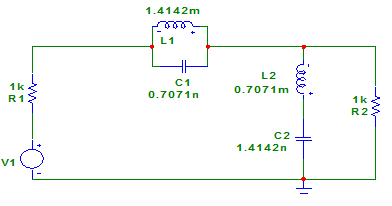
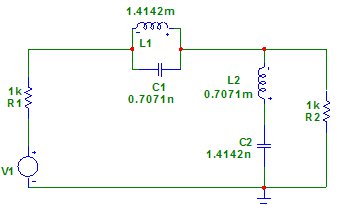
Рис 1. Схема фильтра. Базисным узлом примем узел с номером 0,который является заземленным. По методу узловых напряжений получаем матрицу:
Где Из матрицы составим систему уравнений в обычном виде:
2. Нахождение комплексной функции передачи Для нахождения комплексной функции передачи воспользуемся методом обобщенных чисел.
Рис 2. Схема фильтра для вычисления комплексной функции передачи. Составим проводимости узлов: 0: Y= 1: Y= Мы дополнительно ввели один узел между элементами L2 и C2. Диагональная матрица собственных проводимостей узлов
Получаем звездное число:
Напишем обобщенное число:
Далее определяем древесное число:
Определитель:
Числитель функции передачи:
Древесное число числителя:
Формула для вычисления функции передачи: H41(p)= Числитель:
Подставим все значения в формулу и поделим на p: H41(p)= Преобразуем обратно Г1 =1/L1 и Г2 =1/L2 Подставим все значения элементов в формулу H41(p),получаем:
Перейдем к нормированной частоте:
Для проверки и для того, чтобы удостовериться, что расчеты методом обобщенных чисел верны, воспользуемся результатом, полученным при использовании программы General Numbers.vi
где Как мы видим, функция передачи, полученная методом обобщенных чисел, полностью совпадает с функцией передачи, рассчитанной с помощью программы General Numbers.vi. 3. Карта полюсов и нулей По ранее найденной комплексной функции передачи цепи определим полюса и нули:
Для нахождения нулей выпишем отдельно числитель функции и приравняем его к нулю. Корни данного уравнения и будут являться нулями.
Решая данное уравнение, получим: p1,2,3,4= Для нахождения полюсов выпишем отдельно знаменатель функции и приравняем его к нулю. Корни данного полинома и будут являться полюсами.
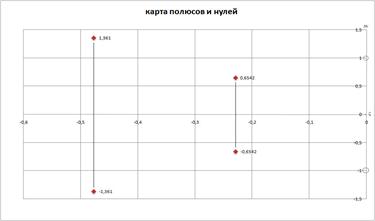
Решив данное уравнение, мы получили полюса: p1,2=-0.4775 p3,4=-0.2296
Рис 3. Карта полюсов и нулей. По полученным значениям построим карту полюсов и нулей: По виду карты полюсов и нулей можно определить некоторые особенности цепи: 1. Цепь является минимально-фазовой, т.к. в правой полуплоскости отсутствуют нули. 2. Цепь является устойчивой, т.к. в правой полуплоскости нет полюсов. 4. Нахождение функций АЧХ, ФЧХ и ЛАЧХ. Графики функций.
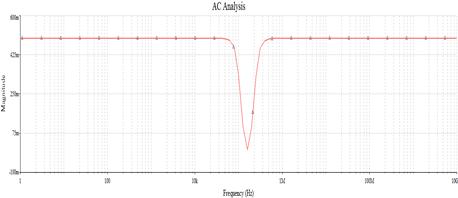
Рис 4. Амплитудно-частотная характеристика. Графики АЧХ, ФЧХ и ЛАЧХ построим с помощью программ MultiSim 10 и Micro Cap 9. Амплитудно-частотная характеристика (АЧХ) определяется как:
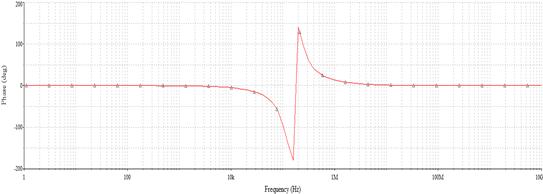
Рис 5. Фазо-частотная характеристика. Фазо-частотная
характеристика (ФЧХ) определяется как: По ФЧХ определяем время задержки сигнала:
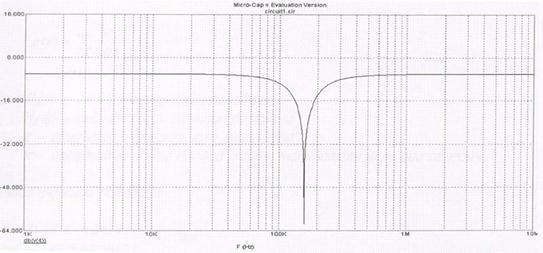
Логарифмическая АЧХ определяется как: 20*log(H(w))
Рис 6. Логарифмическая АЧХ. По графику определяем крутизну среза Sсреза=70 дБ/дек, что соответствует Sсреза =21 дБ/окт. 5. Импульсная и переходная характеристики. Графики характеристик 5.1 Импульсная характеристика цепи Импульсную характеристику посчитаем по формуле:
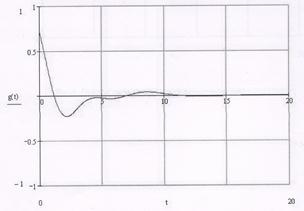
где H1(p) – числитель функции передачи; H2(p) – знаменатель функции передачи; e – основание натурального логарифма; k – порядковый номер полюса. Полюса функции передачи: p1= p2= p3= p4= H1=p4 + 2p2 + 1 H2=p4 + 2.8284p3 + 5.999p2 + 2.8284p + 2 g(t)=
Рис 7. График импульсной характеристики цепи. 5.2 Переходная характеристика цепи. Связь между импульсной и переходной характеристиками:
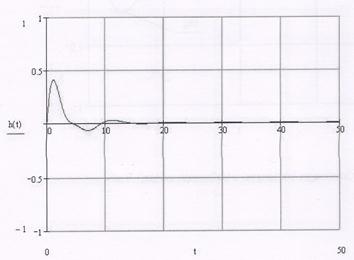
Получаем график:
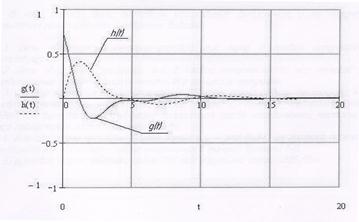
Рис 8. График переходной характеристики цепи. Для наглядности и сравнения приведем оба графика в одной системе координат:
Рис 9. Графики переходной и импульсной характеристик цепи. Заключение В ходе работы были проведены все необходимые вычисления и по полученным результатам можно сделать выводы: 1. Данный фильтр является полосно-задерживающим или режекторным. Об этом наглядно свидетельствует график АЧХ. 2. Цепь является устойчивой, т.к. в правой полуплоскости нет полюсов. Действительные части полюсов отрицательные, следовательно, все процессы затухают. 3. Цепь является минимально-фазовой, т.к. нули в правой полуплоскости отсутствуют. 4. Все свободные процессы в цепи затухают – это видно из графика переходной характеристики. 5. Крутизна
среза S=70
дБ/дек, время задержки сигнала У таких фильтров, чем резче разграничиваются друг от друга полосы непропускания, тем больше фильтрующее действие фильтра, тем больше его избирательность, тем лучше частотная характеристика фильтра – кривая зависимости тока через фильтр или его затухания от частоты. В случае идеального режекторного фильтра частотная характеристика имела бы вид прямоугольника. Литература 1. Коровин, В.М. Анализ линейных цепей с применением микрокалькуляторов: учебное пособие к курсовой работе. /В.М. Коровин – Челябинск: ЧПИ, 1988. 2. Стандарт предприятия. Курсовое и дипломное проектирование. Общие требования к оформлению. СТП ЮУрГУ 04-2001/Составители: Сырейщикова Н.В., Гузеев В.И., Сурков И.В., Винокурова Л.В., - Челябинск: ЮУрГУ, 2001. 3. Матханов, П.Н. Основы анализа электрических цепей: линейные цепи./П.Н. Матханов. – М: «Высшая школа», 1981. 4. Коровин, В.М. Схемотехническое проектирование. Теоретические основы: учебное пособие. Ч.2. / В.М. Коровин. – Челябинск: ЧГТУ, 1993. 5. Попов, В.П. Основы теории цепей./В.П. Попов. – Москва: «Высшая школа», 2003. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


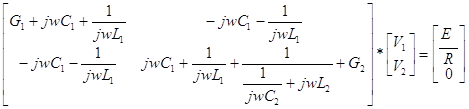
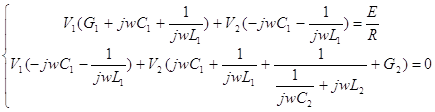
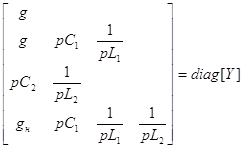
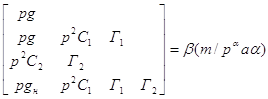
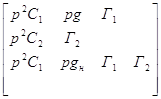 =
=