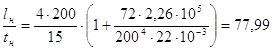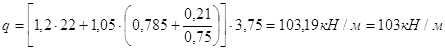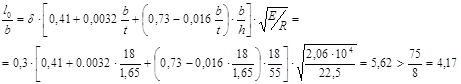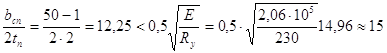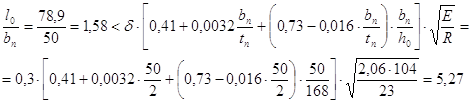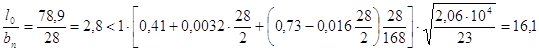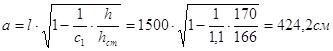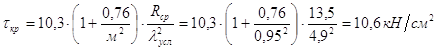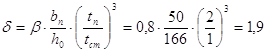|
Курсовая работа: Проект балочной площадкиКурсовая работа: Проект балочной площадкиМинистерство общего и профессионального образования РФ Кафедра строительных конструкций Курсовой проект по дисциплине "Металлические конструкции" 2009 г. Реферат В курсовом проекте выбрана схема проектируемой
балочной площадки; произведен расчет стального настила; подобраны и проверены
балки настила; рассчитана наиболее нагруженная главная балка площадки;
определены расчетные усилия и произведена компоновка сечения с наибольшим
изгибающим моментом и на расстоянии Произведена расстановка ребер жесткости и проверена местная устойчивость стенки. Рассчитана опорная часть балки, поясные швы. Произведен расчет монтажного стыка главной балки; наиболее нагруженной колонны; оголовка колонны; базы колонны. Все расчеты произведены в соответствии с нормативной документацией.
Содержание Исходные данные 1. Выбор схемы балочной клетки 2. Расчет стального настила 3. Компоновка балочной клетки 4. Определение высоты и размеров главной балки 5. Расчет соединения поясов со стенкой 6. Изменение сечения балки по длине 7. Правка местной и общей устойчивости элементов главной балки 8. Расстановка ребер жесткости 9. Расчет монтажного стыка главной балки 10. Расчет опорной части главной балки 11. Подбор и компоновка сечения сквозной колонны 12. Расчет базы колонны 13. Расчет оголовка колонны Литература Исходные данные 1. Шаг колонн в продольном направлении, А = 15 м. 2. Шаг колонн в поперечном направлении, В = 6 м. 3. Габариты площадки в плане, 3А×3В. 4. Отметка верха настила – 11 м. 5. Величина полезной нагрузки, р = 22 кН/м2. 6. Допустимый относительный прогиб настила 1/200. 7. Тип колонны: сквозная. 1. Выбор схемы балочной клетки Балочная клетка представляет собой систему пересекающихся несущих балок, предназначенных для опирания настила перекрытий. В зависимости от схемы расположения балок балочные клетки подразделяются на 3 типа: упрощенные, нормальные и усложненные. В упрощенной балочной клетке нагрузка от настила передается непосредственно на балки, располагаемые параллельно короткой стороне перекрытия, затем на вертикальные несущие конструкции (стены, стойки). В балочной клетке нормального типа балки настила опираются на главные балки, а те на колонны или другие конструкции. В усложненной балочной клетке балки настила опираются на вспомогательные, которые крепятся к главным балкам. Толщина настила зависит от полезной нагрузки: при полезной нагрузке 10 кПа – tн = 6 мм при полезной нагрузке 10 – 20 кПа – tн = 8 мм при полезной нагрузке более 20 кПа – tн = 10 мм. Тип балочной клетки выбирают путем анализа различных вариантов, сравнивая расход металла, технологические требования. 2. Расчет стального настила
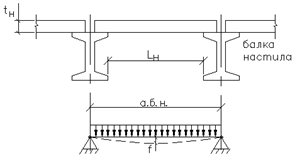
tн – толщина настила; f – прогиб; lн – допустимый пролет; а.б.н. – шаг балок настила При временной распределенной нагрузке 22 кПа принимаем толщину настила 10 мм. Толщина настила на изгиб с распором можно вычислить приближенно из условия заданного предельного прогиба по формуле:
Е1 – цилиндрическая жесткость настила. При коэффициенте Пуассона ν = 0,3 (для стали) Е1 определяется по формуле:
3. Компоновка балочной клетки Сравним 2 варианта компоновки балочной клетки: I вариант. Пролет главной балки делим на 19 промежутков по 78,9 см. Определяем вес настила, зная, что 1м2 стального листа толщиной 10 мм весит 78,5 кг.
Нормативная нагрузка на балку настила: qn = (pn + gn)·a = (22 + 0,785)·0,789 = 28,88 кН/м = 0,29 кН/см Расчетная нагрузка на балку настила: q = (np·pn +ng·gn)·a = (1,2·22 + 1,05·0,785)·0,789 = 21,48 кН/м Расчетный изгибающий момент для балки настила длинной 6 м:
Требуемый момент сопротивления балки:
Принимаем двутавр №30 по ГОСТ 8239–72, имеющий: I = 7080 см4, W =472, вес g = 36,5 кг/м, ширину полки 13,5 см. Проверяем на прогиб: f = (5/384)·ql4/EI
Принятое сечение балки удовлетворяет условиям прогиба и прочности, т. к. W = 597 см3 > Wтр = 390,5 см3. Общую устойчивость балок настила проверять не надо т. к. их сжатые пояса надежно закреплены в горизонтальном направлении приваренным к ним настилом. Определяем расход металла на 1м2 перекрытия: настил – 78,5 кг/м2, балки настила g/a = 42,2/0,789 = 53,5 кг/м2. Весь расход металла: 78,5 + 53,5 = 132 кг/м2 = 1,32 кН/м2.
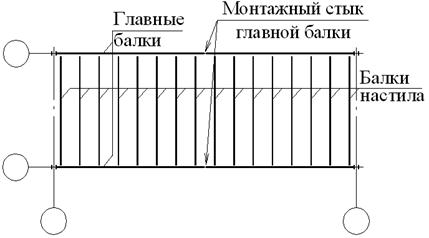
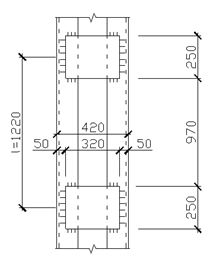
Рисунок 1 – Схема блочной клетки (нормальный вариант) II вариант (усложненная компоновка)
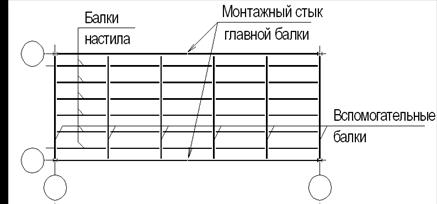
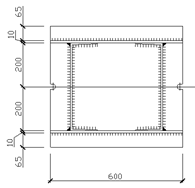
Рисунок 2 – Схема блочной клетки (усложненный вариант) Принимаем настил, как и в I варианте. Расстояние между балками настила а = 600/8 = 75 см < 78 см. Пролет балки настила l = 3,75 м. Нормативная и расчетная нагрузка на нее: qн = (22 + 0,785)·0,750 = 17,1 кН/м = 0,171 кН/см. q = (1,2·22 + 1,05·0,785)·0,75 = 20,42 кН/м Расчетный изгибаемый момент и требуемый момент сопротивления балки
Примем I 20, имеющий: I = 1840 см4, W = 184 см3, g = 21 кг/м. Проверяем только прогиб балки, т. к. W = 184 см3 > Wтр = 145 см3.
Принятое сечение удовлетворяет условиям прочности и прогиба. Определяем нормативную и расчетную нагрузку на вспомогательную балку:
Определяем расчетный изгибающий момент и требуемый момент сопротивления вспомогательной балки:
Принимаем I 55, имеющий: I = 55150см4; W = 2000 см3 ширину и толщину полки b = 18 см, t = 1,65 см, g = 89,8 кг/м Т.к. W = 2000см3 > Wтр = 1873 см3, проверяем балку на прогиб
Затем проверяем общую устойчивость вспомогательных балок в середине пролета, в сечении с наибольшими нормальными напряжениями. Их сжатый пояс закреплен от поперечных смещений балками настила, которые вместе с приваренным к ним настилом образуют жесткий диск. В этом случае за расчетный пролет следует принимать расстояние между балками настила l0 = 75 см. Исходя из условий формулы
при τ = 0 и с1 = с получаем
Подставляя значения δ в формулу, получаем:
Поскольку 5,62 > 4,17, принятое сечение удовлетворяет требованиям прочности, устойчивости и прогиба. Суммарный расход металла 78,5 + 21/0,75 + 89,8/3,75 = 133,455 кг/м2 По расходу материала I вариант выгоднее. 4. Определение высоты и размеров главной балки
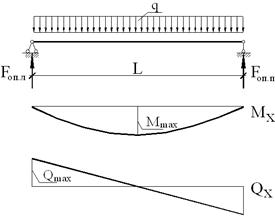
Рисунок 3 – Расчетная схема и усилия в главной балке
Найдем усилия:
Минимальная высота сечения сварной балки из условия жесткости при f/l =1/200 должна быть (см. с. 91 (II)): hmin/l = 1/30, откуда hmin = 1500/30 = 50 см При расчете по эмпирической формуле толщина стенки составит tст = 7 + 3·500/1000 = 8,5 мм. Принимаем таблицу стенки 10 мм (четного размера). Оптимальная высота балки при tст = 10 мм будет:
где k = 1,15 – для сварных балок. Назначаем высоту балки 170 см. Проверяем принятую толщину стенки из условия действия касательных напряжений: tст = 3Q/2hRsγc = 3·1275000/2·170·13500·1 = 0,8 см < 1 см, т.е. условие удовлетворяется. Проверяем условие, при соблюдении которого не требуется постановка продольных ребер в стенке
Принятая стенка толщиной 10 мм удовлетворяет прочности на действие касательных напряжений и не требует постановки продольного ребра для обеспечения местной устойчивости. Подбираем сечение сварной балки: I = W (h/2) = 20787·(170/2) = 1766895 см4 Iст = tст·hст3/12 = 1·(170 – 2tn)3/12 = 1·(170 – 2·2)3/12 = 381191 см4 – момент инерции стенки. где hст = h – 2tn = 170 – 2·2 = 166 см. tn = 2 см – принимаемая толщина полки. Момент инерции полок: In = I – Iст = 1766895 – 381191 = 1385704 см4. h0 = h – tn = 170 – 2 = 168 см – расстояние между центрами тяжести полок. Площадь сечения одной полки An = 2In/h02 = 2·1385704/1682 = 98 см2. Ширина полки bn = An/tn = 98/2 = 49 см. Принимаем сечение полок 500×20 мм. Проверяем принятую ширину (свес) поясов bn по формуле, исходя из обеспечения их местной устойчивости:
условие удовлетворяется тоже, при упругопластической работе сечения балки
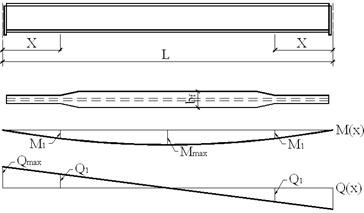
где hcn = h – 2tn = 170 – 2·2 = 166 см. Проверяем принятое сечение на прочность Фактический момент инерции I = (tст – hст3/12) + 2a2An = (1·1663/12) + 2·842 ·100 = 1792391 см4, где a = h0/2 = 168/2 = 84 см. Фактический момент сопротивления W = I/(h/2) = 1792391/85 = 21087 см3. Напряжение по формуле составит σ = M/W = 4781·105/21087 = 226,7 < 230 МПа = Ryγc, условие удовлетворяется. Проверяем касательные напряжения по нейтральной оси сечения у опоры балки τ = QS/Itст = 1275000·11844/1792391·1 = 8425 Н/см2 = 84 МПа < Rsγc = =135 МПа. где S – статический момент полусечения S = An·(h0/2) + (Aст/2)·(hст/4) = 100·84 + (1·166·166/2·4) = 11844 см3 Полная площадь сечения баки А = 166·1 + 2·100 = 366 см2 Масса 1 м балки (без ребер жесткости): а = 366·100 (7850/106) = 287 кг/м, а с ребрами жесткости 1,03·287 = = 296 кг/м. 5. Расчет соединения поясов со стенкой Сдвигающее усилие Т, приходящееся на 1 см длины балки составит: T = τ·tст =QSn/I = 1275·8400/1792391 = 6 кН, где Sn – статический момент пояса (сдвигаемого по стыку со стенкой) относительно нейтральной оси: Sn = An·(h0/2) = 10·84 = 8400 см3. Сдвигающая сила Т воспринимается двумя швами, тогда минимальная толщина этих швов при длине lw = 1 см, будет kf ≥ QSn/n·I·(βRw)·γc = T/2·(βRw)·γc = 6000/2·1·1·16200 = 0,185 см, где (βRw) – меньшее из произведений коэффициента глубины проплавления (βf или βz) на расчетное сопротивление, принимаемое по условному срезу металла на границе сплавления шва (Rwzγwz); при γwt = γwz = = 1 и для автоматической сварки проволокой d = 2 мм марки СВ – 08А (по ГОСТ 2246 – 70*) βf = 0,9 имели βfRwfγwf = 0,9·180·1 = 162 МПа. Принимаем конструктивно минимальную толщину шва kf = 7 мм, рекомендуемую при толщине пояса 17 – 22 мм (см. табл. 3.3. с. 62 [II]). 6. Изменение сечения балки по длине
Рисунок 4 – К изменению сечения по длине Место изменения сечения принимаем на расстоянии 1/6 пролета от опоры. Сечение изменяем уменьшением ширины поясов. Разные сечения поясов соединяем сварным швом встык электродами Э42 без применения физических методов контроля. Определяем расчетный момент и перерезывающую силу в сечении: x = l/6 = 15,6 = 2,5 м M1 = [qx·(l – x)]/2 = [170·2,5·(15 – 2,5)]/2 = 2656 кН·м = 265600 кН·см Q1 = q·(l/2 – x) = 170·(15/2 – 2,5) = 850 кН Определяем требуемый момент сопротивления и момент инерции измененного сечения исходя из прочности сварного стыкового шва, работающего на растяжение:
Определяем требуемый момент инерции поясов (Iст = 381191 см4) In1 = I1 – Iст = 1154725 – 381191 = 773534 см4 Требуемая площадь сечения поясов An1 = 2In1/h01 = 2·773534/1682 = 54,8 см2 Принимаем пояс 280×20 мм, An1 = 56 см2 Принимаемый пояс удовлетворяет рекомендациям bn1 > 18 см, bn1 >170/10 = 17 cм Определяем момент инерции и момент сопротивления уменьшенного сечения: I1 = Iст + 2b1tn·(h0/2)2 = 381191 + 2·28·2·(168/2)2 = 1171463 cм4 W1 = 2I1/h = 2·1171463/170 = 13782 cм3 σmax = M1/W1 = 265600/13782 = 19,3 кН/см2 < Rсв = 0,85·23 = 19,55 кН/см2
7. Проверка общей и местной устойчивости элементов главной балки 1) Проверка прочности балки. Проверяем максимальные нормальные напряжения в поясах в середине балки: σ = Mmax/C1W = 478100/1,1 = 20,6 кН/см2 < R = 23 кН/см2 Проверяем максимальное касательное напряжение в стенке на опоре балки:
Проверяем местные напряжения в стенке под балкой настила σm = F/tст·lм =128,88/1·17,5 = 7,36 кН/см2 < R, где F = 2·21,48·6/2 = 128,88 кН – опорные реакции балок настила lм = b + 2tn = 13,5 + 2·2 = 17,5 см – длина передачи нагрузки на стенку банки. Проверяем приведенные напряжения в месте изменения сечения балки (где они будут максимальны):
где
Проверки показали, что прочность балки обеспечена. 2) Проверяем общую устойчивость балки в месте действия максимальных нормальных напряжений, принимая за расчетный пролет l0 – расстояние между балками настила в середине пролета балки, где учтены пластические деформации:
где В месте уменьшенного сечения балки (балка работает упруго и δ = 1)
Проверки показали, что общая устойчивость балки обеспечена. 3) Проверка прогиба не производится, так как h = 170 > 50 см = hmin
Рисунок 5 – Схема монтажного стыка главной балки 8. Расстановка ребер жесткости Определяем необходимость постановки ребер жесткости:
λст = 2,2 – при действии местной нагрузки на пояс балки. Вертикальные ребра жесткости необходимы. Кроме того, в зоне учета пластических деформаций необходима постановка ребер жесткости под каждой балкой настила, т. к. местные напряжения в стенке в этой зоне не допустимы. Определяем длину зоны использования пластических деформаций в стенке по формуле:
Определяем средние значения М и Q на расстоянии х = 157,9 см. от опоры под балкой настила M2 = [qx·(l – x)]/2 = [170·1,579 (15 – 1,579)]/2 = 1801 кН·м = 180100 кН·см Q = q·(l/2 – x) = 170·(15/2 – 1,579) = 1006,5 кН Определяем действующие напряжения:
где W = 20787 см3 из определения высоты и размеров главной балки.
σм = 7,36 кН/см2 (из расчета балки на устойчивость) Определяем критические напряжения:
где h0 = hcт, λусл = λст = 4,9
Размеры отсека a1/h0 = M = 0,95 и δм/σ = 7,36/8,46 = 0,86
По таблице 7.6. (с. 158 [I]) при δ = 1,9; a/h0 = 0,9 предельное значение σм/σ = 0,109 Расчетное значение σм/σ = 0,86 > 0,109 σкр определяем по формуле:
где скр = 33,1 по табл. 7.4 (с. 155 [I]) при δ = 1,9 Определяем σмкр
где с1 = 11 по табл. 7.5 (с. 156 [I]) при δ = 1,9 a1/2hст = 157,9/2·166 = 0,47 Подставляем все значения в формулу
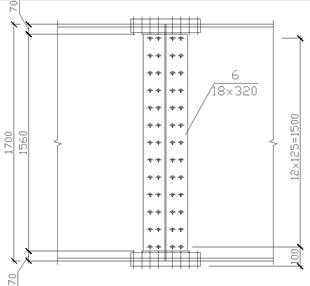
Устойчивость стенки обеспечена и постановка ребер жесткости на расстоянии а1 = 157,9 см возможна. Определяем размеры ребер жесткости ширина bp = hст/30+40 = 1660/30 + 40 = 95 мм Примем bp = 120 мм толщина Примем tp = 7 мм 9. Расчет монтажного стыка главной балки
Рисунок 6 – Схема опорной части главной балки Стык делаем в середине пролета балки, где М = 4781 кН·м и Q = 0. Стык осуществляем высокопрочными болтами d = 20 мм из стали «селект», имеющий по таблице 6.2
где
т. к. разница в номинальных диаметрах отверстия и болта больше 1 мм; М = 0,42 и γн = 1,02; Принимая способность регулирования натяжения болта по углу закручивания, k = 2 – две плоскости трения. Стык поясов. Каждый пояс балки перекрываем тремя накладками сечениями 500×12 мм и 2×220×12 мм, общей площадью сечения An = 1,2·(50 + 2·22) = 112,8 см2 > An = 100 см2 Усилие в поясе определяем по формуле: Mn = MIn/I = 4781·1385704/1792391 = 3696 кН·м Nn = Mn/h0 = 3696/1,68 = 2200 кН где I, In, h0 – из расчета главной балки Количество болтов для прикрепления накладок рассчитываем по формуле: n = Nn/QВБ = 2200/132 = 16,6 Принимаем 16 болтов. Стык стенки. Стенку перекрываем двумя вертикальными накладками сечением 320×1560×8 мм. Определяем момент, действующий на стенку Мст = MIст/I = 4781·381191/1792391 = 1016 кН·м Принимаем расстояние между крайними по высоте рядами болтов: amax = 1660·2·80 = 1500 Находим коэффициент стыка
Из таблицы 7.8 (с. 166 [I]) находим количество рядов болтов по вертикали k. при Принимаем 13 рядов с шагом 125 мм. Проверяем стык стенки по формуле:
Проверяем ослабление нижнего растянутого пояса Ап.нт = 2,0·(50 – 2·5,785) = 86,86 см2 > 0,85 Аn = 0,85·100 = 85 см2 Ослабление пояса можно не учитывать. Проверяем ослабление накладок в середине стыка четырьмя отверстиями
Принимаем накладки толщиной 18 мм
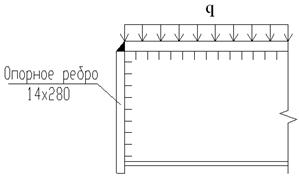
10. Расчет опорной части главной балки Опорная реакция балки F = 1275 кН Определяем площадь смятия торца ребра
где Rсм.т. = 35,5 кН/см2 = 355 МПа (прил. 4 [I]). Принимаем ребро 280×14 мм, Ар = 28·1,4 = 39,2 см2 >35,9 см2. Проверяем опорную стойку балки на устойчивость относительно оси Z. Ширина участка стенки, включенной в работу опорной стойки:
Аст = АР + tcт·bст = 39,2 + 1·19,45 = 58,65 см2 Iz = 1,4·283/12 + 19,45·13/12 = 2562 cм4
λ = hст/iz = 166/6,6 = 25,1 по приложению 7 (I) φ = 0,947
Рассчитываем прикрепление опорного ребра к
стенке балки двусторонними швами полуавтоматической сваркой проволокой СВ
– 08Г2. Предварительно находим параметры сварных швов и определяем
минимальное значение β βш = 0,9; βс = 1,05 βш· Определяем катет сварных швов по формуле:
Принимаем швов kм = 7 мм. Проверяем длину рабочей части шва: lм = 85·βс·kм = 85·1,05·0,7 = 62,5 см < hcт = 166 см Ребро привариваем к стенке по всей высоте сплошными швами. 11. Подбор и компоновка сечения сквозной колонны Постоянная нагрузка от собственного веса колонны – 1,5 кПа. Расчетное усилие в стержне колонны: N = 1,01·(np·p + ng·g) ·A·B = 1,01·(1,2·22 + 1,05·1,5) ·15·6 = 2540 кН Длина колонны: l0 = 11 – 0,01 – 0,3 – 1,72 = 8,97 м Зададимся гибкостью λ = 60 и находим φ = 0,785 (по прил 7 [1]), площадь сечения Aтр = N/(φ·R) =2540/0,785·28 = 115,5 см2, где R = 28 кН/м2 – расчетное сопротивление для стали марки Вст 3nc6 – 2 радиус инерции: imp = l0/λ = 897/60 = 14,95 По сортаменту ГОСТ 8240 – 72* принимаем два швеллера 40 со значениями А = 2·61,5 = 123 см3; ix = 15,7 см. Рассчитываем гибкость относительно оси х λх = 897/15,7 = 57; φх = 0,800 (прил. 7) Проверяем устойчивость относительно оси х σ = N/φA = 2540/0,8·123 = 25,8 кН/м2 < R = 28 кН/см2
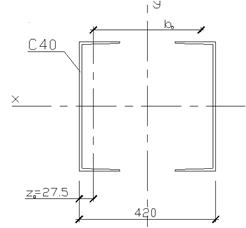
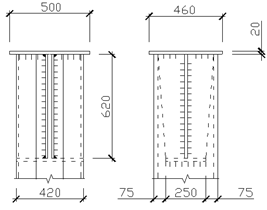
Рисунок 7 – Сечение сквозной колонны Расчет относительно свободной оси. Определяем расстояние между ветвями колонны из условий равноустойчивости колонны в двух плоскостях λпр = λх, затем требуемую гибкость относительно свободной оси у-у по формуле:
Принимаем гибкость ветви равной 30 и находим Полученной гибкости соответствуют радиус инерции iy = 897/48 = 18,7 см; и требуемое расстояние между ветвями b = i·y/0,44 = 18,7/0,44 = 42 см Полученное расстояние должно быть не менее двойной ширины полок швеллеров плюс зазор, необходимый для оправки внутренних поверхностей стержня bтр = 2·115 + 100 = 330 мм < 42 см, следовательно принимаем ширину колонны = 420 мм. Проверка сечения относительно свободной оси. Из сортамента имеет: I1 = 642 см4; i1 = 3,23 см; z0 = 2,68 см. Iy = 2·[642 + 61,5·(21 – 2,75)2] = 42250 см4 Расчетная длина ветви lb = λ1·i1 = 30·3,23 = 97 см Принимаем расстояние между планками 97 см м сечение планок 10×250 мм, тогда Iпл = 1·253/12 = 1302 см4 Радиус инерции сечения стержня относительно свободной оси
Гибкость стержня относительно свободной оси λу = 897/18,5 = 48,5 Для вычисления приведенной гибкости относительно свободной оси надо проверить отношение погонных жесткостей планки и ветви Iпл/b0: I1/lв = Iпл·lв/I1b0 = 1302·122/642·36,5 = 6,7 >5 Здесь b0 = 42 – 2·2,75 = 36,5 см – расстояние между ветвями в осях. Приведенную гибкость вычисляем по формуле при отношении погонных жесткостей планки и ветвей более 5.
Т.к. λпр = λх, напряжение можно не проверять, колонна устойчива в двух плоскостях.
Рисунок 8 – К проверке сечения относительно свободной оси Расчет планок Расчетная поперечная сила: Qусл = 0,27А = 0,27·123 = 33,21 кН Поперечная сила, приходящаяся на планку одной грани. Qпл = Qусл/2 = 33,21/2 = 16,6 кН Изгибающий момент и поперечная сила в месте прикрепления планки Мпл = Qпл·lb/2 = 16,6·122/2 = 1012 кН·см Fпл = Qlb/ba = 16,6·122/36,5 = 55,5 кН Принимаем приварку планок к полкам швеллеров угловыми швами с катетом шва kш = 0,8 см.
Необходима проверка по металлу шва. Расчетная площадь шва Ауш = kш·lш = 0,8·(25 – 2·0,8) = 18,72 см2 Момент сопротивления шва Wш = kш·l2ш/6 = 0,8·(25 – 2·0,8)2/6 = 73 см3 Напряжение в шве от момента и поперечной силы: σуш = Мпл/Wш = 1012/73 = 13,86 кН/см2 τуш = Fпл/Ауш = 55,5/18,72 = 2,9 кН/см2 Проверяем прочность шва по равнодействующему напряжению:
Размеры планки 320×250×10 12. Расчет базы колонны Требуемая площадь плиты из условия смятия бетона найдем по формуле:
где Rсм.б = γ·Rb, для В 12,5 => Rb = 7,5 МПа: γ = 1,2 Rcм.б. = 1,2·7,5 = 9 МПа Принимаем плиту размером 55×60 см Апл = 55×60 = 3300 см2; σф = N/Aпл σф = N/Aпл = 2540/3300·10-1 = 7,7 МПа < Rсм.б = 9 МПа Толщину плиты принимаем из расчета отдельных участков. М = σф·а2/2 = 770·92/2 = 31185 Н·см = 0,31 кН·м Проверим работу среднего участка плиты 1, заключенного между ветвями и опертыми по четырем сторонам. Отношение сторон составит b/a = 404/400 = 1,01 Требуемый момент сопротивления сечения плиты составит W = M/Ryγc = = 31185/20500 = 1,52 см3, где Ry = 205 МПа – при толщине листов 21 – 40 мм. При толщине табл. 5.5 (с. 137 II) вычисляем изгибающие моменты для полос шириной 1 см Ма = α1·σф·а2 = 0,05·770·402 = 61600 Н·см Мв = α2·σф·а2 = 0,048·770·402 = 59136 Н·см при b/a = 1,01; α1 = 0,05; α2 = 0,048 Требуемую толщину плиты определяем по Ма:
Принимаем плиту толщиной 40 мм. Высота листов траверсы: h = N/βf·kш·Rушγс·nш = 2540000/0,7·1·18000·1·1·4 = 50,3 см где kш = 10 мм, n = 4 – число швов. Принимаем высоту траверсы = 50 см. Анкерные болты принимаем конструктивно диаметром 24 мм. Размеры фундамента в плане принимают на 15 – 20 см в каждую сторону от опорной плиты. LФ×ВФ = 80×90 см
условие прочности фундамента соблюдаются. Глубина заделки анкеров диаметром 24 мм должна быть не менее 850 мм.
Рисунок 9 – Схема базы колонны 13. Расчет оголовка колонны
Рисунок 10 – Схема оголовка колонны Принимаем толщину опорной плиты оголовка 20 мм. При kш = 0,8 см, высота ребра составит: hp = N/4βf·kш·Rуш·γуш·γс = 2540000/4·0,7·0,8·18000·1·1 = 62 см. Принимаем высоту ребра 62 см. Длина ребра lp = 320 мм = z lp = 28 + 2 + 2 = 32 см Толщина ребра: tp = N/lp·Rs = 2540000/0,32·33200 = 2,4 см Принимаем tp = 25 мм Rs = 332 МПа z – расчетная длина распределения местного давления опорных ребер балки. Проверяем напряжение в швах, прикрепляющих ребра оголовка к плите при kш = 12 мм. σ = N/βf·hш·Σlш = 2540000/0,7·1,2·154 = 19635 Н/см2 = 196,35 МПа < < Rуш·γуш·γс = 200 МПа, где Σlш = 2·42 + 2·(40 – 5) = 154 см Ветви колонны приваривают к опорной плите швами толщиной 6 – 8 мм. Размер плиты оголовка назначаем конструктивно 500×460 мм. Литература 1. Металлические конструкции. Учебник для вузов. Под редакцией Е.И. Беленя – М.: Стройиздат, 1986 г. 2. Примеры расчета металлических конструкций. Учебное пособие для техникумов. Мандриков А.П. – М.: Стройиздат, 2001 г. 3. Методические указания. Сост. И.В. Слепнев. Краснодар, 2006 г. |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


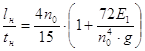 где
где