|
Курсовая работа: Вплив процесів деформування на поверхневий шар металівКурсовая работа: Вплив процесів деформування на поверхневий шар металівМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Національний університет «Львівська політехніка» Кафедра «Технології машинобудування» Курсова робота: “ Вплив процесів деформування на поверхневий шар металів ” Дисципліна: Наукові дослідження Виконав: Ст. гр.____ ___________ Викладач ___________ Львів – 2009р. Зміст Вступ. 1. Процес формування верхнього шару металу в умовах пружної і пластичної деформації. 2. Зміни РВЕ на поверхні металів при деформуванні. 3. Дослідження структурних змін і зарядового рельєфу поверхні при втомі металевих матеріалів. 4. Закономірності формування енергетичного рельєфу металевої поверхні при контактних взаємодіях і при механічній обробці. Висновки Література Вступ Одним з центральних напрямків розвитку фізики твердого тіла, фізики металів є дослідження особливостей будови металевої поверхні та вивчення змін в її структурі і властивостях у процесі деформування. Найважливішими задачами цих досліджень є вивчення взаємозв'язку змін в іонній та електронній підсистемах металу, визначення закономірностей формування та еволюції напружено - деформованого стану поверхневого шару матеріалу в різних умовах деформування. В роботі досліджується процес деформування поверхневого шару металів і визначення впливу деформації на характеристики напружено - деформованого та енергетичного стану поверхні. Особливий стан приповерхневого шару вимагає також розробки спеціальних експериментальних методів визначення деформаційних характеристик. Для дослідження закономірностей поверхневого деформування в даній роботі удосконалені і використані методи вимірювання роботи виходу електронів (РВЕ), контактного електричного опору (КЕО), вимірювання залишкових макроскопічних і мікроскопічних напруг, визначення механічних характеристик поверхневого шару. На основі отриманих експериментальних даних у роботі розвинуті фізичні уявлення про закономірності змін в іонній і електронній підсистемах металів у процесі деформування. Актуальність теми. Наукова актуальність дослідження властивостей поверхневих шарів металів полягає в необхідності розвитку уявлень про фізичну природу деформування і руйнування реальних металевих матеріалів, розкритті механізму процесів, що відбуваються у приповерхневому шарі. Для встановлення фізичних механізмів деформаційних процесів і побудови відповідних теоретичних моделей, насамперед, необхідні експериментальні дослідження. Сучасні знання про фізичні і механічні характеристики приповерхневої області металів і про взаємозв'язок їх з властивостями, що характеризують міцність, розрізнені і недостатні. Практично не досліджено взаємозв’язок енергетичного стану поверхні із змінами структури приповерхневої області. Зростаючий інтерес до вивчення фізичних і механічних властивостей приповерхневих шарів металів в останні роки, крім наукової мети, обумовлений важливими технічними застосуваннями. Прикладна актуальність проблеми визначається практично усіма задачами, що виникають при деформуванні металів і сплавів у процесі їх виробництва та експлуатації. На даний час розроблені і застосовуються на практиці різні види зміцнюючих обробок, метою яких є забезпечення необхідних властивостей поверхні. Для оптимізації існуючих способів і вдосконалення технології зміцнення необхідна розробка експериментальних методів досліджень механічних властивостей приповерхневої області, вивчення закономірностей формування оптимальних структур, розвиток фізичних моделей, що адекватно відображають особливості протікання деформаційних процесів поблизу поверхні матеріалу. Важлива для практики проблема надійності і довговічності, наприклад, літальних апаратів, багато в чому визначається напруженим станом приповерхневого шару деталей, здатністю його протистояти розвитку процесів втоми і контактного деформування. З цієї причини в даній роботі одним з об'єктів досліджень були сплави, що використовуються для виробництва газотурбінних двигунів (ГТД). Методи дослідження: - вимірювання розподілу КРП по поверхні для аналізу змін енергетичного стану в процесі деформування; - прецизійна рентгенівська дифрактометрія для визначення параметрів напружено - деформованого стану і структурних змін; - вимір КЕО для визначень напружень і деформацій при контактних взаємодіях. - випробування на кінетичне індентування для визначення фізичних параметрів деформування приповерхневої області; - електронна мікроскопія для встановлення змін дислокаційної структури; - випробування на тертя та опір втомі під впливом знакозмінних напружень, як критерій формування оптимальної кристалічної структури; - теоретичний аналіз досліджених явищ. Наукова новизна одержаних результатів 1. Вперше встановлені закономірності розподілу РВЕ по поверхні деформованих металів. У пластичній області спостерігається падіння РВЕ, причому більшому ступеню деформації відповідає більш значне зменшення РВЕ. При досягненні певного ступеня деформації РВЕ досягає граничного значення. Виявлений деформаційний енергетичний рельєф зумовлений виходом на поверхню дислокацій. Таким чином, методом РВЕ фіксується кінетика виходу дислокаційних ліній на вільну поверхню. Результати розрахунків лінійної густини деформаційних диполів в залежності від деформації збігаються за порядком величини з густиною слідів ковзання дислокацій. 2. Вперше розроблена нова самоузгоджена розрахункова схема РВЕ, що враховує істотні для поставленої задачі поправки до фізичної моделі “желе”: дискретність розподілу позитивного заряду; вплив релаксації іонних площин поблизу поверхні кристалу на електронний розподіл на межі металу; вплив діелектричного середовища, що граничить з поверхнею металу. Показано, що з ростом пружної деформації кристалічних ґраток концентрація електронів за межею металу спадає повільніше. Виявлено, що вплив діелектричного середовища додатково знижує величину густини електронів поблизу поверхні. 3. На основі уявлень про взаємозв'язок РВЕ і електровід’ємності атомів, а також даних скануючої тунельної мікроскопії, запропоновано нову фізичну модель і спосіб розрахунку РВЕ в залежності від параметрів пружно-пластичного деформування. Обчислення, проведені для алюмінію і міді, показали задовільне узгодження з експериментальними даними. 4. Вперше встановлено закономірності зміни РВЕ при знакозмінному деформуванні металів і сплавів. Виявлено, що зародження мікротріщин втоми відбувається на ділянці поверхні з максимальною попередньою зміною РВЕ. На основі встановленого фізичного механізму запропоновано кількісну модель кінетики структурних перетворень на поверхні металів, що включає рух дислокацій під впливом знакозмінних навантажень, вихід дислокацій на поверхню і появу заряджених сходинок, наслідком чого є зміна РВЕ. Метод вимірювання розподілу РВЕ по поверхні дає можливість прогнозувати зародження мікротріщин втоми вже на ранніх стадіях випробувань. 5. Досліджено вплив електроімпульсної обробки металів на квазістаціонарний деформований стан приповерхневих шарів. Вплив обробки імпульсним струмом проявляється в зниженні рівня макронапружень у приповерхневому шарі, збільшенні мікроскопічних напружень і в зменшенні розміру блоків кристалічної мозаїки. Показана можливість помітного збільшення опору втомі сплавів на основі титана у результаті електроімпульсної обробки за рахунок “прицільного” відпалу дефектів кристалічних ґраток і створення більш рівноважної структури біля поверхні. 6. У рамках молекулярно-динамічного моделювання термічної дії електроімпульсної обробки показано, що термічний пік навіть з не дуже високою максимальною температурою (~1000 0С) може приводити до “залікування” області кристала, яка містить дефекти типу вакансія-міжвузельний атом. Знайдено, що термічні коливання атомів активізують процес рекомбінації дефектів, направлено-орієнтуючий вплив забезпечується пружними полями дефектів.. Електроімпульсна обробка сплавів титана забезпечує підвищення міцності втоми на 25¸50 %. Розроблений на рівні винаходу новий спосіб магнітно-абразивної обробки, поліпшує якість обробки поверхні, значно збільшує довговічність деталей. 1. Процес формування верхнього шару металу в умовах пружної і пластичної деформації Проведений літературний аналіз уявлень про залежність РВЕ від параметрів пружно-пластичного стану металів показує що у навантаженому кристалі енергія може запасатися не тільки в кристалічних ґратках, але і в електронній підсистемі. У зв'язку з цим актуальними є дослідження структури і фізичних властивостей приповерхневої області металів, обумовлених прикладеними силами, що приводять до пружних і пластичних деформацій. Зроблено висновок, що створення фізичної картини деформування металів потребує експериментальних досліджень взаємозв'язку іонної і електронної підсистем деформованих металів і розробку теорії розвитку специфічних процесів, що відбуваються у приповерхневих шарах металів і сплавів. Розробка експериментальної техніки і методики досліджень. Для систематичного дослідження фізичних процесів, що відбуваються у відносно тонких приповерхневих шарах металевих матеріалів, необхідно було створити і використовувати адекватну експериментальну техніку. Прагнення до коректності висновків про взаємодію двох підсистем у металі при деформації вимагало комплексного методичного підходу до досліджуваних явищ. У більшості випадків для забезпечення надійних результатів необхідно було також забезпечити удосконалення цих методів з метою суттєвого підвищення точності, локальності і продуктивності вимірів. Була розроблена експериментальна установка, призначена для вимірів РВЕ з можливістю одночасного проведення іспитів металевих зразків на втому, установка містить малогабаритний п'єзоелектричний вібростенд і комплекс вимірювальної апаратури. Величина РВЕ вимірювалася методом динамічного конденсатора Кельвіна. Випробування зразків на втому виконувались методом дискретного навантаження. Була вдосконалена методика вимірів КРП на основі аналізу залежності КРП від напруги компенсації з одночасною комп'ютерною обробкою результатів вимірів. Виконані дослідження впливу зовнішнього середовища на РВЕ. Встановлено, що рівномірне ультрафіолетове опромінення поверхні металевого зразка викликає зміщення кривих розподілу РВЕ як цілого, без зміни їхньої геометрії. Створення більш високих поверхневих енергетичних рівнів зменшує вплив адсорбційних процесів на РВЕ, що підвищує точність і відтворюваність результатів вимірів. Застосування ультрафіолетового опромінення у процесі вимірів дозволяє вивчати залежність РВЕ саме від деформаційних процесів. Похибка вимірів РВЕ не перевищувала 1 меВ. Дослідження внутрішніх напружень і параметрів кристалічної структури здійснювались за допомогою рентгенівського дифрактометра ДРОН-3М. Було досягнуто збільшення граничного можливого подвійного кута Вульфа-Брегга до 177,60 за рахунок зміни положення детектора розсіяного випромінювання і застосування нової колімуючої системи. Похибка виміру макроскопічних напружень, яка була розрахована для робочих значень кутів досліджуваних об'єктів при використанні монохроматичного Kb випромінювання, зменшилася приблизно в 10 разів. Для визначення мікроскопічних напружень і розміру блоків кристалічної мозаїки був використаний метод гармонічного аналізу форми рентгенівських ліній. Оскільки для розрахунку залишкових макронапружень необхідні дані про пружні константи, був розроблений рентгенодифрактометричний метод визначення модуля Юнга і коефіцієнта Пуассона приповерхневої області металів, оснований на вимірюванні деформації при іспитах зразків прямокутного перерізу на трьохточковий згин. Розроблені і виготовлені установки для електроімпульсної (ЕІО) і магнітно-абразивної (МАО) обробки зразків і деталей. Для одержання достовірних даних при побудові графіків, використовувалася статистична обробка результатів вимірів. Об'єктом досліджень у даній роботі були матеріали, які відносяться до трьох різних класів: алюміній (99,99 %); сплави на основі титана марок ВТ3-1, ВТ8 і ВТ9; жароміцні сталі марок ЕП866 (15Х16К5Н2МВФАБ), ЕП499 (15Х16Н2АМ), ЕІ698 ХН73БТЮ), жароміцний ливарний сплав на нікелевій основі марки ЖС6К (ХН67ДО5В5М4ЗЮ6). Вибір алюмінію обумовлений значною величиною КРП, що зменшувало відносну похибку вимірів і давало можливість порівнювати одержані результати з літературними даними. При вивченні контактних деформацій і зносу використовувалися зразки міді і сплави системи Fe-C-B. 2. Зміни РВЕ на поверхні металів при деформуванні Використання методу сканування по всій поверхні зразка при механічних випробуваннях дозволило одержати обґрунтовану інформацію про механізми зарядової перебудови поверхні. Методика дослідження полягала в одновісному деформуванні зразків з полікристалічного алюмінію з постійною швидкістю з одночасним виміром РВЕ в контрольованих точках поверхні. Перехід до стадії пластичного деформування викликає характерне зменшення РВЕ. При цьому більшому ступеню деформації в робочій області зразка відповідає більша зміна РВЕ. На різних стадіях деформування навантаження припинялося і вимірювався розподіл РВЕ уздовж обраних ліній робочої поверхні зразків. Характерна крива зміни напруження σ із підвищенням ступеня деформації і відповідні значення роботи виходу Ф представлено на рис.2. Видно, що плавному зростанню розтягуючого напруження, відповідає падіння РВЕ. Навпаки, релаксація напружень приводить до зростання РВЕ. В області пластичного деформування було виявлено зміну РВЕ, викликану релаксаційними процесами (відпочинок зразка) при вимиканні розтягуючого пристрою. На основі експериментальних даних встановлено, що має місце як швидка релаксація РВЕ порядку 0,02 еВ між послідовними навантаженнями, так і повільна релаксація порядку 0,1 еВ, реалізована протягом 12¸15 годин без зняття навантаження. Важливо відзначити існування граничного значення РВЕ. Починаючи з деякої деформації e = 0,05, величина РВЕ істотно не зменшується, рис.3. У процесі відпочинку “енергетичний деформаційний рельєф” частково згладжується. При повторних вимірах РВЕ після відносно великих проміжків часу, спостерігався характерний зсув кривої розподілу як цілого. Як показали додаткові дослідження, за зміну геометрії кривих розподілу РВЕ по поверхні відповідають структурні процеси, а зсув кривих обумовлений адсорбційними перебудовами під впливом зовнішнього середовища. Результати дослідження закономірностей зміни роботи виходу Φ по поверхні пластично деформованих металів дозволили одержати такий вираз для зміни РВЕ:
де α - безрозмірний параметр деформування; e - відносна деформація; e0 - відносна деформація, що відповідає початку пластичної течії матеріалу. Елементарний акт пластичної деформації, як відомо, пов'язаний з виходом на вільну поверхню дислокаційної моноатомної сходинки. Вже в об`ємі кристалу перерозподіл електронів навколо дислокації приводить до утворення електричного дипольного моменту. Таким чином, можна говорити про перенос дислокаційних диполів на вільну поверхню при деформуванні. При виході на поверхню дислокація не тільки зберігає свій дипольний момент, але і збільшує його за рахунок зниження ефекту екранування електронів провідності. З іншого боку, відома залежність РВЕ від густини моноатомних сходинок на поверхні кристала [1]:
де P - дипольний момент на одиницю довжини поверхневої сходинки; n - густина сходинок; q - заряд електрона; ε0 - електрична стала. Результати розрахунку за формулами (1) і (2) лінійної густини диполів в залежності від деформації збігаються за величиною з густиною тонких слідів ковзання для деформованого алюмінію за даними електронної мікроскопії. При дослідженні деформаційних процесів методом РВЕ важливим моментом є те, що фіксується кінетика виходу дислокацій на вільну поверхню металу. Початкова ділянка зміни РВЕ при пластичній деформації визначається формуванням смуг ковзання. Коли ж в основному смуги ковзання визначені і локалізовані, пластичне деформування визначається рухом дислокацій по вже сформованим лініям ковзання і утворення нових дислокаційних диполів практично не відбувається. В результаті, РВЕ виходить на насичення і при подальшому деформуванні не змінюється. У цьому ж розділі дисертації на основі методу функціонала електронної густини розглянуті теоретичні уявлення про залежність РВЕ від деформації металів. Автором запропонована нова самоузгоджена розрахункова схема. При її розробці в модель “желе” були введені поправки. Ці поправки пов'язані з дискретністю розподілу позитивного заряду та враховують вплив релаксації іонних площин поблизу поверхні кристала на електронний розподіл на границі металу, а також вплив діелектричного середовища, що граничить з поверхнею металу. Задача розв`язувалась визначенням мінімуму поверхневої енергії σ як функціонала двох варіаційних параметрів β і λ:
де 1/β - являє собою характерну товщину поверхневого шару поблизу границі металу, на якій різко змінюється електронна густина; λ - зсув поверхневої густини іонів відносно об'ємного положення. При розрахунку були використані пробні функції розподілу електронної густини на границі металу у вигляді:
Значення релаксаційних параметрів β і λ, що відповідають мінімуму поверхневої енергії, надалі використовувались для розрахунку роботи виходу:
Тут Ф0 - складова РВЕ в моделі “желе”; Ф1 - псевдопотенціальний внесок у РВЕ з урахуванням релаксації гратки. У розглянутій моделі вплив деформації на РВЕ враховувався зміною об`єму елементарної комірки та параметром псевдопотенціалу. Загальною особливістю кривих є збільшення РВЕ з ростом пружної деформації, що погоджується з результатами експериментальних досліджень. Аналіз деформаційної залежності РВЕ для різних кристалографічних площин алюмінію свідчить про те, що зростання РВЕ визначається зміною як об'ємної складової РВЕ, так і поверхневої. Як видно із рис.4, нехтування гратковою релаксацією, приводить до істотно іншої деформаційної залежності РВЕ, але зберігається основна тенденція зростання РВЕ. Насамперед, це проявляється в нелінійності кривих, одержаних із врахуванням релаксації. Розрахунки також показали, що пружне деформування кристалічних ґраток приводить до більш повільного зменшення електронної густини за межею металу. При цьому діелектричне середовище додатково знижує цю величину. Вплив середовища полягає у “витягуванні” електронів з металу, а відповідно до приведених розрахунків, у результаті деформування ще більша кількість електронів переходить з металу в діелектричне середовище. Те, що поверхня при цьому стає більш негативно зарядженою, прямо свідчить про збільшення РВЕ. Робота виходу є чутливим індикатором структурної перебудови на поверхні металу. Оскільки експериментально розподіл РВЕ вимірюється для реальних металевих поверхонь, то в теоретичних моделях необхідно враховувати мікроскопічні поверхневі дефекти на атомному рівні. Зміни РВЕ, викликані структурними неоднорідностями на металевій поверхні, найбільш просто і правильно описує модель взаємозв'язку РВЕ із електровід`ємністю атомів [2]. На основі уявлень про нейтральну орбітальну електровід`ємність (НОЕ), пропонується новий метод розрахунку РВЕ в залежності від параметрів пружно-пластичного деформування. Об'ємна частина РВЕ залежить від енергії Фермі даного металу і дуже слабо змінюється при деформуванні. Поверхнева складова РВЕ може зазнавати значних змін при деформаціях, тому що вона визначається локальними поверхневими стрибками потенціалів, варіації яких залежать від мікрогеометрії і координації поверхневих атомів. Визначення мікрогеометрії деформуємої поверхні і координації поверхневих атомів стало можливим на основі останніх досягнень скануючої тунельної мікроскопії [3]. Виявлено, що деформаційні процеси на поверхні визначаються формуванням і еволюцією нанодефектів. Ці нанометричні дефекти мають форму призм різних розмірів, стінки яких утворюються за рахунок виходу на поверхню дислокацій по площинам легкого ковзання. Утворення дислокаційних сходинок на поверхні змінює електростатичний поверхневий бар'єр і, відповідно, РВЕ. Для моделювання задавалися значення відносної деформації. При цьому різні кристалографічні площини відрізняються кількістю розірваних зв'язків для найближчих і наступних сусідів. З урахуванням перерозподілу заряду при пружному деформуванні подвійного електричного шару, було отримано вираз для розрахунку РВЕ:
Тут З метою оцінки можливостей розробленої фізичної моделі був виконаний розрахунок залежності РВЕ від часу випробування на одномірне розтягування міді при трьох різних швидкостях деформування, рис.5. Розрахунок проведено з урахуванням кінетики формування ансамблів нанодефектів в процесі пластичного деформування. У програму обчислень була закладена часова осциляція концентрації нанодефектів. Було виявлено, що падіння РВЕ при пластичному деформуванні в основному визначається формуванням поверхневих дефектів першого рангу [3]. Осцилюючий характер еволюції поверхневих дефектів і вихід на плато змін РВЕ, що експериментально спостерігається, при граничних пластичних деформаціях викликає необхідність врахування впливу дефектів 2, 3 і 4 рангів. Вплив останніх на РВЕ виявляється в компенсації приросту РВЕ, викликаного зменшенням кількості дефектів 1 рангу. Порівняння розрахункових значень із експериментальними даними показало гарну відповідність. 3. Дослідження структурних змін і зарядового рельєфу поверхні при втомі металевих матеріалів Проведені виміри значень РВЕ в осьових напрямках зразків, що випробовувалися знакозмінними напруженнями по консольному типу. Дослідження процесу втоми дозволило вперше зробити висновок про існування двох основних стадій структурних змін в кристалічних ґратках поверхневого шару металів: початкова стадія зворотних структурних перебудов, коли величина РВЕ для даної точки поверхні періодично зменшується і збільшується, коливаючись поблизу деякого середнього значення; друга стадія незворотних структурних змін в поверхневому шарі, коли РВЕ в даній точці монотонно зменшується аж до руйнування зразка. Таким чином, на початкових стадіях впливу знакозмінних механічних напружень РВЕ осцилює поблизу деякого значення, що свідчить про зворотність до певного часу процесу накопичення дефектів кристалічної ґратки і про чергування процесів зміцнення - релаксації на цій стадії. В процесі циклічних деформацій на формування енергетичного рельєфу основний вплив має зміна структури металу. Розглядаючи тільки кристалографічні фактори, можна вважати, що до зменшення РВЕ приводить утворення на поверхні заряджених атомних сходинок. Відомо, що при циклічному навантаженні металів активізується вакансійний механізм деформування. Тому на початковій стадії ще можливе згладжування атомарної шорсткості за рахунок притоку вакансій з поверхні. Якщо джерелом цих вакансій будуть підвалини атомарних сходинок, то такий процес, у кінцевому рахунку, еквівалентний поверхневій дифузії. Це приводить до заповнення поверхневих впадин матеріалом поверхневих виступів. Тоді за зростання (відновлення значень) РВЕ в період обернених перебудов відповідає поверхнева дифузія, стимульована циклічними напруженнями. РВЕ зменшується в тих областях, де прикладені найбільші механічні напруження. З ростом числа циклів виділяються дві характерні ділянки на кривих розподілу РВЕ по поверхні. Перша пов'язана із пластичним деформуванням матеріалу поверхневого шару в зоні максимальних напружень. Важливими особливостями цієї ділянки є локалізованість падіння РВЕ і насичення РВЕ при визначеному наробітку (при певної кількості циклів). Друга ділянка безпосередньо прилягає до першої і відповідає росту РВЕ. Досліджено вплив проміжної відновлюючої термічної обробки на довговічність жароміцних сталей. Отримано, що проведення відбудовного відпуску після іспитів, що складають 20 - 30 % середньої довговічності, є перспективним способом, який дозволяє істотно збільшити довговічність. Методом дифракційної електронної мікроскопії досліджені зразки зі сталі ЕП479 після випробуваня на богатоциклову втому при температурі 20 і 500 oС. Структура стали ЕП479 після загартування і відпалу являє собою мартенсит, що складається з пакетів рівнобіжних пластин з високою густиною дислокацій. По границі та усередині первинних зерен аустеніту спостерігали виділення карбідної фази. Аналіз дифракційних картин і темнопольного зображення показав, що це частки типу Ме23C 6, розміром 0,2 - 0,5 мкм. Спостерігалася фрагментація мартенситних пластин. Виявлено, що під дією циклічного навантаження відбувається взаємодія дислокацій з утворенням субзернистої структури. Напружений стан поблизу границь збільшується скупченням дислокацій. Підгорнуті до границь дислокації створюють локальну концентрацію напруг, що може бути провісником утворення субмікротріщин. Перешкодою для переміщення дислокацій є частки фаз, які присутні у сталі. Якщо усередині зерна виділення цих часток відіграють позитивну роль - затримують рух дислокацій до границь, то виділення карбідної фази по границях зерен підсилюють напруженість границь, що сприяє появі субмікротріщин. Не тільки частки фаз перешкоджають переміщенню дислокацій, але й утворення субзеренної структури приводить до більш рівномірного розподілу дислокацій. Знайдено, що під дією циклічного навантаження спостерігається фрагментація мартенситних пластин у структурі сталей, взаємодія дислокацій, їх часткова анігіляція і утворення субзернистої структури. Більшій міцності втоми сталей відповідає відносно однорідна дрібна субструктура. Якщо металевий зразок зазнає циклічних напружень, то, як відомо, відбувається генерування дислокацій. Цей процес починається при напруженнях, які перевищують певне граничне напруження τs:
де μs - модуль зсуву; b - вектор Бюргерса; n - кількість дислокацій у скупченні; ρ0 - початкова густина дислокацій. Народжені дислокації під впливом зовнішніх змінних напружень рухаються в перетинаючих системах ковзання. Частина з них виходить на поверхню. У результаті виходу дислокацій на поверхню утворюються поверхневі сходинки. Ці сходинки несуть електричний заряд і, отже, утворюють електричні диполі. Внесок дислокаційних диполів приводить до зменшення РВЕ. Отримано наступне рівняння для зміни густини дислокацій в процесі випробувань матеріалу на втому:
де ρ - густина дислокацій; δ - коефіцієнт розмноження дислокацій; V0 – коефіцієнт пропорційності; U0 - енергія активації руху дислокацій; τm·sin(ω·t) - змінне напруження; tso і tsf початковий і кінцевий моменти дислокаційного руху в межах напівперіоду відповідно; k - стала Больцмана; T - температура. Рівняння (8) було розв`язане чисельно за допомогою ПК для різних значень амплітуди прикладеної напруженості. Густина дислокацій у поверхневому шарі була обчислена для кожного циклу. Результати обчислень густини дислокацій для алюмінію приведено на рис. 8.. Відповідність між експериментальними точками і теоретичною кривою задовільна. Збільшення густини дислокацій супроводжується зменшенням РВЕ. Збільшення РВЕ через збільшення густини сходинок може бути представлено формулою (2). Тоді, густина формування сходинок за цикл визначається густиною дислокацій і швидкістю їх руху:
Із експериментальних даних залежності РВЕ від кількості циклів наробки при випробуваннях алюмінію на знакозмінний згин було отримано dn/dN=318 сходинок × цикл-1 × см-2, що узгоджується з літературними даними 4. Закономірності формування енергетичного рельєфу металевої поверхні при контактних взаємодіях і при механічній обробці У
роботі було досліджено залежність контактної провідності 1/R від величини
навантаження N у процесі навантаження і розвантаження контактного з'єднання. Також
показані залежності, отримані при кінетичному індентуванні різних ділянок
поверхні зразка з міді марки М1 за різними режимами навантаження (статичне –
“С”; із впливом вібрації – “Д”) і для двох поверхонь: вихідної – “1” і “2” –
поверхні, що зазнали стиску за межею течії. На основі регресійного аналізу
встановлено, що отримані залежності
і характеризує вплив профілю опорної кривої шорсткуватої поверхні на величину фактичної площини контакту (ФПК). При індентуванні поверхні, зміцненої попереднім плоским стиском, злам залежностей не спостерігається. Таке поводження можна пояснити тим, що при індентуванні не зміцненої поверхні до настання пластичного насичення на зростання ФПК істотньо впливає деформація мікровиступів шорсткості. Після
досягнення пластичного насичення ФПК росте завдяки збільшенню контурної площі.
У присутності вібрації на вихідній поверхні швидкість росту ФПК і контактної
провідності істотно збільшується. В умовах циклічного навантаження відбувається
знеміцнення матеріалу, зумовлене підвищеною рухливістю дислокацій поблизу
поверхні. При індентуванні з накладенням вібрації в контактній зоні кінетика
контактних деформацій визначається, очевидно, конкуренцією процесів зміцнення і
знеміцнення. У випадку ж наявності залишкових напружень на вершинах
мікровиступів шорсткості на ріст ФПК переважний вплив має збільшення контурної
площі на всьому протязі контактного навантаження. Нелінійний характер ФПК від
навантаження в цьому випадку обумовлений зміцненням нижчих шарів. Відсутність
помітного впливу вібрації на нахил залежності Рентгеноструктурне дослідження
вихідної поверхні і після деформування стисканням, виявило наявність на них
однакових стискуючих залишкових напружень σ = -180 МПа, обумовлених
технологічною передісторією матеріалу зразків. Як відзначалося вище,
залежності, отримані при кінетичному індентуванні, свідчать про розходження
залишкових напружень у поверхневому шарі. Це протиріччя викликане тим, що
додаткові напруження зосереджені, головним чином, у вершинах мікровиступів
шорсткості, у той же час рентгенівську дифракцію одержано від більш товстого
шару (близько 100 мкм). З приведених даних випливає, що зміна КЕО при
кінетичному макроіндентуванні відчутна до величини залишкових напружень у
тонкому приповерхньому шарі, а саме, до інтегральної мікротвердості
шорсткуватого шару - параметру, що безпосередньо визначає кінетику контактної
взаємодії. У процесі поступового зняття навантаження відбувається пружне
відновлення області контактного деформування. Тому дослід розвантаження
становить інтерес для визначення пружних властивостей матеріалу і легше
піддається теоретичному опису. Із рішення задачі Герца для пружного зіткнення
двох тіл нами був отриманий вираз для ФПК і контактної провідності, у якому ці
величини пропорційні N1/2. При розгляді залежності Як показали проведені нами дослідження, значення максимальних змін РВЕ при контактних деформаціях і при деформуванні за схемою розтягування-стискання для тих самих металів збігаються. Розглянемо характерні закономірності змін РВЕ, що були викликані обробкою алюмінію шліфуванням. Підготовка зразків полягала в поліруванні поверхні і наступному відпалі у вакуумі при температурі (250 ± 3) 0С протягом чотирьох годин. Потім на п'ятьох ділянках зразка поверхня шліфувалася шкірками різної зернистості. Відповідні значення Ra(мкм) складали:1-1,5; 2-0,9; 3-0,45;4-0,21;5-0,075. Було виявлено, що перехід від більш грубого до більш дрібного шліфування супроводжується зменшенням РВЕ (ділянки 1,2 і 3), рис.10. Подальше зменшення параметра шорсткості поверхні приводить до зростання РВЕ (ділянки 4 і 5). Ділянка 3 відповідає змінам, що гранично досягаються РВЕ при пластичному деформуванні алюмінію. Зростання РВЕ пов'язане із зміною характеру поверхневого деформування при тонкому шліфуванні. Також було виявлено, що і релаксаційні процеси розвиваються по-різному для ділянок з різним шліфуванням. Для перших двох ділянок з відносно грубим геометричним рельєфом спостерігалось швидке відновлення вихідних параметрів енергетичного рельєфу. На ділянках 3 ¸ 5 встановлювалися значно менші порівняно з вихідними значеннями РВЕ. Можна припустити, що при грубому шліфуванні енергетичний рельєф поверхні швидко відновлюється, а при тонкому шліфуванні (поліруванні) створюється новий енергетичний стан поверхні. Послідовне шліфування металевої поверхні наждаковими шкурками різної зернистості приводить до циклічних змін в енергетичному розподілі РВЕ на поверхні. Зміни РВЕ при поверхневій обробці визначаються як величиною деформації, так і параметрами атомарній шорсткості. Підвищена густина дефектів у поверхневому шарі деформованих металів приводить до зниження рівня Фермі. В результаті вирівнювання хімічного потенціалу у всьому об`єму металу до поверхні стікаються електрони, тому у приповерхневій області створюється надлишковий від`ємний заряд. Внаслідок нерівномірності процесу деформування відбувається відповідне утворення “острівців” від`ємного заряду. Розглянута взаємодія електронної і іонної підсистем дає можливість простежити кінетику розподілу деформаційних процесів на поверхні за зміною розподілу РВЕ. Спостерігається зменшення РВЕ на самій доріжці тертя для всіх трьох розглянутих матеріалів. Ширина доріжки тертя визначається шириною спадів на кривих розподілу РВЕ, а відстані між спадами РВЕ відповідають діаметру кільцевої доріжки тертя. Виміри залежності РВЕ від часу випробування на тертя показали, що на початку РВЕ значно зменшується, а з часом після приробки перестає змінюватися. Експериментальні дані дозволяють зробити висновок, що існує відповідність між зміною величини РВЕ і параметрами структури приповерхневого шару металу, що характеризують сталий для даних умов режим тертя. У даній роботі було також вивчено можливість експресної оцінки зносостійкості металів за розподілом РВЕ по поверхні. Зразки однакового хімічного складу зазнавали випробування на абразивне зношення і на тертя з наступним виміром розподілу РВЕ впоперек доріжки тертя. Виявлено, що більшому зношенню зразків відповідає більше зменшення РВЕ. Сплав, що містить (%) 2,0 C + 18,0 Cr + 2,0 B, показав найбільший опір абразивному зносу. Коефіцієнт кореляції між РВЕ і параметрами зносу дорівнював 0,92, що свідчить про високий ступінь відповідності між цими величинами. Використання методу виміру розподілу РВЕ впоперек доріжки тертя дає можливість проводити відносну оцінку схильності різних металів до абразивного зносу. Одним з ефективних методів дослідження механічних властивостей приповерхневих шарів металів є індентування. На наступному етапі роботи ставилася задача дослідити закономірності розподілу КРП при індентуванні, закономірності формування енергетичного рельєфу та еволюції цього рельєфу з часом. Для усіх відбитків сферичного індентора спостерігалася характерна деформаційна зона, що відповідає ділянці поверхні контакту, рис.12. Діаметри відбитків, виміряні оптичним методом, відповідають ширині кривих розподілу КРП на рівні половини висоти. Отже, зміна КРП пов’язана з пластичною деформацією поверхні зі фактичною площею контакту. Тому, останню можна більш точно визначити за поверхневим розподілом КРП. В усіх проведених експериментах максимальна величина КРП на поверхні контактної ділянці не перевищувала 1,15 В, у той же час в процесі пластичного деформування розтягуванням для алюмінію реєструється величина КРП до 1,25 В. Це означає, що густина дислокацій, що вийшли на поверхню, при деформуванні в умовах контактуючих поверхонь менша ніж на вільній поверхні. Комплексний підхід у вивченні фізичних властивостей приповерхневих шарів металів означає вимір енергетичних, силових і структурних параметрів матеріалу. Отримані методом кінетичного індентування значення активаційного об`єму зразків дозволили пояснити структурні зміни в результаті різних поверхневих зміцнюючих обробок, таблиця 1. Глибина впровадження індентора в матеріал поверхневого шару складала ~ 0,1 мм. Це означає, що досліджувався зміцнений обробкою приповерхневий шар. Стискуючі залишкові макронапруження в приповерхневому шарі зразків обумовлені збільшенням густини дислокацій та розвитком дислокаційної структури. Як наслідок цього спостерігається кореляція між величиною залишкових макронапружень і активаційним об`ємом. Зростанню стискуючих напружень відповідає зменшення величини активаційного об`єму. Показано, що контактні напруження з ростом деформації збільшуються, виходячи на плато, що відповідає границі плинності сплаву. Хід кривих дозволяє виявити особливості пружно-пластичної деформації матеріалу в залежності від обробки. На підставі отриманих даних, наприклад, можна рекомендувати віброамплітудне шліфування і полірування для збільшення опору контактним деформаціям. Таблиця 1 Деякі характеристики матеріалу приповерхневого шару зразків з сплаву титана ВТ3-1 після різних видів поверхневої обробки.
Примітка: A – віброамплітудне шліфування і полірування, 30 хв.; B – обробка сталевими кульками діаметром 1,9 мм в ультразвуковому полі, 3 хв; C – віброамплітудне зміцнення керамічними гранулами діаметром 1,9 мм. Розділ
6. Зміни приповерхневої структури металів під впливом електроімпульсної та
магнітно-абразивної обробок. У даному розділі дисертації описано результати
досліджень впливу потужних імпульсів електричного струму і магнітно-абразивної
обробки на механічні властивості поверхневого шару металів. Через зразки
пропускався розряд конденсаторної батареї ємністю 200 мкФ. Тривалість розряду
складала 50 мкс. Максимальна зареєстрована термопарою температура знаходилася в
інтервалі 350¸520 0К. Після
електроімпульсної обробки (ЕІО) зразки випробовувалися на втому, а також
досліджувалися з використанням рентгеноструктурного аналізу. Визначалися такі
величини: макроскопічні залишкові поверхневі напруження σ; мікроскопічні
деформації Таблиця 2 Довговічність, залишкові напруження і параметри мікроструктури до і після ЕІО сплаву марки ВТ3-1. t – час попереднього зміцнення (УЗО).
Проходження електричних імпульсів через метал супроводжується відділенням теплової енергії. Оскільки будь-які дефектні області кристалу мають більш високий опір електричному струму, теплова енергія в основному виділяється в цих областях. Ця додаткова енергія сприяє переходу дефектних зон у рівноважний стан. Таким чином, дія імпульсів електричного струму специфічна локалізацією виділення теплової енергії. Автором запропонована і розглянута фізична модель еволюції пари точкових дефектів у зоні локального розігріву кристалу. Загальна енергія системи атомів представлена у вигляді:
де VR(rij) – потенціал парної взаємодії атомів і та j, відстань між якими rij; f(ni) – функція “занурення” атома i в електронну підсистему густиною ni. Підсумовування проводиться за всіма парами атомів моделі і по всіма атомами i. Використовувалися рівняння багаточасткового неадитивного потенціалу з числовими значеннями параметрів для кристала нікелю, записані у вигляді полінома для кожної пари взаємодіючих атомів. Рівняння враховує найближче оточення шляхом підсумовування поліноміальних функцій. Розглядалася кінетика взаємодії пари вакансія – міжвузловий атом. Моделювання на ЕОМ теплового імпульсу, створюваного електричним струмом, полягало в додаванні всім атомам, що оточують дану пару точкових дефектів ґратки, швидкостей за розподілом Гауса для трьох випадків миттєвих максимальних температур у термічному піку: 2000, 1500 і 1000 0К. Після виникнення температурного піка кристал релаксував протягом 12 пс. При цьому спостерігалися інтенсивні переміщення атомів поблизу області дефектів. При температурі 1000 0К, наприклад, число атомних переміщень у напрямку, перпендикулярному поверхні, складає 94 % від загального числа переміщень. Встановлено значну роль полів пружних напружень дефектів ґратки при їхній рекомбінації. Показано, що термічний пік навіть із відносно не дуже високою максимальною температурою здатний “заліковувати” області кристала з дефектами типу вакансія - міжвузловий атом. Виходячи з того, що механічні властивості поверхневого шару визначаються взаємозв'язком параметрів мікрогеометрії і напружено-деформованного стану матеріалу приповерхневого шару, в роботі вирішувалась задача дослідження закономірностей формування залишкових напружень поблизу поверхні при магніто - абразивної обробці. На рівні винаходу в даній роботі вперше встановлено, що магнітно-абразивна обробка металів і сплавів у робочому середовищі, що складається із суміші магнітно - абразивного порошку і феромагнітних тіл, є ефективним новим методом одночасного полірування і підвищення міцності сплавів (приблизно в 1,5 рази). Висновки 1. Вперше систематично виміряні розподіл роботи виходу електрона по поверхні алюмінію і сталей у процесі розтягування з постійною швидкістю. Отримано нові експериментальні підтвердження того, що в пружній області спостерігається зростання РВЕ, а в пластичній відбувається падіння РВЕ. Експериментально встановлено, що зменшення РВЕ визначається ступенем пластичного деформування і з його зростанням зміна РВЕ досягає граничного значення і насичення, після якого настає руйнування. Показано що, залежність РВЕ від ступеня деформації може бути описана аналогічно аналітичній залежності РВЕ від концентрації атомів, що адсорбуються на поверхні. Отримані при цьому значення густини ліній ковзання дислокацій, що вийшли на поверхню, добре узгоджуються з даними електронної мікроскопії. 2. Запропоновано фізичну модель, яка дозволяє кількісно оцінити РВЕ для деформованих металів. Вперше розроблено розрахункову схему, яка враховує наступні поправки до моделі “желе”: дискретність розподілу позитивного заряду; вплив релаксації іонних площин поблизу поверхні кристала на електронний розподіл; вплив діелектричного середовища, що граничить з поверхнею металу. Дані проведених розрахунків задовільно узгоджуються з експериментом. 3. Вперше розроблено модель розрахунку РВЕ для неідеальної поверхні металів в умовах їх пружного і пластичного деформування. Модель побудована на основі уявлень про взаємозв'язок РВЕ і електровід¢ємності атомів з урахуванням формування нанодефектів на поверхні. Обчислення, проведені для алюмінію і міді, показали задовільну збіжність з експериментальними даними. 4. Вивчено залежності РВЕ від розвитку фізичних процесів втоми алюмінію, жароміцних сталей і сплавів на основі титана. Проведені виміри значень РВЕ в осьових напрямках зразків, що зазнавали знакозмінних напружень. Вперше отримано, що на початкових стадіях випробувань РВЕ осцилює поблизу деякого значення, що свідчить про зворотність на цих стадіях процесів накопичення ушкоджень втоми і про зміну процесів зміцнення і релаксації, тобто процесів накопичення і анігіляції дефектів кристалічної структури. На наступній стадії впливу прикладених знакозмінних механічних напружень відбувається незворотне накопичення дефектів, розвиток процесів порушення неперервності кристалічної структури і руйнування. Встановлено, що в результаті структурних змін, які поступово підготовлюють зародження тріщин втоми, РВЕ зменшується. У зоні появи майбутньої тріщини криві розподілу РВЕ по поверхні мають характерний “деформаційний” провал. 5. На основі встановленого фізичного механізму явищ запропоновано кількісну модель кінетики структурних перетворень на поверхні металів у процесі втоми, яка включає рух деформаційних дислокацій по площинах ковзання, вихід дислокацій на поверхню і появу атомних заряджених сходинок, що і є причиною зниження РВЕ. З використанням розробленої моделі і виведених рівнянь виконані кількісні оцінки параметрів структурних та енергетичних змін на поверхні металів. 6. Вивчено вплив проміжної термічної обробки на міцність втоми досліджуваних сталей. Знайдено, що проведення відновлювального відпуску після випробувань, які складають 20 - 30 % середньої довговічності, є перспективним способом, що дозволяє істотно збільшити опір втоми. Вакуумна термообробка приводить до зменшення значень РВЕ на поверхні зразка в середньому на 100...120 мэВ. Відпуск зразків, проведений після механічної обробки (виготовлення), викликає різке збільшення величини РВЕ і істотне зменшення розкиду її значень. 7. Методом дифракційної електронної мікроскопії знайдено, що під дією циклічного навантаження спостерігається фрагментація мартенситних пластин у структурі високолегованих сталей, взаємодія дислокацій, їх часткова анігіляція і утворення субзернистої структури. Більшій втомній міцності сталей відповідає відносно однорідна дрібна субструктура. 8. Експериментально встановлено і доведено, що контактна деформація індентуванням і процес тертя супроводжуються зменшенням РВЕ в зоні відбитка від індентора і на доріжці тертя. Виявлено, що РВЕ чутлива до стану і типу структури поверхневого шару і може використовуватися при вивченні явищ контактної взаємодії металів. Послідовне шліфування металевої поверхні наждаковими шкурками різної зернистості приводить до циклічних змін в енергетичному розподілі РВЕ по поверхні. Для усіх видів шліфувань спостерігається граничне значення РВЕ. Із зменшенням параметра шорсткості РВЕ зростає. Величина градієнта РВЕ по поверхні залежить від ступеня локальної залишкової деформації. З часом енергетичний рельєф релаксує. Виявлено вплив окисного процесу при деформуванні металевих поверхонь; із збільшенням товщини окисних плівок спостерігається ріст РВЕ. Потенційний рельєф поверхні обумовлений нерівномірністю розподілу залишкових напружень в матеріалі, а також товщиною і складом поверхневих плівок. 9. Розроблено новий метод, що полягає у швидкій оцінці відносної зносостійкості металів на основі проведення економічних, екологічно чистих і простих по виконанню випробувань на тертя з наступним виміром розподілу РВЕ вздовж доріжок тертя. Розподіл РВЕ по поверхні безпосередньо пов'язаний з розподілом поверхневої енергії. Вимірювання РВЕ може бути використане для дослідження фізичних закономірностей опору металів тертю і зносу. 10. Встановлено, що електроімпульсна обробка приводить до збільшення довговічності металів при випробуваннях на багатоциклову втому. Вплив обробки імпульсним струмом проявляється у зниженні рівня залишкових макронапружень у приповерхневому шарі, зменшенні блоків мозаїки і росту мікронапружень. Вплив імпульсної обробки на структуру проявляється значної мірою для більш розвинутої дефектної структури. 11. У рамках молекулярно-динамічного моделювання показано, що термічний пік навіть з не дуже високою максимальною температурою (~1000 0К) здатний “заліковувати” області кристала з дефектами типу вакансія - міжвузловий атом. Термічні коливання атомів активують процес рекомбінації дефектів, в той час як направлено-орієнтуючий вплив здійснюється пружним полем, обумовленим дефектами. Імовірність переміщення міжвузлових атомів у напрямку до вакансій при рекомбінації відповідних дефектів у значній мірі визначається пружними полями і тому слабко змінюється з ростом температури. Зменшення кількості дефектів може досягатися короткочасними (~10-12–10-11 с) просторово локальними (порядку нанорозмірних) тепловими впливами (піками) з максимальною миттєвою температурою ~1000 0К і випадковим розподілом напрямків швидкостей атомів у тепловому піку. При цьому навколишні області атомних структур залишаються неушкодженими, тоді як при максимальних миттєвих температурах ~2000 0К спостерігається утворення нових дефектів, особливо поблизу вільної поверхні модельного кристала. 12. Розроблено оригінальні експериментальні установки для випробувань на одновісне розтягування, втому, кінетичне індентування, для випробувань на тертя і знос. Здійснені пристрої, що призначені для зміцнення поверхні металевих тіл з використанням електроімпульсного впливу і магнітно-абразивної обробки. Удосконалено методику виміру КРП, на основі аналізу залежності контактної різниці потенціалів від напруги компенсації з використанням одночасно комп'ютерної обробки результатів вимірів. Література 1. Лоскутов С.В., Левитин В.В., Серпецкий Б.А. О влиянии поверхностных органических плёнок на результаты рентгенодифрактометрического анализа напряжений в металлах // Нові матеріали і технології в металургії та машинобудуванні.– 1997.– № 1–2.– С.72 – 74. 2. Левитин В. В., Лоскутов С. В., Серпецкий Б. А. Исследование замковых соединений лопаток и дисков газотурбинных двигателей с применением резистометрии // Нові матеріали і технології в металургії та машинобудуванні.- 1997.- № 1-2.- С.70 -72. 3. Лоскутов С. В., Левитин В. В. О кинетике энергетического состояния металлической поверхности в процессе усталостного деформирования // Новые конструкционные стали и сплавы и методы их обработки для повышения надёжности и долговечности. - Сб. научн. тр. ЗГТУ. - Запорожье, 1998.- С. 37 - 38. 4. Серпецкий Б. А., Лоскутов С. В., Левитин В. В., Манько В. К. Повышение точности и производительности рентгенодифрактометрических измерений макроскопических напряжений // Заводская лаборатория. Диагностика материалов. Физические методы исследования и контроля. – 1998. – 3. – С. 28 –30. 5. Лоскутов С. В. Влияние пластической деформации на работу выхода электронов в алюминии // Физика металлов и металловедение. – 1998.– 86, № 2.– С. 61 – 66. 6. Лоскутов С. В. Закономерности распределения работы выхода электрона по деформированной поверхности металла // Известия вузов. Физика. – 1998. – 6.– С. 59 – 63. 7. Лоскутов С. В., Левитин В. В., Серпецкий Б. А. О физическом механизме развития. |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


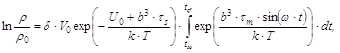 (8)
(8)