|
Дипломная работа: Механизмы имплантации в металлы и сплавы ионов азота с энергией 1-10 кэВДипломная работа: Механизмы имплантации в металлы и сплавы ионов азота с энергией 1-10 кэВМЕХАНИЗМЫ ИМПЛАНТАЦИИ В МЕТАЛЛЫ И СПЛАВЫ ИОНОВ АЗОТА С ЭНЕРГИЕЙ 1-10 кэВ ОГЛАВЛЕНИЕВВЕДЕНИЕ 1. Сравнительный анализ методов поверхностного модифицирования 2. Физические основы процесса ионной имплантации газов в металлы и сплавы 2.1 Основные характеристики метода ионной имплантации 2.2 Механизмы взаимодействия имплантируемых ионов с мишенью 2.3 Модель для расчета пробегов ионов в материале подложки 2.3.1 Ядерное торможение иона в материале 2.3.2 Электронное торможение иона в материале 2.4 Распределение примеси и дефектов в материале подложки в зависимости от энергии ионов азота 2.5 Остаточные концентрационные напряжения 3. Методики расчёта основных параметров физических процессов, происходящих при ионной имплантации 3.1 Методика расчета пробегов ионов методом Монте-Карло 3.2 Методика расчета распределения концентрации внедренных ионов по глубине материала 3.3 Методика расчёта остаточных концентрационных напряжений 4. Результаты расчёта параметров процессов взаимодействия имплантируемых ионов с материалом подложки 5. Экспериментальное оборудование 5.1 Установка для ионной имплантации азота в инструментальные материалы 5.2 Устройство системы электропитания имплантационной установки 5.3 Устройство датчика ионного тока Заключение Список Литературы ПРИЛОЖЕНИЯ ВВЕДЕНИЕ Развитие машиностроения во многом определяется решением проблемы надежности подвижных сопряжении машин на основе подбора высокоэффективных материалов и методов их технологической обработки, выбора смазочных материалов, покрытий и т.д. При этом основная тенденция заключается в стремлении к повышению реализуемых скоростей, давлений, рабочих температур при одновременном росте надежности. Это невозможно без использования деталей, имеющих высокие физико-механические характеристики поверхностных слоев, так как в абсолютном большинстве случаев именно они ответственны за коррозионную и радиационную стойкость, износостойкость и другие эксплуатационные характеристики изделий. Детали и механизмы машин во многих случаях работают при высоких тепловых и механических нагрузках, в химически активных и абразивных средах. Поэтому необходимы высококачественные методы поверхностного модифицирования изделий, которые должны иметь следующие характеристики [1 – 4]: · экологическая безопасность; · минимальное изменение геометрических размеров изделия; · отсутствие коробления; · внедрение строго дозированных количеств легирующей примеси; · максимальный диапазон концентраций легирующей примеси; · чистые условия проведения процесса, исключающие загрязнение образцов нежелательными примесями; · простота управления процессом; · высокая воспроизводимость получаемых структур; · экономичность метода. Для повышения эксплуатационных свойств материалов широко используются механические, термические, деформационно-термические и химико-термические методы упрочняющей обработки и легирования [5, 6, 9]. При использовании этих методов обработки материалов не всегда обеспечивается достаточно хорошая адгезия покрытий и упрочнение происходит не только на поверхности, но и в объёме изделия. В то же время для защиты деталей от изнашивания и коррозии достаточно поверхностного упрочнения материала. Основной же объем материала испытывает лишь сравнительно незначительные разрушающие воздействия нагрузок и химически активных сред и не требует упрочнения [3]. Ужесточение требований к структуре [7] и свойствам поверхностных слоев стимулировало развитие методов ионно-лучевой обработки [2, 18, 21], применение которых оказывается более целесообразным и экономически выгодным по сравнению с традиционными технологиями. На сегодняшний день, одним из перспективных методов ионно-лучевой обработки является ионная имплантация [1, 2, 12] – внедрение ускоренных ионов в твердые тела. Ионная имплантация приобрела в последнее время большое значение не только как способ создания микроэлектронных устройств, но и как мощный универсальный метод упрочняющей обработки. Материалы, попадая в условия облучения высокоэнергетическими ионами, претерпевают значительные структурные превращения, которые обуславливают резкое изменение их свойств. Анализ литературы [1 – 3, 10 – 15] показывает, что использование газов в качестве обрабатывающего вещества, позволяет значительно воздействовать на эксплуатационные характеристики деталей, однако вопрос этот в полной мере не изучен [3]. Сравнение методов упрочняющей обработки помогает выявить основные преимущества метода ионной имплантации. 1. Сравнительный анализ методов поверхностного модифицирования Основные виды традиционной термической обработки - отжиг, закалка, отпуск и старение – приводят к изменению не только поверхностных, но и объёмных свойств материалов. В то же время для защиты деталей от износа и коррозии на практике в ряде случаев необходимо и дополнительное поверхностное упрочнение материала [3]. Каждый из используемых с этой целью методов поверхностного модифицирования имеет свои преимущества, недостатки и ограничения. Поэтому на практике конкретный метод изменения поверхностных свойств выбирают, исходя из требований к характеристикам поверхностного слоя и экономичности. Наиболее распространенными группами методов поверхностного модифицирования являются: - поверхностного пластического деформирования; - химико-термической обработки; - ионной имплантации. Повышение долговечности деталей машин методом поверхностного пластического деформирования [5, 6] широко используется для повышения сопротивляемости малоцикловой и многоцикловой усталости деталей. Поверхностное деформирование повышает плотность дислокации в упрочненном слое, измельчает субструктуру (величину блоков), а при обработке закаленных поверхностей уменьшает количество остаточного аустенита [16]. Существенным недостатком данного метода является высокая шероховатость поверхностей после обработки. Химико-термическая обработка (ХТО) [18] заключается в сочетании термического и химического воздействий на металлы и сплавы для изменения химического состава структуры и свойств в поверхностных слоях. ХТО сводится к диффузионному насыщению поверхностного слоя стали неметаллами (С, N, Si и др.) или металлами (Сr, Аl и др.) в процессе выдержки при определенной температуре в активной среде: твёрдой, жидкой или газовой (плазма) [18, 19]. ХТО использует оба способа воздействия на образец одновременно в одном процессе — изменение структуры и химического состава поверхностного слоя. Таким комбинированным воздействием можно получить взаимоисключающие свойства образца, например, высокую твердость и вязкость одновременно. При этом высокая твердость или износостойкость присуща лишь тонкому поверхностному слою, в котором диффузионным способом был изменен химический состав, а вязкость детали обеспечивается свойствами сердцевины, которая создается химическим составом выбранной стали и способом ее термической обработки. Преимущество ХТО перед механическими, термическими и деформационно-термическими методами упрочняющей обработки, заключается в том, что происходит термическое упрочнение сердцевины и поверхностного слоя образца. Характерной особенностью ХТО является необходимость нагрева заготовок, что связано с большими затратами энергии [3, 5, 6]. Основой всех процессов ХТО является диффузия, которая определяет длительное время обработки образцов. ХТО не позволяет получить концентрацию примесей выше предела растворимости диффундирующего элемента в обрабатываемом материале при температуре процесса [19]. Недостаточно интенсивное удаление продуктов реакции от поверхности или загрязнение поверхности окислами, пригарами, сажей и т.д. увеличивает сопротивление диффузионным процессам [20]. Поэтому перед ХТО необходимо подвергать образцы тщательной очистке [3, 7]. Все эти факторы, а также громоздкость оборудования приводят к существенным затратам. Чем больше зона химического соединения, тем больше изменение размера образцов; кроме того, в процессе обработки возможно коробление образцов, что нежелательно [17, 19]. ХТО часто связана с применением вредных для здоровья веществ, что вызывает необходимость дополнительных расходов на обеспечение экологической безопасности [3]. Ионные технологии поверхностного модифицирования являются на сегодняшний день наиболее прогрессивными [21, 25, 28, 30, 31]. Однако, ионные технологии требуют применения вакуумной техники и высоких ускоряющих напряжений. Очевидные преимущества этой группы методов включают легкость управления пучком заряженных частиц, возможность разгонять их до практически любой необходимой энергии и легко изменять вид используемых ионов, исключительную чистоту методов, воспроизводимость и контролируемость параметров обработки [21, 25, 31]. Используемые ионные технологии предназначены: 1) для создания покрытий различного функционального назначения, в том числе износостойких; 2) для поверхностного модифицирования за счет внедрения ионов в материал подложки без формирования покрытий. В первом случае, при наиболее распространенном на практике ионно-плазменном напылении [23, 28, 29, 32], осаждение потока ионов ведется из плазмы на деталь, находящуюся под отрицательным потенциалом, значение которого достигает 103 В и выше. Между образцом и заземленными частями установки создается тлеющий разряд в инертном газе, обычно аргоне, находящемся под давлением в единицы Паскалей. Разряд обеспечивает очистку поверхности за счет распыления адсорбированных газов. После очистки материала подложки ионами аргона, производится ионная бомбардировка поверхности образцов ионами металла с целью внедрения ионов в поверхностный слой, создания переходной зоны между покрытием и основным материалом для повышения адгезии. Бомбардировка сопровождается нагревом поверхности образцов до температуры, которая не должна превышать температуру отпуска материала подложки. Метод позволяет получать пленки равномерной толщины и мелкодисперсной структуры с хорошей адгезией к подложке [31]. На практике получили широкое распространение покрытия из чистых металлов, нитридов и карбидов титана, циркония, хрома [27] и др. К недостаткам ионно-плазменного напыления можно отнести большое число параметров, активно влияющих на структуру и свойства получаемых покрытий, а также возможные перегрев поверхности выше температуры отпуска и разупрочнение сталей или, наоборот, недостаточный нагрев поверхности, приводящий к низкой адгезионной прочности покрытия [30]. Ионные методы формирования покрытий имеют общее свойство — результатом их применения является изменение размеров обрабатываемого изделия [3, 8, 10, 11]. Применение этих методов связано с необходимостью обеспечения высокой адгезии покрытия к материалу основы, для чего требуется поддержание определенного температурного диапазона осаждения [3, 33]. В связи с вышеизложенным, наиболее перспективным является другое направления развития ионных технологий, - поверхностного модифицирования за счет внедрения ионов газов в материал подложки без формирования покрытий, одна из разновидностей так называемой ионной имплантации [21, 33]. Суть метода заключается в поверхностной обработке изделия ионами с энергией, достаточной для их внедрения в поверхностные слои материала. Пороговая энергия, выше которой начинается внедрение ионов составляет примерно 3*10-18 Дж (рисунок 1.1). Глубина проникновения при энергии частиц 10-18 – 10-17 Дж не превышает нескольких межатомных расстояний (до 10 Å). Обычно рассматривают три энергетических диапазона ионной имплантации: низкоэнергетическая (10-17 10-16 Дж), имплантация ионов средних энергий (10-15 10-14 Дж), высокоэнергетическая имплантация (10-13 Дж и выше) [21, 22].
Рисунок 1.1 – Энергетические диапазоны воздействий ионного потока на поверхность твёрдого тела. Ряд исследователей отметили [3, 21, 24, 26] в качестве результата ионной имплантации значительное повышение эксплуатационных характеристик изделий, таких как механические свойства, износостойкость, коррозионная стойкость, циклическая прочность и т.д. К преимуществам метода ионной имплантации следует отнести: · возможность получения практически любой комбинации матрица – легирующий элемент или легирующие элементы; · возможность проведения процесса комнатной температуре; · внедрение строго дозированных количеств легирующих примесей; · отсутствие зависимости предельной концентрации вводимой примеси от предела растворимости в материале подложки; · чистые условия проведения процесса, исключающие загрязнение образцов нежелательными примесями; · простота управления ионным пучком и возможность обработки локальных участков поверхности; · практически неизменность размеров обрабатываемой детали; · отсутствие коробления деталей, даже малой жёсткости; · высокая воспроизводимость получаемых структур; · обеспечение экономного легирования. Недостатком реализации метода ионной имплантации является сложность и громоздкость оборудования и отсутствие его серийного производства. Таким образом, из выше рассмотренных групп методов в силу неоспоримых преимуществ можно выделить методы поверхностного модифицирования за счет внедрения ионов в материал подложки без формирования покрытий – ионную имплантацию газов в поверхности металлов и сплавов. 2. Физические основы процесса ионной имплантации газов в металлы и сплавы 2.1 Основные характеристики метода ионной имплантацииОсновными параметрами ионной имплантации являются: - энергия имплантируемых ионов, Дж; - доза облучения, м-2; - время облучения, с. Физические процессы при имплантации
ионов газов с энергией в диапазоне 1 – 10 кэВ ( Таким образом, осуществление ионной
имплантации в диапазоне 1 – 10 кэВ ( Технологические возможности ионной имплантации определяются верхним пределом концентрации имплантированных атомов и толщиной слоя, характеризующегося новыми свойствами. В процессе имплантации при торможении бомбардирующего иона в поверхностном слое материала создаются каскады смещенных атомов, при этом поверхностные атомы, получившие энергию, достаточную для преодоления сил поверхностной связи, выбиваются наружу и происходит распыление облучаемого материала. Вместе с атомами обрабатываемого материала происходит выбивание и атомов имплантируемой примеси. Вследствие этого процесс распыления накладывает ограничение на количество имплантируемых в материал атомов, что ведет к насыщению общей концентрации имплантированной примеси. В разделе 2.4 приведена расчётная зависимость для определения максимальной концентрации вводимой примеси. Как показывают оценки и эксперименты, обусловленный распылением поверхности в процессе имплантации верхний предел имплантированной примеси ограничен 20...50 атомными %, что является вполне достаточным для получения сплавов и управления свойствами поверхности. Реально это соответствует диапазону доз 1021... 1022 м-2 [21]. На практике доза облучения, как правило, колеблется от 1019 до 1022 м-2 [8, 21, 25]. При дозах меньше 1019 м-2 повышение эксплуатационных характеристик изделий незначительно [25]. При увеличении дозы имплантации выше 1022 м-2 улучшение эксплуатационных характеристик изделий существенно замедляется, и начинают проявляться различные нежелательные эффекты, например, радиационное распухание [20, 41], которые приводят к разрушению поверхностного слоя обрабатываемого материала. Наиболее просто процесс ионной имплантации газов в металлы и сплавы может быть реализован с использованием схемы, приведенной на рисунке 2.1. В результате термоэлектронной эмиссии вольфрамовой проволоки 1 создаётся поток электронов, который проходит через промежуточный анод 2 и фокусируется при прохождении анодной вставки 3. Магнитное поле, создаваемое соленоидом 4, также обеспечивает фокусировку потока электронов. Сталкиваясь с атомами поступающего в камеру 5 газа (азота), электроны ионизируют его.
Рисунок 2.1 – Схема ионной имплантации газов в поверхностные слои металлов и сплавов в вакуумной камере. 1 – катод; 2 – промежуточный анод; 3 анодная вставка; 4 – соленоид; 5 – камера, в которую подаётся газ; 6 – анод; 7 экстрактор; 8 – фокусирующий электрод; 9 – подложка (легируемый материал); 10 ионный пучок. Ионы газа вытягиваются и ускоряются под действием приложенного между экстрактором 7 и анодом 6 высокого напряжения (10 – 50 кВ). Ионный поток 10 фокусируется, проходя через фокусирующий электрод 8, и попадает на поверхность образца 9. При прохождении через отверстие в экстракторе ионы обладают энергией, достаточной для внедрения в поверхностные слои образца. 2.2 Механизмы взаимодействия имплантируемых ионов с мишеньюИз литературных источников [8, 21,
26, 36, 37, 48, 49], известно, что механические свойства обрабатываемой поверхности
после имплантации ионов зависят, прежде всего, от концентрации внедренных ионов
и образующихся в процессе имплантации радиационных дефектов. Для расчета
пробегов и концентраций ионов при имплантации применяется теория
Линхардта-Шарфа-Шиотта (ЛШШ), изложенная в работах [21, 22, 46 – 48].
Существенное влияние на распределение примеси по глубине поверхностного слоя
изделия оказывает радиационно-стимулированная диффузия. На диффузионные
процессы существенное влияние оказывает температура нагрева поверхностного слоя
образца. Однако в случае ионов газов с энергией в диапазоне 1 – 10 кэВ ( В настоящее время не существует теории, достаточно полно объясняющей модификацию поверхностных свойств материалов при ионной имплантации. При взаимодействии бомбардирующих ионов с твердым телом происходит ряд процессов, обуславливающих модификацию свойств материалов. Такими процессами являются внедрение ионов, которое сопровождается образованием радиационных дефектов и их последующая диффузия. Физические модели и методики расчетов характеристик указанных процессов приведены в работах [2, 3, 8, 13, 15, 21, 22, 28, 36, 48, 49]. Однако, в настоящее время не существует модели модификации поверхностного слоя реального материала, которая достаточно полно учитывала бы все вышеназванные механизмы, происходящие при ионной имплантации [3].
Рисунок 2.2 – Схема процессов, происходящих при ионной имплантации За основу при описании модификации поверхностного слоя реального материала возьмем схему процессов, происходящих при ионной имплантации, приведенную на рисунке 2.2. Она наиболее полно учитывает процессы взаимодействия ионов с веществом (рисунок 2.2): внедрение ионов, которое сопровождается образованием радиационных дефектов, дефектообразованием, нагревом поверхности материала и их последующая диффузия. На схеме отражены входные и выходные характеристики данных процессов: полная доза имплантации Ф, распределение примеси по глубине Ci(z), температурное поле Q(z,t), распределение элементарных радиационных дефектов Cv(z), распределение примеси Ci(z,t) и дефектов Cv(z,t), обусловленное радиационно-стимулированной диффузией и поле остаточных концентрационных напряжений s(z). В разрабатываемой модели не отражен эффект дальнодействия (формирование развитой дислокационной структуры на глубинах, значительно превышающих глубину проникновения примеси при имплантации), обнаруженный рядом автором [2, 21, 44]. Несомненно, что этот эффект оказывает существенное влияние на свойства обработанного материала. Существующие гипотезы [21, 45, 53, 55] не позволяют количественно оценить этот эффект. Исследователи предполагают, что плотность образующейся в результате эффекта дальнодействия дислокационной структуры определяется как характеристиками ионного потока, так и элементным составом материала подложки [3]. Важной задачей является оценка свойств обработанного материала в зависимости от первоначальной концентрации примеси и образованных в процессе имплантации радиационных дефектов. Как показано в [3, 15, 49, 52, 54] остаточные концентрационные напряжения определяют свойства материала после имплантации. Анализ существующей литературы показал, что для прогнозирования структуры и свойств поверхностного слоя образцов после имплантации при известных параметрах ионного потока (управляемых за счет изменения тока на катоде, ускоряющего напряжения между анодом и экстрактором (рисунок 2.1), давления газа в камере и др.), необходимо знание параметров: 1) дозы имплантации; 2) пробегов ионов при известном ускоряющем напряжении; 3) распределения примеси в материале после имплантации; 4) полей остаточных концентрационных напряжений. Для их нахождения необходимо решить задачи выбора и усовершенствования методик расчета соответствующих параметров. В связи с этим целью дипломной работы является разработка комплекса моделей, позволяющих на основе данных о технологических параметрах имплантации составить прогноз о свойствах материала подложки после имплантации: 1. Модель для расчета пробегов ионов азота в металлах и сплавах под действием энергии имплантации; 2. Модель распределения ионов азота в поверхностном слое материала подложки после имплантации; 3. Модель распределения дефектов в поверхностном слое материала подложки после имплантации; 4. Модель расчета остаточных концентрационных напряжений в поверхностном слое материала подложки после имплантации. 2.3. Модель для расчета пробегов ионов в материале подложкиДля металлов и сплавов распределение пробегов по глубине оказывается приблизительно гауссовым [3]. Имеются трудности при теоретическом описании в случае больших интегральных доз облучения, когда на форму профиля примеси по глубине существенно сказывается распыление поверхности мишени, а также рассеяние ионов на атомах внедренной примеси [3]. Наиболее точные результаты расчета энергетических потерь получаются при использовании теории ЛШШ, в основе которой лежит утверждение о том, что основными механизмами торможения частиц в обрабатываемом веществе являются неупругие соударения с электронами (электронное торможение) и упругие соударения с ядрами (ядерное торможение). В работе Линдхарда и др. [46, 47, 50, 51] получены уравнения, описывающие связь между энергией и пробегами ионов в аморфных мишенях. Многочисленные эксперименты демонстрируют достаточно хорошее согласие с теорией ЛШШ [1, 8, 11, 12, 22, 23, 56, 57]. Модель ЛШШ основана на следующих предположениях: 1) мишень считается аморфной, т. е. из рассмотрения исключаются случаи коррелированных последовательных столкновений; 2) в работе используется потенциал, рассчитанный на основе статистической модели атома Томаса—Ферми, с учётом только электростатического взаимодействия между электронами; 3) энергия, передаваемая атомам мишени в процессе столкновений, много меньше кинетической энергии иона; 4) основными механизмами торможения частиц в обрабатываемом веществе являются неупругие соударения с электронами (электронное торможение) и упругие соударения с ядрами (ядерное торможение). Оба механизма считаются независимыми в процессах торможения; 5) учитываются флуктуации энергии, обусловленные в процессе торможения только взаимодействием с ядрами; 6) при описании взаимодействия иона с атомами подложки используется классическое приближение бинарных столкновений. Каждое из этих предположений ограничивает область применимости теории. В частности, предположение 1 исключает случай кристаллических и очень тонких аморфных мишеней. В этой модели не учитывается также оболочечное строение атомов. При близких атомных массах и порядковых номерах сталкивающихся атомов неупругие и упругие процессы становятся коррелированными, поскольку таким столкновениям соответствует значительная ионизация в обеих атомных подсистемах. Ионизация, в свою очередь, изменяет форму потенциала взаимодействия, а, следовательно, и угол рассеяния частиц. Такого рода корреляции могут существенно влиять на форму распределений ионов по пробегам (моменты кривой распределения высоких порядков). Используемая в теории ЛШШ статистическая модель атома Томаса-Ферми, позволяет достигнуть наилучшего совпадения результатов расчетов с экспериментальными данными.
Рисунок 2.3 — Схема пробега иона в твёрдом теле. (1) – поток ионов; (2) – путь иона в материале; (3), (4), (5) – атомы в узлах кристаллической решётки материала подложки; (6) и (7) – начальное и конечное положение иона при внедрении в материал подложки. Ионная имплантация (рисунок 2.3) охватывает два взаимосвязанных процесса: внедрение (легирование) и радиационную обработку (дефектообразование) [31]. При бомбардировке твердых тел тяжелыми заряженными частицами (массой более 1 а.е.м.) возникают эффекты, которые способствуют их торможению или рассеянию. Эти эффекты классифицируют следующим образом [2, 21, 22]: · Неупругие соударения со связанными электронами тормозящего вещества. Потеря энергии при таких соударениях обусловлена возбуждением атомов или молекул; · Неупругие соударения с ядрами. Они вызывают тормозное излучение, возбуждение ядра или ядерные реакции; · Упругие соударения со связанными электронами. · Упругие соударения с ядрами или атомами. При этом часть кинетической энергии передается атомам мишени. · Черенковское излучение. Оно возбуждается частицами, которые движутся в среде со скоростью, больше фазовой скорости света. При ионной имплантации частицы
движутся со скоростью меньше фазовой скорости света, поэтому черенковское
излучение отсутствует. При торможении частиц неупругие соударения с ядрами и
упругие столкновения с электронами не играют большой роли по сравнению с
неупругими соударениями с электронами (электронное торможение) и упругими
соударениями с ядрами (ядерное торможение). Поэтому в дальнейшем целесообразно
рассматривать лишь эти два механизма. Какой из этих эффектов будет преобладать,
зависит от энергии и массы ускоренных частиц и массы и порядкового номера
атомов вещества. В диапазоне энергий, важных для ионной имплантации (от 1 кэВ ( Для расчета торможения первичных ионов в веществе введено понятие сечения электронного и ядерного торможения Se,n [22, 31]:
где Полный пробег частицы определяется из соотношения [21]:
где R - средняя общая длина пути иона в материале подложки, м, при его начальной энергии Е0, Дж. Наибольший практический интерес представляет проекция пробега иона на направление имплантации Rp, которая определяет наиболее вероятную ее глубину [3]:
где M1 — масса имплантируемого иона, кг. Эта формула справедлива в довольно широком интервале масс ион-атом, поэтому именно её и следует использовать при расчётах. Формула (2.3) позволяет рассчитать средний проецированный пробег для одноатомных мишеней [22]. Для расчёта пробега в мишенях сложного химического состава, каковыми являются сплавы, можно воспользоваться статистическими методами имитационного моделирования, в частности, методом Монте-Карло [20]. В разделах 2.3.1 и 2.3.2 приведены расчётные формулы для ядерных и электронных потерь энергии ионом в веществе [22, 57]. Величина вклада ядерных и электронных потерь энергии в общие потери энергии ионом различна для разных энергетических диапазонов (рисунок 2.4). Из анализа графика на рисунке 2.4 следует, что при низких энергиях
ионов (
Рисунок 2.4 – Общий вид зависимости тормозных сечений электронного и ядерного торможения от энергии иона. Потери энергии определяются в основном электронным торможением, если энергия налетающих частиц превышает Eкр:
где Таким образом, из анализа графика на
рисунке 2.4 и из условия
(2.4) следует, что в диапазоне
энергий 1 – 10 кэВ ( 2.3.1 Ядерное торможение иона в материалеЕсли проинтегрировать энергию, передаваемую ионом атому мишени при столкновении Tn по всем возможным потерям энергии при столкновении, то получим упругие потери энергии на единицу длины пути [1, 2, 12, 21, 22, 57]:
где Tmax — максимально возможная энергия, передаваемая при лобовом столкновении, Дж; dσ — дифференциальное поперечное сечение взаимодействия, м2. Таким образом, для нахождения потерь энергии ионом при столкновении с атомами поверхностного слоя материала образца, необходимо знать энергию Tn, Tmax и сечение рассеяния dσ. Для нахождения вышеуказанных параметров рассмотрим процесс столкновений частиц на основе классической механики. Тогда с углом рассеяния сталкивающихся частиц можно связать прицельный параметр p и классическую траекторию в процессе столкновения. Уравнения, описывающие траектории взаимодействующих частиц, значительно упрощаются, если рассматривать движение в системе центра масс (СЦМ). Рисунок 2.5 иллюстрирует положение и угловые координаты частиц при максимальном их сближении в лабораторной системе координат (ЛСК). Одна из частиц (M1) до столкновения двигалась со скоростью v, а другая (M2) – покоилась. Углы отклонения частиц после столкновения в ЛСК q1 и q2 выражаются через угол j формулами [22]:
где α – угол отклонения иона в СЦМ при столкновении, рад. Абсолютные величины скоростей частиц
после столкновения
Рисунок 2.5 – Схема столкновения двух частиц в ЛСК.
Тогда упругие потери энергии Tn ионом при столкновении с атомом подложки в ЛСК рассчитываются согласно (2.7) по формуле:
где E – энергия иона до столкновения; параметр
Угол рассеяния α налетающей
заряженной частицы в центральном силовом поле c потенциальной энергией U(r)
наиболее удобно решать исходя из законов сохранения энергии
где r – радиус-вектор иона,
м; p - прицельный параметр, м (расстояние, на котором ион
прошёл бы от атома в отсутствие силового поля); Подставим величину
Отсюда
Преобразуем выражение (2.11) к виду:
тогда из (2.13) и (2.14) получим
и, следовательно,
Рисунок 2.6 – Траектория частицы в СЦМ.
На рисунке 2.6 показана траектория движения иона в системе центра масс. Эта траектория симметрична по отношению к прямой, проведенной в ближайшую к центру точку орбиты (см. на рисунке 2.6 прямая ОА). Углы между ОА и обеими асимптотами к траектории одинаковы. Если обозначить эти углы χ0, то видно, что угол рассеяния иона в СЦМ равен:
Из (2.16) следует, что
Так как из (2.10) и (2.11)
То
где rmin — минимальное расстояние, на которое
частица приближается к рассеивающему центру, м; v — относительная скорость сталкивающихся частиц на "бесконечном"
расстоянии друг от друга, Таким образом, угол рассеяния иона α в СЦМ зависит от формы потенциальной энергии поля U(r) и кинетической энергии иона Eотн:
Величина rmin есть значение r при
Важнейшей характеристикой процесса рассеяния является эффективное сечение рассеяния:
где п — число частиц,
проходящих в единицу времени через единицу площади поперечного сечения
однородного пучка; dN — количество
частиц, рассеянных в единицу времени в единицу телесного угла Для ионов с энергией 1 – 10 кэВ (
и поэтому
Следовательно, окончательно имеем
Итак, зная потенциальную энергию взаимодействия сталкивающихся частиц U(r), энергию Tn, Tmax, α и сечение рассеяния dσ по формулам (2.8), (2.9), (2.20) и (2.26) можно найти упругие потери энергии ионом и дифференциальное сечение рассеяния. Главную роль играет выбор потенциала взаимодействия. Если скорость налетающей частицы сравнима со скоростью любого электрона атома мишени или меньше ее, то необходимо учитывать экранирование ядер атомными электронами. В настоящее время еще не найдено точное значение потенциала взаимодействия частиц с учетом экранирования ядер электронами [1, 2, 12, 21, 22, 57]. Однако существует несколько приближенных выражений для потенциала, хорошо описывающих взаимодействие частиц в различных энергетических интервалах [22, 57 – 61]. Потенциал Томаса-Ферми-Фирсова [67 – 69]. При изучении систем со многими взаимодействующими частицами приходится ограничиваться приближенными методами, применение которых дает удовлетворительное описание реальных свойств и параметров. Для атомов и молекул такими методами являются: вариационный метод и метод самосогласованного поля Хартри—Фока [65, 70]. Вариационный метод обычно используется только для легких атомов, в то время как методом Хартри—Фока могут быть изучены любые атомные системы. В методе самосогласованного поля каждый электрон рассматривается движущимся в сглаженном симметричном относительно центра (ядра) потенциальном поле, образованном ядром и всеми электронами. Состояние отдельного электрона атома может быть описано некоторой собственной функцией, а собственная функция всего атома комбинируется из собственных функций отдельных электронов. Для атомной системы с большим числом электронов движение частиц под действием самосогласованного потенциала может считаться квазиклассическим в преобладающей части пространства. Потенциал в этом случае является слабоменяющейся функцией координат за исключением области вблизи ядра и периферийной части атома. Квазиклассическое приближение к уравнениям Хартри—Фока носит название приближения Томаса—Ферми [63, 71]. В статистической модели атома Томаса—Ферми объем атома разделяется на элементы объема dv, в которых содержится значительное число электронов и в каждом из них потенциал можно считать постоянным. Эти условия не выполняются в периферийной области атомов из-за малого количества электронов, а около ядра из-за резкого изменения потенциала. Для устранения этих недостатков квазиклассического приближения приходится вводить квантовые поправки. В статистической модели атома Томаса—Ферми принимается во внимание только электростатическое взаимодействие между электронами, тогда как взаимодействие электронов с параллельными (обменная поправка) и антипараллельными (корреляционная поправка) спинами не учитывается. Таким образом, из статистической теории атомных систем можно найти распределение потенциала или электронной плотности как функции расстояния от ядра r [22, 57]:
где Функция экранирования - Зоммерфельда [58]:
- Гаспара [59]:
- Тейтца [60]:
- Видефола [61]:
Литературные данные [46, 47, 57 – 61, 76, 78] не позволяют выбрать из этих аппроксимаций наилучшую, поэтому при практических расчетах можно использовать любую из предложенных функций. С повышением энергии ионов возрастает
вклад неупругого торможения на электронах материала подложки и при 2.3.2 Электронное торможение иона в материалеВ настоящее время еще не получена общая формула, описывающая неупругие потери энергии ионом во всем диапазоне энергий имплантации [3]. Поэтому приходится ограничиваться формулами, справедливыми для узких энергетических интервалов. Расчет электронных потерь энергии
можно проводить на основе теорий Фирсова [22] и Линдхарда – Шарфа [21]. Для
диапазона энергий имплантируемых ионов 1 – 10 кэВ ( Формула Линдхарда—Шарфа [47]. Авторы нашли формулу, позволяющую вычислить потери энергии на единицу длины пути:
где Формула (2.32) подходит для расчёта электронных потерь энергии ионом в одноатомных поликристаллических материалах. В формуле нет связи между потерями энергии и прицельным параметром, что увеличивает погрешность результатов. Поэтому для расчётов методом Монте-Карло целесообразнее использовать формулу Фирсова [74] или Кишиневского [75]. Формула Фирсова. В теории Фирсова учитывается непосредственная связь между потерей энергии и прицельным параметром, что позволяет построить более адекватную модель, основанную на вероятностных методах расчета. Средняя энергия Te передаваемая атому мишени при одном столкновении, равна:
Нахождение потерь энергии на единицу длины пути сопряжено со значительными вычислительными трудностями, так как при этом необходимо проводить усреднение по всем параметрам соударений. Однако формулу (2.33) можно использовать в методе Монте-Карло, так как в этом случае потери энергии ионом считаются для каждого отдельного взаимодействия ион-атом. Формула применяется для атомов с близкими Z, причем Z1 и Z2 должны быть больше 10. При ионной имплантации азота в металлы Z1 ¹ Z2 и Z1 = 7 (Z1 < 10), значит использование формулы (2.33) для расчёта электронных потерь энергии ионами азота при имплантации в металлы и сплавы может существенно увеличить погрешность результата. Обобщение формулы (2.33) на случай, когда Z1 ¹ Z2, получено Л. М. Кишиневским. Формула Кишиневского. Согласно его расчетам
где Zmin — меньший, a Zmax — больший из зарядов сталкивающихся частиц. Формула (2.34) позволяет получить более точные результаты, так как учитывает связь между потерями энергии и прицельным параметром и учитывает различие между Z1 и Z2. Она наиболее подходит для расчёта методом Монте-Карло электронных потерь энергии ионами азота при имплантации в металлы или сплавы. Рассчитав потери энергии по формулам (2.5) и (2.32) можно найти средний пробег и средний проецированный пробег ионов по формулам (2.2) и (2.3) в различных фазах сплавов или чистых металлах. Для расчёта потерь энергии ионами при имплантации в реальные материалы, имеющие сложный химический состав, необходимо воспользоваться соотношениями (2.8) и (2.34). Также, определив угол рассеяния α из формулы (2.21), можно по формуле (2.25) определить дифференциальное сечение рассеяния. Полученные из формул (2.2) и (2.3) значения пробегов ионов используются для расчёта распределения примеси в твёрдом теле после имплантации. 2.4 Распределение примеси и дефектов в материале подложки в зависимости от энергии ионов азотаВследствие статистического характера взаимодействия ионов с атомами мишени наблюдается разброс пробегов ионов. Для металлов и сплавов распределение пробегов ионов приблизительно гауссовское. Такое распределение характеризуется двумя параметрами — средним значением Rp и среднеквадратическим отклонением ΔRp (страгглингом пробега). Для определения распределения имплантированных атомов наряду с параметрами пробега Rp и ΔRp нужно знать полную дозу имплантированных ионов Ф, м-2. Её можно получить через полный заряд всех ионов Q, Кл, который можно измерить в процессе имплантации [22]. Удельная доза имплантируемых ионов:
где q — заряд иона, Кл; Q — полный заряд, Кл; А — площадь имплантации, м2. При использовании этой формулы предполагается, что все попавшие на мишень ионы являются ионами заданного вида примеси с зарядом q и остаются в имплантируемой мишени и что устройство измерения правильно интегрирует ток пучка, а легируемая площадь А корректно определена. Однако, приведенные выше предположения не всегда достижимы в существующих системах измерения дозы. Поэтому измерение дозы имплантации всегда проводится с той или иной погрешностью, которая обусловлена следующими факторами: неоднородностью приходящего на мишень ионного пучка по зарядовому и массовому составу, недостатками измерения цилиндром Фарадея и блоком измерения дозы. Основную погрешность в измерении дозы имплантации вносит нейтральная компонента пучка, которая появляется в результате перезарядки ионов в области после ускорения. Этот происходит при столкновении ионного потока с потоком выбитых ими электронов с поверхности материала подложки. Нейтральные атомы не только нарушают корреляцию между интегрируемым током и дозой, но для систем с электростатическим сканированием приводят к значительной неоднородности дозы имплантации. Одним из основных процессов, сопровождающих ионное облучение твёрдого тела является образование в нём нарушений кристаллической структуры из-за передачи энергии иона атомам и электронам вещества. Определяющую роль при образовании дефектов играют ядерные взаимодействия. Если энергия, передаваемая ионом атому решётки (упругие потери), превышает энергию связи атома в кристаллической решётке, то последний выбивается из своего положения и переходит в междоузлие. Таким образом возникает точечный дефект – вакансия-межузельный атом (пара Френкеля). Для железа и сплавов на его основе энергия связи составляет 40 эВ. Если энергия, переданная первично смещённому атому, превышает энергию связи в несколько раз и более, то атом, в свою очередь может сместить другие атомы, те – следующие и т.д. Так образовываются каскады смещений. Напряжения, возникающие при образовании вакансии являются растягивающими, а имплантированный азот создаёт напряжения сжатия, то есть противоположные по знаку. Таким образом, для расчёта остаточных концентрационных напряжений, кроме концентрации ионов, необходимо учитывать и концентрацию вакансий. Концентрация ионов Сi(х) как функция расстояния от поверхности выражается соотношением (2.36), а концентрация вакансий Сv(х) соотношением (2.37) [1 3, 12, 21, 57]:
где х — расстояние от
поверхности металла (глубина проникновения иона в материал), м; Как показано в работе [21] в режиме насыщения максимальная концентрация имплантированной примеси Nmax определяется выражением:
где N - плотность атомов обрабатываемого материала, м-3, S - коэффициент распыления. Коэффициент распыления равен числу атомов, выбиваемых одним падающим ионом и рассчитывается по формуле:
где as – безразмерный коэффициент, характеризующий эффективность передачи энергии, который зависит от отношения масс взаимодействующих частиц; Sn - сечение упругого торможения при начальной энергии иона E0, Дж; Eb – энергия связи атомов на поверхности обрабатываемого материала, Дж. Таким образом, теоретически величина предельной концентрации примеси не зависит от дозы облучения, определяясь плотностью атомов обрабатываемого материала и коэффициентом распыления его ионами имплантируемой примеси. Поскольку коэффициент распыления является функцией порядковых номеров и массовых чисел иона и обрабатываемого материала, а также энергии иона, то величина Nmax будет существенно зависеть от этих параметров. Поэтому изменяя энергию иона можно менять максимальную концентрацию имплантированной примеси. Также и для различных материалов подложки эта величина будет разной. Знание распределения примеси и точечных дефектов в материале подложки после имплантации необходимо для нахождения остаточных концентрационных напряжений.2.5 Остаточные концентрационные напряженияКак правило, глубина модифицированного слоя значительно меньше размеров легированной поверхности изделия. Тогда имплантированный материал можно схематизировать как полупространство. Предполагаем, что до обработки поверхность была свободна от напряжений, а начальные концентрации дефектов и примесей равнялись нулю. При наличии примесей и дефектов поверхностный слой растягивается или сжимается и затем остается в таком состоянии. Напряжения в поверхностном слое (рисунок 2.7) описываются следующим уравнением [34]:
где σxx, σyy, σzz – нормальные напряжения, действующие
вдоль координатных осей,
Рисунок 2.7 – Остаточные концентрационные напряжения в поверхностном слое материала подложки после имплантации. Остаточные концентрационные напряжения определяют свойства материала после имплантации. Для расчета концентрационных напряжений по соотношению (2.40) необходимо определить распределение концентраций примесных атомов Ci(x) и вакансий Cv(x). Для их расчёта необходимо определить пробеги ионов, которые рассчитываются с помощью метода Монте-Карло (см. раздел 3.1). Использование этого метода позволяет учесть вероятностный характер физических процессов, протекающих при ионной имплантации в мишенях сложного химического состава, таких как металлы и сплавы. 3. Методики расчёта основных параметров физических процессов, происходящих при ионной имплантации Методики расчёта основных параметров физических процессов, происходящих при ионной имплантации основаны на следующих допущениях: 1) при прохождении иона через вещество не учитывается изменение его заряда и массы; 2) мишень считается аморфной (не учитывается кристаллическая решетка); 3) потери энергии ионом определяются только упругими и неупругими столкновениями, причём оба вклада считаются независимыми в процесс торможения; 4) ион останавливается, когда его энергия меньше потенциальной энергии взаимодействия его с атомом решётки перед столкновением; 5) изменение химического состава материала в процессе имплантации не учитывается. Допущение 1 основано на том, что после имплантации азот находится в атомарном состоянии в материале подложки. Заряд и масса имплантируемых ионов меняются не только в процессе столкновений с атомами решётки, но и при подлёте к поверхности материала за счёт эффекта нейтрализации. Учёт этих эффектов сильно осложняет расчёты, но, как показано в работах [21, 22], незначительно повлияет на их точность. Допущение 2 соответствует немонокристаллическим мишеням, таким как металлы и сплавы. Для аналитического расчета распределения по глубине мишени концентрации внедренных ионов по формуле (2.36) необходимо определить средний проецированный пробег и его страгглинг. Для одноатомных веществ можно воспользоваться соотношением (2.3). Реальные материалы имеют более сложный химический состав и физические процессы, протекающие при ионной имплантации в них имеют вероятностный характер. Для учёта этих факторов используется метод имитационного моделирования Монте-Карло. 3.1 Методика расчета пробегов ионов методом Монте-КарлоДля определения среднего проецированного пробега Rp и его отклонения ΔRp воспользуемся методом имитационного моделирования Монте-Карло. Этот метод используется для расчёта пробегов ионов в подложках сложного химического состава. Он основан на расчёте потерь энергии ионом из соотношений (2.8) и (2.34) при каждом отдельном взаимодействии с атомом мишени. При этом случайными величинами при моделировании каждого взаимодействия будут прицельный параметр р, а также характеристики очередного атома мишени М2, Z2. Такой метод имитационного моделирования позволит учесть неоднородность химического состава обрабатываемого материала. Таким образом, для моделирования процесса внедрения ионов в рамках методики расчета концентрационных напряжений воспользуемся формулой (2.36). Для определения входящих в (2.36) параметров (среднего проецированного пробега ионов и его отклонения) разработана методика расчета методом Монте-Карло. В соответствии с теорией Линхардта-Шарфа-Шиотта учитываются потери энергии только при неупругих взаимодействиях с электронами и упругих взаимодействиях с ядрами
где Т - общие потери энергии при одном взаимодействии, Дж. В качестве потенциала взаимодействия используется универсальный потенциал Томаса-Ферми (2.27), так как для него рассчитана прямая зависимость энергетических потерь от прицельного параметра (2.34). Модель одного взаимодействия иона с атомом материала подложки. Потери энергии ионом в материале подложки рассчитываются в соответствии с (3.1). После каждого взаимодействия энергия иона уменьшается на величину T. Электронные потери рассчитываются по формуле (2.34). При этом E текущая энергия иона (энергия иона до столкновения). Скорость иона рассчитывается в соответствии с энергией иона перед столкновением. Прицельный параметр p генерируется как случайная величина в пределах половины межатомного расстояния; М2, Z2 – атомный номер и атомная масса элемента вещества подложки, генерируются в соответствии с процентным содержанием элемента в материале мишени. Затем определяются Zmin и Zmax для использования в формуле (2.34). Преобразуем (2.8) к более наглядному виду для вычислений, подставив (2.9) в (2.8):
Для расчёта потерь энергии при столкновении иона с ядрами атомов мишени выполняется по формуле (3.2). Интеграл в формуле (2.21), использующейся для вычисления угла α, можно вычислить в аналитическом виде лишь для некоторых определенных зависимостей потенциала взаимодействия частиц от их взаимного расстояния. В общем виде интеграл в выражении (2.21) приходится вычислять численным методом, что не всегда легко сделать, так как подынтегральное выражение содержит особенность при r = rmin. В этом случае удобно провести следующие величины:
В результате получаем угол отклонения частицы в силовом поле в виде, удобном для численных расчётов [57]:
В данном виде подинтегральная функция не имеет особенностей [57], так как
Дифференциальное сечение рассеяния для потенциала Томаса—Ферми—Фирсова вычислено Линдхардом, Нильсоном и Шарфом [72]:
где Значения функции
где константа Из вышесказанного следует, что применение потенциала Томаса-Ферми-Фирсова наиболее целесообразно для расчёта ядерных потерь энергии ионами газов при имплантации в металлы или сплавы, так как для него рассчитана прямая зависимость энергетических потерь от прицельного параметра (2.34) и дифференциальное сечение рассеяния dσ; причём он даёт более точные результаты, чем, к примеру, потенциал Бора. В основе метода Монте-Карло лежит алгоритм расчета среднего и среднего проецированного пробега иона и его отклонения итерационным методом, основанным на расчёте энергетических потерь иона при каждом отдельном столкновении с атомом мишени. Схема алгоритма приведена на рисунке 3.1. Последовательность действий расчета среднего проецированного пробега следующая: a) случайным образом, в пределах половины межатомного расстояния, генерируется прицельный параметр p, а также характеристики очередного атома мишени (атомный номер Z2 и атомная масса М2), в соответствии с процентным содержанием элемента в материале мишени; b) определяются потери энергии по формуле (3.1); c) рассчитывается текущая энергия иона:
рассчитывается текущее значение
пробега иона, при условии
d) определяется значение среднего проецированного пробега иона:
где θ1 – угол отклонения в ЛСК, определяется по формуле (2.6); e)
если f) для расчета распределения количества ионов по глубине пункты a - f повторяются для каждого иона (количество ионов в потоке задаётся экспериментатором); g) обрабатывается полученный массив значений Rpi, при этом рассчитывается средний проецированный пробег и среднее квадратичное отклонение пробега. Расчет среднего проецированного пробега ведется по формуле (3.8) [10]:
где N - количество элементов массива (число ионов в потоке), i - номер элемента, Rpi проецированный пробег, рассчитанный по приведенному выше алгоритму для каждого иона, м.
Рисунок 3.1 – Алгоритм расчета методом Монте-Карло пробега иона в материале подложки Среднее квадратичное отклонение пробега (страгглинг пробега) рассчитывается по формуле [3]:
где Размер фазовых зерен в реальном материале, как правило, значительно превышает длину среднего проецированного пробега. На основании этого предположения предлагается методика расчета распределения концентрации внедренных ионов по глубине реального материала. 3.2 Методика расчета распределения концентрации внедренных ионов по глубине материалаРасчет распределения концентрации внедренных ионов по глубине материала будем проводить следующим образом: 1) Получим зависимости среднего проецированного пробега Rp и страгглинга пробега ΔRp ионов для данной фазы материала мишени от энергии ионов. Для получения этих зависимостей необходимо провести расчет распределения количества внедренных ионов по глубине мишени в соответствии с алгоритмом, приведенном на рисунке 3.1 и определить характеристики полученного распределения - его математическое ожидание и среднее квадратичное отклонение (по формулам 3.8 и 3.9); 2) Расчет распределения концентрации внедренных ионов будем проводить, исходя из аналитической формулы (2.36), с использованием полученных зависимостей. Для учета химического состава и фазовой структуры материала введем весовые коэффициенты для фаз, которые можно получить из процентного содержания каждой фазы в материале мишени [3]:
где Pi - процентное содержание каждой фазы в материале мишени. С учетом весовых коэффициентов соотношение (2.36) примет вид [3]:
где Ф – полная доза имплантации, м-2; n – количество фаз в материале мишени, i – номер фазы, Rpi и ΔRpi – средний проецированный пробег и его отклонение для каждой фазы, м; x - глубина проникновения ионов, м. 3) Расчет распределения концентрации дефектов (возникающих вследствие выбивания ионом межузельного атома) будем проводить, исходя из аналитической формулы (2.37). С учетом весовых коэффициентов соотношение (2.37) примет вид [3], аналогичный (3.11):
где Входящая в соотношение (3.11) и (3.12) полная доза имплантации Ф может быть определена на основании экспериментальных данных (по результатам измерения ионного тока) в соответствии с формулой (2.35). Максимальная концентрация внедрённых атомов рассчитывается по формуле (2.38). Рассчитанные по формулам (3.11) и (3.12) распределения азота и дефектов по глубине материала после имплантации используются при определении остаточных концентрационных напряжений. 3.3 Методика расчёта остаточных концентрационных напряженийКак показано в ряде литературных источников (в частности в работах [17, 36, 37]), установить связь между технологическими параметрами имплантации и механическими свойствами обработанных изделий возможно путем расчета полей концентрационных напряжений. Возникновение напряжений при имплантации обусловлено внесением в поверхностный слой обрабатываемого материала примеси и различного рода радиационных дефектов в высокой концентрации, которые деформируют кристаллическую решетку [17]. Будем считать, что глубина модифицированного слоя значительно меньше размеров обрабатываемого изделия. Тогда имплантированный инструмент можно схематизировать как полупространство. Предполагаем, что до обработки поверхность была свободна от напряжений, а начальные концентрации дефектов и примесей равнялись нулю, при наличии примесей и дефектов поверхностный слой растягивается или сжимается и затем остается в таком состоянии. Напряжения в поверхностном слое описываются уравнением (2.40). Величина δV определяется в соответствии с зависимостями,
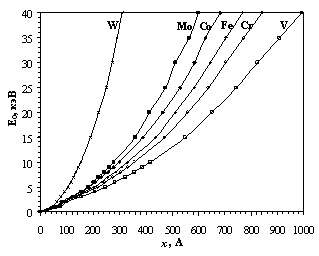
приведенными в [36]. Согласно им релаксационный объем вакансии Для расчета концентрационных напряжений необходимо определить параметры уравнения (2.40) для примесных атомов и вакансий. Таким образом, методика расчета остаточных концентрационных напряжений включает в себя: 1. Расчет по формулам (3.11) и (3.12) распределений азота и вакансий по глубине материала: Ci(x) и Cv(x). 2. Определение остаточных концентрационных напряжений по формуле (2.40). Расчет параметров физических процессов, происходящих при ионной имплантации, производился с помощью разработанного для этой цели программного обеспечения (см. Приложение 1). Результаты расчёта по описанным методикам с помощью вышеупомянутой программы приведены в следующем разделе. 4. Результаты расчёта параметров процессов взаимодействия имплантируемых ионов с материалом подложки В соответствии с предложенной методикой проведён расчёт характеристик распределения азота (средний проецированный пробег Rp и страгглинг пробега ΔRp) для встречающихся в сталях фаз при различных значениях энергий ионов с помощью программного обеспечения (приложения А и Б). Результаты расчёта приведены в таблицах 4.1 - 4.4. Таблица 4.1 - Зависимость пробегов
ионов азота от их начальной энергии в диапазоне 1 – 10 кэВ (
Таблица 4.2 - Страгглинги пробегов
ионов азота с энергией 1 – 10 кэВ (
Таблица 4.3 - Зависимость пробегов
ионов азота от их начальной энергии в диапазоне 15 – 40 кэВ (
Таблица 4.4 - Страгглинги пробегов
ионов азота с энергией 15 – 40 кэВ (
Из анализа результатов расчётов,
приведённых в таблицах 4.1 - 4.4 следует, что значение пробега существенно зависит
от элементного состава и характеристик атомов (M2, Z2) материала
подложки. Большая величина страгглингов пробегов в таблицах 4.2 и 4.4 по
сравнению с пробегами в таблицах 4.1 и 4.3 объясняется тем, что для лёгких
ионов азота, когда
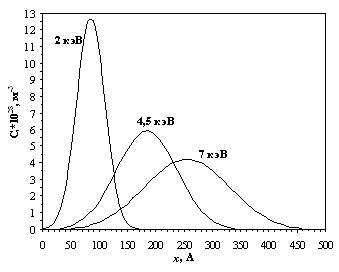
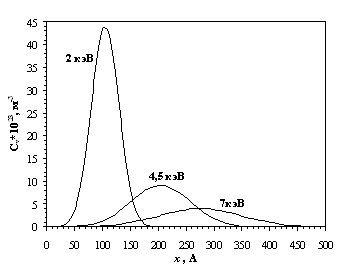
Рисунок 4.1 – Зависимость пробегов ионов азота в различных фазах, встречающихся в сталях, в зависимости от энергии имплантации. На рисунке 4.1 изображён график зависимости пробегов ионов азота в различных фазах в зависимости от энергии имплантации, построенный на основе данных из таблиц 4.1 - 4.4. Значения пробегов из таблиц 4.1 – 4.4 используются для расчёта распределения ионов азота в поверхностном слое подложки после ионной имплантации. На рисунках 4.2 и 4.3 приведены графики распределения концентрации азота и распределения дефектов по глубине подложки из стали Р6М5, полученные на основе результатов расчётов с помощью разработанного программного обеспечения (приложение 1). Вычисления проводились для энергий ионов 2, 4,5 и 7 кэВ. Доза имплантации составляла 1021 м-2.
Рисунок 4.2 – График распределения внедрённой примеси в стали Р6М5 после имплантации.
Рисунок 4.3 – График распределения дефектов в стали Р6М5 после имплантации. Анализ графиков на рисунках 4.2 и 4.3 показывает, что максимум концентрации дефектов находится приблизительно на 20 Å глубже максимума концентрации примесных атомов. Также получается, что максимальная концентрация дефектов превышает максимальную концентрацию внедрённой примеси, например, при 2 кэВ в 3,4 раза, и, с увеличением энергии, максимумы концентраций резко сближаются до почти полного совпадения при 7 кэВ. Это объясняется тем, что с увеличением начальной энергии иона уменьшается вклад ядерного торможения в общие потери энергии. Например, из (2.4) следует, что при Eкр > 1,7 кэВ для фазы α-Fe ядерные потери, которые определяют величину коэффициента kdi в (3.12), становятся пренебрежимо малыми. Таким образом для 2 кэВ большую часть общих потерь энергии составляют ядерные потери энергии, а для 7 кэВ электронные потери энергии. Из анализа графиков на рисунках 4.2 и 4.3 можно предположить, что на физико-механические характеристики поверхностного слоя образцов из стали Р6М5 более существенное влияние оказывают вакансии, чем примесные атомы, что согласуется с данными работ [3, 58, 89, 93].
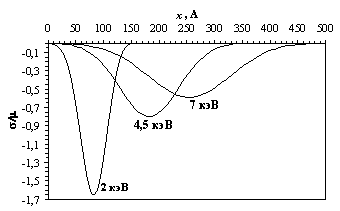
Рисунок 4.4 – График распределения остаточных концентрационных напряжений в стали Р6М5 после имплантации. По результатам расчёта распределений дефектов и примесных атомов на рисунке 4.4 построены графики остаточных концентрационных напряжений в стали Р6М5 в безразмерных координатах σ/μ, где μ – модуль Юнга стали Р6М5. Для аналогичных условий проведения процесса имплантации азота (сталь Р6М5, энергия ионов 2, 4,5 и 7 кэВ, доза имплантации 1021 м-2) в литературе [3] приведены экспериментальные данные по изменению относительной микротвёрдости η:
где HV1 – микротвёрдость образца после ионной имплантации азота, HV – микротвёрдость образца до имплантации. Экспериментальные данные по изменению относительной микротвёрдости объединены в таблице 4.5 с данными характеристик имплантации ионов азота с энергией 2, 4.5 и 7 кэВ для стали Р6М5, взятых из таблиц 4.1 - 4.4 и из анализа графиков, приведённых на рисунках 4.1 – 4.4. Таблица 4.5 - Зависимость характеристик материала подложки от энергии имплантируемых ионов
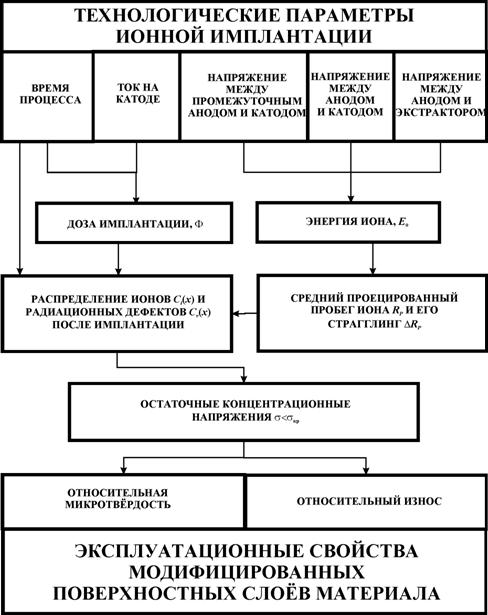
Из анализа данных, приведённых в таблице 4.5 следует, что с увеличением энергии на 2,5 кэВ относительная микротвёрдость увеличивается в среднем на 21 %. Увеличение микротвёрдости объясняется тем, что с повышением начальной энергии ионов они проникают на большую глубину, и их распределение по глубине становится более равномерным. Следовательно, более равномерно распределены и напряжения сжатия, благодаря действию которых происходит упрочнение материала. Также необходимо отметить, что с повышением энергии иона уменьшается концентрация вакансий (они создают напряжения растяжения, разупрочняющие материал), а значит уменьшается вклад создаваемых ими напряжений в остаточные концентрационные напряжения. Из анализа результатов расчётов, приведённых в таблице 4.5 и графика на рисунке 13 следует, что для стали Р6М5 при дозе имплантации 1021 м-2 максимальные остаточные концентрационные напряжения σmax меньше предела прочности при разрыве σв. Таким образом, модифицированный поверхностный слой материала подложки обладает некоторым запасом прочности и, если напряжения, которые могут возникнуть в процессе эксплуатации изделия не будут превышать σв, то изделие пригодно к эксплуатации; иначе в его поверхностном слое могут возникнуть трещины и произойдёт разрушение материала. Итак, складывая остаточные концентрационные напряжения σmax и эксплуатационные напряжения σэксп (которые определяются на месте эксплуатации), мы можем предсказать, выдержит ли материал нагрузки при эксплуатации. С помощью разработанной методики и программного ообеспечения можно решить и обратную задачу: подобрать такую энергию иона E0 и дозу имплантации Ф, при которых для данного материала σmax+σэксп<σв. Итак, в работе решена поставленная задача составление прогноза о эксплуатационном поведении материала в зависимости от ТПО. Взаимосвязь между ТПО и эксплуатационными свойствами поверхностных слоёв материала подложки изображена в виде схемы на рисунке 4.5. Чем больше ток на катоде, тем больше полная доза имплантированных ионов азота, тем выше лежат максимумы концентраций ионов и дефектов после имплантации на графиках их распределений (рисунки 4.2 и 4.3). Чем больше время процесса имплантации, тем более сглажены (максимумы понижаются) кривые распределений дефектов и остаточных концентрационных напряжений, так как в материале подложки происходят процессы рекомбинации точечных дефектов, уменьшающие их концентрацию.
Рисунок 4.5. Схема связи между технологическими параметрами обработки и эксплуатационными свойствами модифицированных поверхностных слоёв материала. Чем выше напряжение между промежуточным анодом и катодом, между анодом и катодом, между анодом и экстрактором, тем выше энергия иона, а значит больше и его пробег. Вследствие этого сглаживаются кривые распределения ионов, дефектов и остаточных концентрационных напряжений после имплантации. В конечном итоге это сказывается на повышении микротвёрдости и износостойкости поверхностных слоёв легируемого материала. В следующем разделе описано
экспериментальное оборудование, позволяющее производить имплантацию ионов азота
с энергией 1 – 10 кэВ ( 5. Экспериментальное оборудование 5.1 Установка для ионной имплантации азота в инструментальные материалыДля экспериментальной проверки
получившихся результатов создается установка для имплантации ионов азота с
энергией 1 – 10 кэВ ( 1) ионный источник (плазмотрон); 2) система электропитания ионного источника; 3) система вакуумирования; 4) устройство для измерения дозы имплантации. Ионный источник должен обеспечивать формирование и экстрагирование ионного пучка из газообразного азота при нормальных условиях рабочего вещества. Система вакуумирования должна обеспечивать остаточное давление в рабочей камере порядка 10-2 – 10-3 Па [3]. Конструкция системы электропитания установки должна обеспечивать функционирование ионного источника, подачу высокого (от 1 кВ) ускоряющего напряжения между рабочей камерой и ионным источником и безопасность персонала при работе с высоким напряжением. Устройство для измерения дозы имплантации должно обеспечивать измерение дозы с максимально возможной точностью.
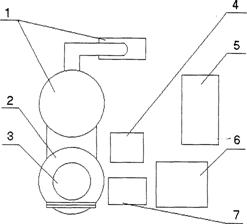
Рисунок 5.1 - Схема размещения узлов экспериментальной установки. 1 – вакуумные насосы; 2 – вакуумная камера; 3 – ионный источник; 4 источник питания плазмотрона; 5 – высоковольтный источник питания; 6 – стойка управления системой вакуумирования; 7 – блок управления системой электропитания ионного источника. В соответствии с изложенными требованиями создаётся установка для ионной имплантации ВИУ-1, схема размещения элементов которой показана на рисунке 5.1, а общий вид установки для ионной имплантации приведен на рисунке 5.2. В качестве ионного источника использован дуоплазмотрон, разработанный в МАТИ им. К.Э. Циолковского (рисунок 5.3), который предназначен для ионизации газообразных веществ. В качестве системы вакуумирования используется вакуумная установка для напыления покрытий методом КИБ ВУ-1Б, которая обеспечивает требуемое остаточное давление в вакуумной камере. В состав установки ВИУ-1 входит система электропитания дуоплазмотрона.
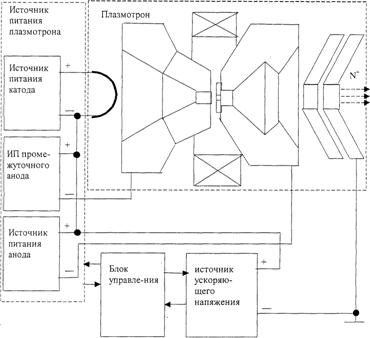
Рисунок 5.2 – Общий вид экспериментальной установки. 1 – ионный источник; 2 – вакуумная камера на базе установки ВУ–1Б; 3 – стойка управления системой вакуумирования; 4 блок управления системой электропитания ионного источника. 5.2 Устройство системы электропитания имплантационной установкиФункциональная схема системы электропитания имплантационной установки, изображенная на рисунке 5.3, включает следующие элементы: · блок управления; · источник питания плазмотрона; · высоковольтный источник питания (ВИП). Блок управления предназначен для выдачи необходимых регулирующих сигналов на источники питания плазмотрона и ВИП. Источник питания плазмотрона предназначен для поддержания на заданном уровне электрических сигналов, обеспечивающих функционирование дуоплазмотрона.
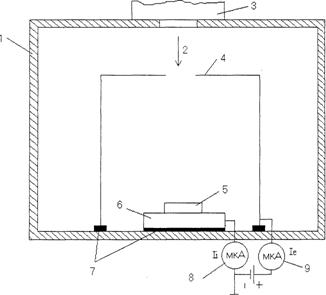
Рисунок 5.3 – Функциональная схема системы электропитания имплантационной установки. Высоковольтный источник питания предназначен для подачи на установку высокого ускоряющего напряжения. В схеме пульта управления предусмотрена возможность не только ручного, но и внешнего регулирования электрических параметров, в том числе от персонального компьютера. Система электропитания установки ВИУ-1 обеспечивает возможность реализации процесса ионной имплантации азота в инструментальные материалы с целью модификации их поверхностных свойств. Широкие диапазоны регулирования электрических параметров, позволяют проводить исследования с целью оптимизации технологии ионного модифицирования поверхностных свойств металлов и сплавов. Безопасность персонала обеспечивается оптической развязкой цепей управления от высоковольтных цепей. Для измерения дозы имплантации применено оригинальное устройство [3]. 5.3 Устройство датчика ионного токаВ установках ионной имплантации уделяется повышенное внимание измерению ионного тока, так как эти измерения, что следует из соотношения (2.35) лежат в основе правильного задания и контроля дозы имплантации. Трудность при измерении ионного тока заключаются в том, что при прямом измерении значительную (до 10 раз) ошибку вносят вторичные электроны, выбитые с поверхности мишени (эффект нейтрализации). В установке ВИУ-1 использовано устройство для измерения ионного тока, работающее по принципу цилиндра Фарадея. Схема измерительного устройства приведена на рисунке 5.4.
Рисунок 5.4 – Устройство для измерения ионного тока. 1 – вакуумная камера; 2 – ионный поток; 3 – плазмотрон; 4 – коллектор электронов; 5 – мишень; 6 – стол; 7 изоляторы; 8 – микроамперметр для измерения ионной составляющей тока; 9 – микроамперметр для измерения электронной составляющей тока. В состав устройства входят: коллектор электронов 4 (металлический цилиндр с отношением длины к диаметру 6:1), изолированный от стенок вакуумной камеры 1, источник постоянного напряжения 100 В и два микроамперметра 8 и 9 для измерения ионной и электронной составляющих тока соответственно. Отличительной особенностью измерительного устройства является то, что рабочий стол 6 с обрабатываемыми образцами 5 размещается внутри данного устройства. Разрабатываемое оборудование позволит
осуществлять имплантацию ионов азота с энергией 1 – 10 кэВ ( ЗаключениеНесмотря на большое количество
исследований в области ионной имплантации, остаётся ещё множество вопросов,
стоящих перед исследователями [3]. В частности, мало изучены процессы,
происходящие при внедрении ионов с энергией от 1 кэВ ( С помощью анализа литературы были установлены основные процессы, происходящие при ионной имплантации, разработан комплекс моделей, позволяющих перейти от ТПО к эксплуатационным свойствам материала и составить прогноз о его эксплуатационном поведении. Таким образом по работе можно сделать следующие выводы: 1. Анализ состояния вопроса поверхностной модификации свойств металлов и сплавов методом ионной имплантации азота позволил установить, что: · ионная имплантация является высокоэффективным методом поверхностной модификации; · не предложено модели модификации поверхностного слоя металлов и сплавов в результате имплантации ионов азота, наиболее полно учитывающей процессы, происходящие при этом; · формулы, связывающие параметры ионной имплантации с пробегами ионов в мишенях действуют лишь в определённых энергетических диапазонах; поэтому необходимо внимательно следить за областью их применения в расчётах; ·
недостаточно исследована
возможность применения имплантации ионов газов с энергией в диапазоне 1 – 10 кэВ
( 2. Предложена модель модификации поверхностного слоя металлов и сплавов в результате имплантации ионов азота, которая позволяет при заданных технологических параметрах имплантации спрогнозировать эксплуатационные свойства металла или сплава; 3.
На основе анализа
литературы разработана методика, позволяющая наиболее точно рассчитать по
предложенной модели параметры основных процессов, происходящих при ионной
имплантации азота с энергией 1 – 10 кэВ ( 4. Для выполнения расчётов разработано программное обеспечение (приложения А и Б), позволяющее при заданных ТПО рассчитать остаточные концентрационные напряжения, возникающие при имплантации ионов азота в металлы и сплавы; 5. Полученные теоретические результаты согласуются с данными, приведёнными в литературе, с точностью в пределах 10 – 15 %, что свидетельствует об адекватности построенной модели. Несмотря на то, что мы не учитывали процесс дальнодействия, разработанная методика позволяет с достаточной степенью точности рассчитать основные параметры процессов, происходящих при ионной имплантации и предсказать на основе их значений эксплуатационные свойства материала. Ионная имплантация обладает очень широкими возможностями для изменения свойств материалов. При ионной имплантации газов в поверхностном слое металлов и сплавов создаются условия, способствующие протеканию реакций между атомами внедренной примеси и атомами матрицы, а также растворенными в ней примесями. Это позволяет легировать металл или сплав ионами недостающего для образования соединения элемента; синтезировать как известные соединения, так и соединения, которые не могут быть созданы другими методами. Ионная имплантация может быть применена для получения равновесных и метастабильных фаз с существенно расширенными границами правила Юм-Розери по сравнению с его применением при традиционных способах образования твердых растворов. Эмпирическое правило Юм-Розери для образования метастабильного твердого раствора при ионной имплантации: "Метастабильный твердый раствор образуется, если имплантированная примесь имеет: а) атомный радиус в пределах от 15 до 40 % от радиуса матрицы, б) электроотрицательность в пределах ±0,6 от атомов матрицы". Таким образом, благодаря возможности воздействия на механические и химические свойства, фазовый состав и структуру поверхностных слоев металлов и сплавов метод ионной имплантации, не ограниченный условиями равновесных фазовых диаграмм, открывает широкие возможности для целенаправленного и управляемого изменения поверхностных свойств металлов и сплавов, синтеза новых метастабильных растворов и создания новых материалов с необычными свойствами. Список Литературы 1. Ионная имплантация. Сб. статей. Пер. с англ. / под ред. Хирвонена Д.М.: Металлургия, 1985. 2. Хирвонен Дж.К. Ионная имплантация. М.: Металлургия, 1985. 285 с. 3. Инзарцев Ю.В. Повышение эксплуатационных характеристик инструмента методом ионной имплантации азота. Дисс. канд. техн. наук. / Тульский Государственный Университет – Тула. 2002. –129 с. 4. Лахтин Ю.М., Леонтьева В.П. Материаловедение: Учебник для высших технических учебных заведений. – 3-е изд., перераб. и доп. – М.: Машиностроение, 1990. – 528 с.: ил. 5. Модифицирование и легирование поверхности лазерными, ионными и электронными пучками / Под. ред. Дж. М. Поута, Г. Фоти, Д.К. Джекобсона. М: Машиностроение, 1987. 424с. 6. Комаров Ф.Ф. Ионная имплантация в металлы. - М.: Металлургия, 1990. 134с. 7. Афанасьев В.П., Манухин В.В., Нуекс Д. Взаимодействие лёгких ионов средних энергий с неоднородными поверхностями // Инженерные проблемы термоядерной энергетики. М.: МЭИ, 1989. №220. С. 27-32. 8. Погребняк А.Д., Ремнев Г.Е., Чистяков С.А., Лигачёв А.Е. Модификация свойств металлов под действием ионных пучков // Изв. ВУЗов. Физика. 1987. №1. С. 52-65. 9. Калачев М.И. Деформационное упрочнение металлов. Мн., Наука и техника, 1980, 256 с. 10. Теория термической обработки. Учебник для вузов. Блантер М.Е. М.: Металлургия, 1984, 328с. 11. Бельский Е.И., Ситкевич М.В., Понкратин Е.И., Стефанович В.А. Химико-термическая обработка инструментальных материалов.-Мн.: Наука и техника, 1986.-247 с. 12. Теория и технология азотирования / Лахтин Ю.М., Коган Я.Д, Шпис Г.И., Бемер 3. - М.: Металлургия, 1991, 320с. 13. X. Риссел, И. Руге. Ионная имплантация: Пер. с нем. В.В. Климова, В.Н. Пальянова. / Под ред. М.И. Гусевой. - М.: Наука. Главная редакция физико-математической литературы, 1983. - 360с. 14. Кумахов М.А., Комаров Ф.Ф. Энергетические потери и пробеги ионов в твердых телах. - Мн.: Изд-во БГУ, 1979.-320с. 15. Костерин К.В. Распыление твердых тел ионной бомбардировкой: адатомные механизмы и возможная роль фононов. // Физика и химия обработки материалов № 3 - 1995. с. 43-48. 16. Оборудование ионной имплантации/ В.В. Симонов, Л.А. Корнилов, А.В. Шашелев, Е.В. Шокин. - М.: Радио и связь, 1988. - 184с. 17. Распыление твердых тел ионной бомбардировкой: Пер. с англ. / Под ред. Р. Бериша. - М.: Мир, 1986. - 488 с. 18. Барвинок В. А. Управление напряженным состоянием и свойства плазменных покрытий. -М.: Машиностроение, 1990.-384 с. 19. Сулима A.M., Шулов В.А. Ионное легирование конструкционных материалов.// Поверхностный слой, точность, эксплуатационные свойства и надежность деталей машин и приборов. - М.: МДНТП, 1989. -с. 73-78. 20. Никитин А.А., Травина Н.Г. Ионная имплантация металлов и сплавов. // Бюллетень ЦНИИЧ. - 1986. - № 23. 21. Васильева Е.В. Влияние имплантации ионов азота и углерода на стойкость подшипниковой стали // Физика и химия обработки материалов №1. – 1989. с. 43-48. 22. Зеленский В.Ф., Неклюдов И.М., Черняева Т.П. Радиационные дефекты и распухание металлов. - Киев: Наукова думка, 1988. - 296 с. 23. Синебрюхов А.А., Харлов А.В., Бурков П.В. Исследование модификации поверхности быстрорежущей стали под воздействием ионного пучка// Материалы международного научно-технического симпозиума Славянтрибо-4. Трибология и технология. С.-Пб. 1997, Т. 1. с.74-77. 24. Lindhard J., Scharff M., Schiott H.E. - Mat. -Fys. Medd. Dan. Vid. Selsk, 1963, 33, N 14. 25. Lindhard J., Scharff M. - Phys. Rev., 1961, v. 124, p. 128. 26. Каминский М.А. Атомные и ионные столкновения на поверхности металлов. -М.: Мир, 1967. 506 с. 27. Титов В.В. Роль механических напряжений при легировании материалов с помощью ионных пучков. М.: Препринт ИЛЭ им. И.В. Курчатова, 1983. 48с. 28. Бобровский С.М. Повышение эксплуатационных свойств режущего инструмента методом ионной имплантации. Дисс. канд. техн. наук. / Тольятти. – 1998. – 245 с. 29. Смирнов М.Ю. Повышение работоспособности торцовых фрез путем совершенствования конструкций износостойких покрытий: дисс. к.т.н. Ульяновск, 2000. - 232 с., ил. 30. Буренков Л.Ф., Комаров Ф.Ф., Кумахов М.А., Темкин М.М. Таблицы параметров пространственного распределения ионно-имплантированных примесей. Минск.: БГУ, 1980. 348 с. 31. Готт Ю.В., Явлинский Ю.Н. Взаимодействие медленных частиц с веществом и диагностика плазмы. М., 1973. 32. Sommerfeld A. - Rend. Acad. Lincei, 1935, 6,759. 33. Caspar R. - Acta Phys. Hung., 1952, 11,151. 34. Teitz T. -Ann. d.Phys., 1955, 15, 186. 35. Wedephol P. - J. Phys., 1968, B1, 307. 36. Белый А.В., Догодейко В.Г., Макушок Е.М., Миневич А.Л. Прогрессивные методы изготовления металлорежущего инструмента. Минск.: БЕЛНИИТИ, 1989. 56 с. 37. Ландау Л. Д., Лифшиц Е. М. Квантовая механика. М., Физматгиз, 1963. 38. Ландау Л. Д., Лифшиц Е. М. Механика. М., Физматгиз, 1958. 39. Lindhard J., Nielsen V., Scharff М. Mat.-fys. Medd. Dan. Vid. Sel., 1968, 36, №10. 40. Фирсов О. Б. "Ж. эксперим. и теор. физ.", 1959, 36, 1517. 41. Кишиневский Л. М. "Изв. АН СССР. Сер. физ.", 1962, 26, 1410. 42. Абов Ю.Г., Иванов Л.И., Заболотный В.Т., Суворов А.Л. Динамические процессы при облучении твёрдых тел. Препринт №81. М.: ИТЭФ, 1985. 52 с. 43. Бабаев В.П., Бобков А.Ф., Заболотный В.Т. и др. Каскады атомных столкновений в металлах. М.: Препринт ИТЭФ-110, 1982, 40 с. 44. Иолфи Ф.В. Фазовые превращения при облучении. - Челябинск: Металлургия, 1989.312 с. 45. Искандерова З.А., Раджабов Т.Д., Рахимова Г.Р. Формирование упрочненного приповерхностного слоя с выделениями новой фазы на объемных дефектах при ионной имплантации. Поверхность. - 1985. - №10. с. 115-126. 46. Лейман К. Взаимодействие излучения с твердым телом и образование элементарных дефектов: Пер. с англ.-М.: Атомиздат, 1979. 296 с. 47. Константы взаимодействия металлов с газами: Справ, изд. Коган Я.Д., Колачев Б.А., Левинский Ю.В. и др. - М.: Металлургия, 1987. - 368 с. 48. Бойко В.И., Кадлубович Б.Е., Шаманин И.В. Влияние дефектности структуры металлов на профиль расперделения внедренных ионов. // Физика и химия обработки материалов № 3 - 1991. с. 56-61. 49. Влияние никоэнергетической имплантации на механические свойства сплавов титана и железа. / В.О. Вальднер, В.П. Квядрас и др.// Физика и химия обработки материалов. - 1987. - № 2 -с. 18-24. 50. Бериш Р. Распыление твёрдых тел ионной бомбардировкой. М.: Мир, 1986. Т. 2. 484 с. 51. Баранов И.А., Мартыненко Ю.В., Цепелевич С.О., Явлинский Ю.Н. Неупругое распыление твёрдых тел ионами // УФН. 1988. Т. 156. С. 477-511. 52. Лариков Л.Н., Исайчев В.И. // Диффузия в металлах и сплавах: Справочник. Киев: Наукова думка, 1986. - 565 с. 53. Ноздрин В.Ф., Умеренко С.М., Губенко С.И. О механизме упрочнения металлов при сверхглубоком проникновении высокоскоростных частиц. // Физика и химия обработки материалов 6 - 1991. с. 73-79. 54. Абдрашитов В.Г., Рыжов В.В., Моделирование распределений ионной имплантации методом Монте-Карло.// Физика и химия обработки материалов № 2 - 1993. с. 22-26. 55. Диденко А.Н., Лигачёв А.Е., Куракин И.Б. Воздействие пучков заряженных частиц на поверхность металлов и сплавов. М.: Энергоатомиздат, 1987. 184 с. 56. Диденко А.Н., Шулов В.А., Ремнев Г.Е., Ночевная Н.А. Модификация свойств конструкционных материалов пучками заряженных частиц. Свердловск: ГКНТ СССР, 1991. Т. 3. С. 3. 57. Тушинский Л.И. Теория и технология упрочнения металлических сплавов. - Новосибирск: Наука, 1990. 306 с. 58. Ершов Г.С., Бычков Ю.Г., Физико-химические основы рационального легирования сталей и сплавов М.: Металлургия, 1982. 360 с. 59. Ионное облучение инструмента из быстрорежущей стали. / Н.В. Плешивцев, Д.В. Бондарев, П.П. Сидоров, С.Е. Дукачев, Г.Л. Давыдов // СТИН. - 1994. - № 6. - с. 21-23. 60. Ибрагимов Ш.Ш., Кирсанов В.В., Пятилетов Ю.С. Радиационная повреждаемость металлов и сплавов. М.: Энергоатомиздат, 1985. 240 с. 61. Дидык А.Ю., Регель В.Р., Скуратов В.А., Михайлова Н.Ю. Радиационное упрочнение металлов, облучённых тяжёлыми ионами // ЖТФ. 1989. Т. 59. №5. С. 107-111. 62. Аксёнов А.И., Бугаев С.П., Емельянов В.А. и др. Получение широкоапертурных пучков ионов металлов // ПТЭ. 1987. №3. С. 139-142. 63. Бабаев В.П., Заболотный В.Т., Суворов А.Л. Фокусировка в каскадах атомных столкновений // Вопр. атомной науки и техники. Сер. ФРПРМ. 1985. Вып. 4(37). С. 7-9. 64. Геринг Г. И., Полещенко К.Н., Вершинин Г. А., Поворознюк С. Н., Орлов П.В. Роль диффузионных процессов в повышении износостойкости модифицированных твердых сплавов // Трение и износ, 1998. Т. 19. №4. С. 453-457. 65. Заболотный В.Т., Иванов Л.P, Суворов А.Л. Автоионная микроскопия и фундаментальные аспекты повреждаемости твердых тел. // Физика и химия обработки материалов № 2 - 1994. с. 34-39. ПРИЛОЖЕНИЯ ПРИЛОЖЕНИЕ АПрограмма ION_IMPLANTATION, разработанная в среде Borland C++ для расчёта остаточных концентрационных напряжений в поверхностных слоях материала подложки после имплантации ионов азота #include <vcl\vcl.h> #include <stdlib.h> #include <math.h> #pragma hdrstop #include "Main_Form.h" #include "About.h" #pragma resource "*.dfm" TIonImpl *IonImpl; AnsiString InfoTemp,EInf; int i,j,k,l,m,n,o,p,ENum=0,EndInf=0,VInf_N,X_coord; AnsiString SubInf[14][4]; double LP, AC, AM, AR, Density, IE, IC, IM, IR, INum, IBD, SAD, E_EW, NE_EW, Rmin, IV, E_Step, E_Cntr, E_Int, E_ND, Energy, TgtPrm, TgtPrmRange, TgtPrmMIN, TgtPrmMAX, TPPrc, Rm_Range, Rm_Cntr, Rm_ND, Rm_IL, Rm_SL, Rm_Step, Rm,Differ, DifferTemp, Temp, Temp1, Temp2, Ci, Cv, sigma_max, Ci_max, Cv_max, ro_ND, ro_IL, ro_SL, ro_Range, ro_Cntr, ro_Step, fi, fi_ND, fi_IL, fi_SL, fi_Range, fi_Cntr, fi_Step, fi_Int, lambda, epsilon, ro, alpha, ksi_e, P, B, H, U, r, f_psi_arg, InactE, RelE, E_EW_Int, ShldPrm_tf, ShldPrm_f, func_ls_prm, func_ls, Tmax, psi, psi_S, psi_G, psi_T, psi_W, R, Rp, EW, tau, E_NE, R_sqr, delta_R, delta_Rp, LP_gpu, En=0, En_Temp=0, Rmin_0, VInf[14][3]; const struct EquivalentTable { double A, AMU, EV, EC; } ET = {1E-10,1.66053E-27,1.602192E-19,1.602192E-19}; double ShldPrm0=0.529E-10,eps0=8.85E-12,eps=1,EC=ET.EC,PI=3.14159,V0=2.2E6,Vv_relax=-0.05,Vi_relax=1.10,MU,V_atom,Ed=6.408768E-18; double fTFF(double R) { //Аргумент Фирсова функции экранирования Томаса-Фарми-Фирсова f_psi_arg=R/ShldPrm_tf;//(Firsov's psi argument) //Аппроксимации функции экранирования Томаса-Фарми-Фирсова //Аппроксимация Зоммерфельда Temp1=f_psi_arg/pow(12,double(2)/double(3)); Temp2=1+pow(Temp1,0.772); psi_S=pow(Temp2,-3.885);//psi of Sommerfeld //Аппроксимация Гаспара Temp1=-0.1837*f_psi_arg; Temp2=1+1.05*f_psi_arg; psi_G=exp(Temp1)/Temp2;//psi of Gaspar //Аппроксимация Тейтца Temp=1+f_psi_arg*pow(PI/double(8),double(2)/double(3)); psi_T=pow(Temp,-2);//psi of Teitz //Аппроксимация Видефола Temp=-6.62*pow(f_psi_arg,0.25); psi_W=317*f_psi_arg*exp(Temp);//psi of Wedephol //Функция экранирования Томаса-Фарми-Фирсова psi=psi_T; return psi; } __fastcall TIonImpl::TIonImpl(TComponent* Owner) : TForm(Owner) { } void __fastcall TIonImpl::About1Click(TObject *Sender) { AboutBox->ShowModal(); } void __fastcall TIonImpl::ResultClick(TObject *Sender) { if (EndInf) {ENum=0;VInf_N=0;} //Get data //Element Information Elem_Info->SelectAll(); InfoTemp=Elem_Info->SelText; EInf=InfoTemp; SubInf[ENum][0]=EInf; Elem1_Name->Caption=SubInf[0][0]; Elem2_Name->Caption=SubInf[1][0]; Elem3_Name->Caption=SubInf[2][0]; Elem4_Name->Caption=SubInf[3][0]; Elem5_Name->Caption=SubInf[4][0]; Elem6_Name->Caption=SubInf[5][0]; Elem7_Name->Caption=SubInf[6][0]; Elem8_Name->Caption=SubInf[7][0]; Elem9_Name->Caption=SubInf[8][0]; Elem10_Name->Caption=SubInf[9][0]; Elem11_Name->Caption=SubInf[10][0]; Elem12_Name->Caption=SubInf[11][0]; Elem13_Name->Caption=SubInf[12][0]; Elem14_Name->Caption=SubInf[13][0]; //Lattice Parameter 1 LatParam1->SelectAll(); InfoTemp=LatParam1->SelText; LP=InfoTemp.ToDouble(); //Lattice Parameter 2 LatParam2->SelectAll(); InfoTemp=LatParam2->SelText; LP_gpu=InfoTemp.ToDouble(); //Atom Charge AtomCharge->SelectAll(); InfoTemp=AtomCharge->SelText; AC=InfoTemp.ToDouble(); //Atom Mass AtomMass->SelectAll(); InfoTemp=AtomMass->SelText; AM=InfoTemp.ToDouble(); //Atom Radius AtomRadius->SelectAll(); InfoTemp=AtomRadius->SelText; AR=InfoTemp.ToDouble(); //Atoms In Low Level Cell AILLCell->SelectAll(); InfoTemp=AILLCell->SelText; Density=InfoTemp.ToDouble(); //Ion Energy IonEnergy->SelectAll(); InfoTemp=IonEnergy->SelText; IE=InfoTemp.ToDouble(); //Ion Charge IonCharge->SelectAll(); InfoTemp=IonCharge->SelText; IC=InfoTemp.ToDouble(); //Ion Mass IonMass->SelectAll(); InfoTemp=IonMass->SelText; IM=InfoTemp.ToDouble(); //Ion Radius IonRadius->SelectAll(); InfoTemp=IonRadius->SelText; IR=InfoTemp.ToDouble(); //Ion Number IonNum->SelectAll(); InfoTemp=IonNum->SelText; INum=InfoTemp.ToDouble(); //Ion Beam Density IonBeamDensity->SelectAll(); InfoTemp=IonBeamDensity->SelText; IBD=InfoTemp.ToDouble(); //Processing data if ((IE<10)&&(IE>0)) VInf_N=IE/1000; LP*=ET.A; AR*=ET.A; IR*=ET.A;//To Angstrems AM*=ET.AMU; IM*=ET.AMU;//To Atomic Mass Unit IE*=ET.EV;//To Electron-Volt SAD=Density/AM;//Substrate Atoms Density V_atom=4/3*PI*pow(AR,3); R=0;Rp=0;delta_R=0;delta_Rp=0;En=0; ResultData->Lines->Append(InfoField6->Caption); ResultData->Lines->Append(IE); //Ion implantation task solution //Общие константы lambda=1.309; ksi_e=pow(IC,double(1)/double(6)); //Рассчёт параметра экранирования Temp=pow(IC,double(2)/double(3))+pow(AC,double(2)/double(3)); ShldPrm_tf=0.8853*ShldPrm0/pow(Temp,double(1)/double(2));//Параметр экранирования Томаса-Ферми Temp=pow(IC,double(1)/double(2))+pow(AC,double(1)/double(2)); ShldPrm_f=0.8853*ShldPrm0/pow(Temp,double(2)/double(3));//Параметр экранирования Фирсова randomize();//Инициализация счётчика случайных чисел TPPrc=11;//Target Parameter Precision //Вычисление минимального значения прицельного параметра TgtPrmMIN=0; //Вычисление максимального значения прицельного параметра TgtPrmMAX=LP/2; //Интервал значений прицельного параметра TgtPrmRange=TgtPrmMAX-TgtPrmMIN; for (k=1;k<=INum;k++) { //Начало цикла по энергии. //Потери энергии вычисляются в соответствии с типом модели. E_ND=100;//Число разбиений (Number of Divisions) E_Cntr=IE;//Счётчик (Counter) E_Step=IE/E_ND;//Приращение (Step) E_Int=0; for (i=E_ND;i>=1;i--) { Energy=E_Cntr-E_Step/2;//Ion Energy Rm_IL=0;//Rmin First Value Rm_SL=LP/2;//Rmin Last Value Rm_Range=Rm_SL-Rm_IL; Rm_ND=100; DifferTemp=1; Rm_Step=Rm_Range/Rm_ND; Rm_Cntr=Rm_IL+Rm_Step; for (j=1;j<=Rm_ND;j++) { Rm=Rm_Cntr-Rm_Step/2; Temp=1-(IC*AC*pow(EC,2)*fTFF(Rm)*(IM+AM))/(4*PI*eps*eps0*Rm*Energy*AM); Differ = (Temp<0) ? -Temp : Temp; if (Differ<DifferTemp) {DifferTemp=Differ; Rmin_0=Rm;} Rm_Cntr+=Rm_Step; } IV=sqrt(2*Energy/IM); Temp=pow(IC,double(2)/double(3))+pow(AC,double(2)/double(3)); NE_EW=(8*PI*ShldPrm0*SAD*ksi_e*IC*AC*pow(EC,2)*IV)/(V0*4*PI*eps*eps0*pow(Temp,double(3)/double(2)));//Неупругие потери E_NE=0.525*pow(Temp,2)*pow(IM,2)*EC*1E3/(pow(ksi_e,2)*pow(IM+AM,2)); E_EW=0;En_Temp=0; if (Energy<E_NE) { //Потери энергии при столкновениях (модель Томаса-Ферми-Фирсова) ro_ND=100;//Число разбиений (Number of Divisions) ro_IL=0; ro_SL=LP/2-Rmin_0;//Пределы интегрирования: Inferior Limit - нижний, Superrior Limit - верхний ro_Range=ro_SL-ro_IL; //Длина интервала ro_Cntr=ro_IL+ro_Range/ro_ND; ro_Step=ro_Range/ro_ND;//Счётчик и приращение E_EW_Int=0; for (l=1;l<=ro_ND;l++) { ro=ro_Cntr-ro_Step/2;//Переменная цикла //Вычисление расстояния максимального сближения частиц Rm_IL=0;//Rmin First Value Rm_SL=LP/2;//Rmin Last Value Rm_Range=Rm_SL-Rm_IL; Rm_ND=100; DifferTemp=1; Rm_Step=Rm_Range/Rm_ND; Rm_Cntr=Rm_IL+Rm_Step; for (j=1;j<=Rm_ND;j++) { Rm=Rm_Cntr-Rm_Step/2; Temp=1-pow(ro/Rm,2)-(IC*AC*pow(EC,2)*fTFF(Rm)*(IM+AM))/(4*PI*eps*eps0*Rm*Energy*AM); Differ = (Temp<0) ? -Temp : Temp; if (Differ<DifferTemp) {DifferTemp=Differ; Rmin=Rm;} Rm_Cntr+=Rm_Step; } //Потенциал Томаса-Ферми-Фирсова U=IC*AC*pow(EC,2)*fTFF(Rmin)/(4*PI*eps*eps0*Rmin); fi_ND=100;//Число разбиений (Number of Divisions) fi_IL=Rmin; fi_SL=1E-9;//Пределы интегрирования: Inferior Limit - нижний, Superrior Limit - верхний fi_Range=fi_SL-fi_IL; //Длина интервала fi_Cntr=fi_IL+fi_Range/fi_ND; fi_Step=fi_Range/fi_ND;//Счётчик и приращение fi_Int=0; for (p=1;p<=fi_ND;p++) { fi=fi_Cntr-fi_Step/2;//Переменная цикла Temp=1-pow(ro/fi,2)-IC*AC*pow(EC,2)*fTFF(fi)*(IM+AM)/(4*PI*eps*eps0*Energy*AM*fi); Temp = (Temp<0) ? -Temp : Temp; fi_Int+=(ro/pow(fi,2))*fi_Step/sqrt(Temp); fi_Cntr+=fi_Step;//Приращение переменной цикла } alpha=PI-2*fi_Int; alpha = (alpha<0) ? -alpha : alpha; Temp=sin(alpha/2); En_Temp+=4*Energy*IM*AM*pow(Temp,2)/pow(IM+AM,2); E_EW_Int+=pow(Temp,2)*ro*ro_Step; ro_Cntr+=ro_Step;//Приращение переменной цикла } En_Temp/=100; E_EW=8*PI*IM*AM*SAD*Energy*E_EW_Int/pow(IM+AM,2);//Упругие потери (Elastic Energy Waste) } En+=En_Temp; EW=NE_EW+E_EW; Temp=(1/EW)*E_Step; E_Int+=Temp; E_Cntr-=E_Step; } //Конец цикла по энергии. //Пробег и проецированный пробег ионов R+=E_Int; Temp1=double(AM/IM); Rp+=R/(1+0.36*pow(Temp1,1.15)); } //Конец цикла по прицельному параметру. //Средний пробег и проецированный пробег ионов R/=INum; Rp/=INum; Temp=double(3-1)/double(3*(2*3-1))*4*IM*AM/pow(IM+AM,2); delta_R=sqrt(Temp)*R; delta_Rp=sqrt(Temp)*Rp; ResultData->Lines->Append("Средний пробег ионов:"); ResultData->Lines->Append(R); ResultData->Lines->Append("Страгглинг среднего пробега ионов:"); ResultData->Lines->Append(delta_R); ResultData->Lines->Append("Средний проецированный пробег ионов:"); ResultData->Lines->Append(Rp); ResultData->Lines->Append("Страгглинг среднего проецированного пробега ионов:"); ResultData->Lines->Append(delta_Rp); SubInf[ENum][2]=Rp;SubInf[ENum][3]=delta_Rp; VInf[ENum][0]=Rp+20E-10;VInf[ENum][1]=delta_Rp;VInf[ENum][2]=En/(2*Ed)/100; ENum++; } void __fastcall TIonImpl::Save1Click(TObject *Sender) { ResultData->Lines->SaveToFile("Ion_Run_Calculation_Results.txt"); } void __fastcall TIonImpl::PropsClick(TObject *Sender) { Elem1_Info->SelectAll();InfoTemp=Elem1_Info->SelText;SubInf[0][1]=InfoTemp; Elem2_Info->SelectAll();InfoTemp=Elem2_Info->SelText;SubInf[1][1]=InfoTemp; Elem3_Info->SelectAll();InfoTemp=Elem3_Info->SelText;SubInf[2][1]=InfoTemp; Elem4_Info->SelectAll();InfoTemp=Elem4_Info->SelText;SubInf[3][1]=InfoTemp; Elem5_Info->SelectAll();InfoTemp=Elem5_Info->SelText;SubInf[4][1]=InfoTemp; Elem6_Info->SelectAll();InfoTemp=Elem6_Info->SelText;SubInf[5][1]=InfoTemp; Elem7_Info->SelectAll();InfoTemp=Elem7_Info->SelText;SubInf[6][1]=InfoTemp; Elem8_Info->SelectAll();InfoTemp=Elem8_Info->SelText;SubInf[7][1]=InfoTemp; Elem9_Info->SelectAll();InfoTemp=Elem9_Info->SelText;SubInf[8][1]=InfoTemp; Elem10_Info->SelectAll();InfoTemp=Elem10_Info->SelText;SubInf[9][1]=InfoTemp; Elem11_Info->SelectAll();InfoTemp=Elem11_Info->SelText;SubInf[10][1]=InfoTemp; Elem12_Info->SelectAll();InfoTemp=Elem12_Info->SelText;SubInf[11][1]=InfoTemp; Elem13_Info->SelectAll();InfoTemp=Elem13_Info->SelText;SubInf[12][1]=InfoTemp; Elem14_Info->SelectAll();InfoTemp=Elem14_Info->SelText;SubInf[13][1]=InfoTemp; //Elasticity K_Elasticity->SelectAll(); InfoTemp=K_Elasticity->SelText; MU=InfoTemp.ToDouble(); //График концентрации внедрённой примеси GrphArea1->Canvas->MoveTo(50,250);GrphArea1->Canvas->LineTo(350,250); GrphArea1->Canvas->MoveTo(50,250);GrphArea1->Canvas->LineTo(50,20); for (i=-2;i<=2;i++) { j=(i<0) ? -i : i; GrphArea1->Canvas->MoveTo(350,250);GrphArea1->Canvas->LineTo(350-5-j,250+i); GrphArea1->Canvas->MoveTo(50,20);GrphArea1->Canvas->LineTo(50+i,20+5+j); } for (i=0;i<=280;i+=10) { GrphArea1->Canvas->MoveTo(50+i,248); GrphArea1->Canvas->LineTo(50+i,252); } for (i=0;i<=220;i+=10) { GrphArea1->Canvas->MoveTo(48,250-i); GrphArea1->Canvas->LineTo(52,250-i); } Ci_max=0; for (i=0;i<=ENum-1;i++) { Ci_max+=(IBD/sqrt(2*PI))*(SubInf[i][1].ToDouble()/100/SubInf[i][3].ToDouble()); } ResultData->Lines->Append("Максимальная концентрация внедрённой примеси:"); ResultData->Lines->Append(Ci_max); GrphArea1->Canvas->MoveTo(50,250); for (j=1;j<=300;j++) { Temp=j*ET.A*2; Ci=0; for (i=0;i<=ENum-1;i++) { Temp1=Temp-SubInf[i][2].ToDouble(); Ci+=(IBD/sqrt(2*PI))*(SubInf[i][1].ToDouble()/100/SubInf[i][3].ToDouble()*exp(-pow(Temp1,2)/(2*pow(SubInf[i][3].ToDouble(),2)))); } X_coord=Ci/1E28*10; if ((double(j)/double(5)-int(j/5))==0) ResultData->Lines->Append(X_coord); GrphArea1->Canvas->LineTo(50+j,250-int(X_coord)); } //График концентрации вакансий GrphArea2->Canvas->MoveTo(50,250);GrphArea2->Canvas->LineTo(350,250); GrphArea2->Canvas->MoveTo(50,250);GrphArea2->Canvas->LineTo(50,20); for (i=-2;i<=2;i++) { j=(i<0) ? -i : i; GrphArea2->Canvas->MoveTo(350,250);GrphArea2->Canvas->LineTo(350-5-j,250+i); GrphArea2->Canvas->MoveTo(50,20);GrphArea2->Canvas->LineTo(50+i,20+5+j); } for (i=0;i<=280;i+=10) { GrphArea2->Canvas->MoveTo(50+i,248); GrphArea2->Canvas->LineTo(50+i,252); } for (i=0;i<=220;i+=20) { GrphArea2->Canvas->MoveTo(48,250-i); GrphArea2->Canvas->LineTo(52,250-i); } Cv_max=0; for (i=0;i<=ENum-1;i++) { Cv_max+=(VInf[i][2]*IBD/(sqrt(2*PI)*VInf[i][1])); } ResultData->Lines->Append("Максимальная концентрация вакансий:"); ResultData->Lines->Append(Cv_max); GrphArea2->Canvas->MoveTo(50,250); for (j=1;j<=300;j++) { Temp=j*ET.A*2; Cv=0; for (i=0;i<=ENum-1;i++) { Temp1=Temp-VInf[i][0]; Cv+=(VInf[i][2]*IBD/(sqrt(2*PI)*VInf[i][1]))*exp(-pow(Temp1,2)/(2*pow(VInf[i][1],2))); } X_coord=Cv/1E28*4; if ((double(j)/double(5)-int(j/5))==0) ResultData->Lines->Append(X_coord); GrphArea2->Canvas->LineTo(50+j,250-int(X_coord)); } //График остаточных концентрационных напряжений GrphArea3->Canvas->MoveTo(50,20);GrphArea3->Canvas->LineTo(350,20); GrphArea3->Canvas->MoveTo(50,20);GrphArea3->Canvas->LineTo(50,250); for (i=-2;i<=2;i++) { j=(i<0) ? -i : i; GrphArea3->Canvas->MoveTo(350,20);GrphArea3->Canvas->LineTo(350-5-j,20+i); GrphArea3->Canvas->MoveTo(50,250);GrphArea3->Canvas->LineTo(50+i,250-5-j); } for (i=0;i<=280;i+=10) { GrphArea3->Canvas->MoveTo(50+i,18); GrphArea3->Canvas->LineTo(50+i,22); } for (i=0;i<=220;i+=8) { GrphArea3->Canvas->MoveTo(48,20+i); GrphArea3->Canvas->LineTo(52,20+i); } sigma_max=-2*V_atom*MU*(Vv_relax*Cv_max+Vi_relax*Ci_max); ResultData->Lines->Append("Максимальное значение остаточных концентрационных напряжений:"); ResultData->Lines->Append(sigma_max); GrphArea3->Canvas->MoveTo(50,20); for (j=1;j<=300;j++) { Temp=j*ET.A*2; Ci=0; Cv=0; for (i=0;i<=ENum-1;i++) { Temp1=Temp-SubInf[i][2].ToDouble(); Ci+=(IBD/sqrt(2*PI))*(SubInf[i][1].ToDouble()/100/SubInf[i][3].ToDouble()*exp(-pow(Temp1,2)/(2*pow(SubInf[i][3].ToDouble(),2)))); Temp2=Temp-VInf[i][0]; Cv+=(VInf[i][2]*IBD/(sqrt(2*PI)*VInf[i][1]))*exp(-pow(Temp2,2)/(2*pow(VInf[i][1],2))); } X_coord=-2*V_atom*(Vv_relax*Cv+Vi_relax*Ci)*80; if ((double(j)/double(5)-int(j/5))==0) ResultData->Lines->Append(X_coord); GrphArea3->Canvas->LineTo(50+j,20-int(X_coord)); } EndInf=1; } ПРИЛОЖЕНИЕ БРезультаты работы Программы ION_IMPLANTATION для стали Р6М5 Ion Energy : 3,204384E-16 Средний пробег ионов: 2,32613035597026E-8 Страгглинг среднего пробега ионов: 6,79506169419965E-9 Средний проецированный пробег ионов: 8,38895746733611E-9 Страгглинг среднего проецированного пробега ионов: 2,45057132736608E-9 Максимальная концентрация внедрённой примеси: 1,30236551593508E29 Максимальная концентрация вакансий: 4,42091861648541E29 Максимальное значение остаточных концентрационных напряжений: -367938963,822719 Ion Energy : 7,209864E-16 Средний пробег ионов: 5,078510843904E-8 Страгглинг среднего пробега ионов: 1,48352797212844E-8 Средний проецированный пробег ионов: 1,83151435849541E-8 Страгглинг среднего проецированного пробега ионов: 5,35019588556022E-9 Максимальная концентрация внедрённой примеси: 5,9652761494482E28 Максимальная концентрация вакансий: 9,08301934476326E28 Максимальное значение остаточных концентрационных напряжений: -185484054,22526 Ion Energy : 1,1215344E-15 Средний пробег ионов: 7,04012176741875E-8 Страгглинг среднего пробега ионов: 2,05655119978581E-8 Средний проецированный пробег ионов: 2,53894980219664E-8 Страгглинг среднего проецированного пробега ионов: 7,41674708819403E-9 Максимальная концентрация внедрённой примеси: 4,30315278807487E28 Максимальная концентрация вакансий: 4,09627015317492E28 Максимальное значение остаточных концентрационных напряжений: -137531263,764993 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


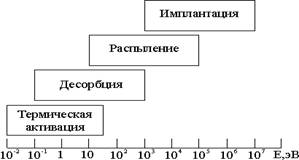
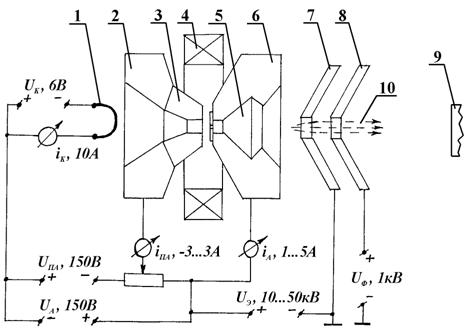
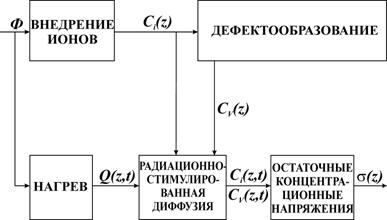
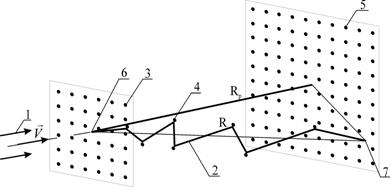
 , (2.1)
, (2.1) число атомов в единице объема (ρ – плотность материала подложки,
число атомов в единице объема (ρ – плотность материала подложки, 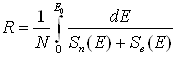 , (2.2)
, (2.2)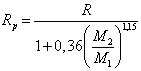 , (2.3)
, (2.3)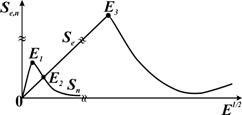
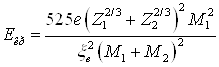 , (2.4)
, (2.4)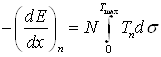 , (2.5)
, (2.5)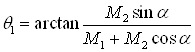 ,
, 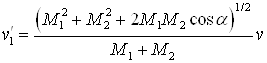 ,
, 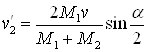 . (2.7)
. (2.7)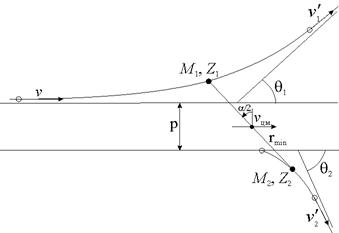
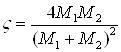 Дж, определяет
максимально возможную энергию, передаваемую при лобовом столкновении (когда
частицы сближаются и удаляются по одной оси):
Дж, определяет
максимально возможную энергию, передаваемую при лобовом столкновении (когда
частицы сближаются и удаляются по одной оси):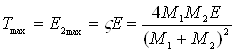 . (2.9)
. (2.9)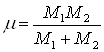 - приведенная масса, кг;
- приведенная масса, кг; 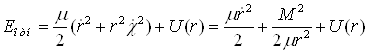 . (2.12)
. (2.12)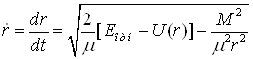 . (2.13)
. (2.13)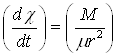 , (2.14)
, (2.14) , (2.15)
, (2.15)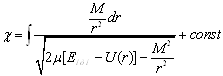 . (2.16)
. (2.16)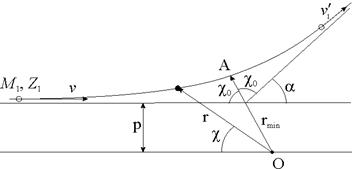
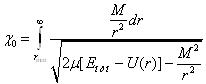 . (2.18)
. (2.18)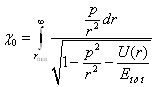 , (2.20)
, (2.20)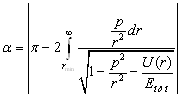 . (2.21)
. (2.21) . (2.22)
. (2.22) . (2.26)
. (2.26)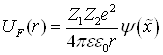 , (2.27)
, (2.27) ;
;
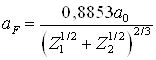 - радиус экранирования
Томаса-Ферми-Фирсова, м [22, 57]. Этот потенциал более приближен к
реальному, особенно для атомов с большим порядковым номером Z. Именно поэтому он наиболее подходит
для расчётов пробегов ионов азота в металлах и сплавах.
- радиус экранирования
Томаса-Ферми-Фирсова, м [22, 57]. Этот потенциал более приближен к
реальному, особенно для атомов с большим порядковым номером Z. Именно поэтому он наиболее подходит
для расчётов пробегов ионов азота в металлах и сплавах.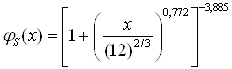 ; (2.28)
; (2.28)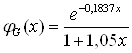 ; (2.29)
; (2.29)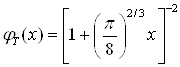 ; (2.30)
; (2.30)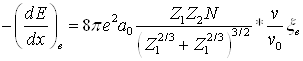 , (2.32)
, (2.32)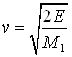 — скорость иона до столкновения,
— скорость иона до столкновения, 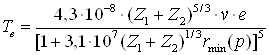 , (2.33)
, (2.33) , (2.34)
, (2.34)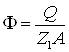 , (2.35)
, (2.35)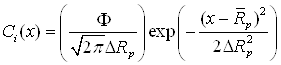 , (2.36)
, (2.36)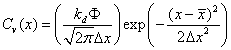 , (2.37)
, (2.37)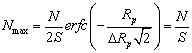 , (2.38)
, (2.38)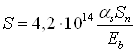 , (2.39)
, (2.39)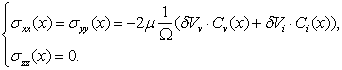 (2.40)
(2.40)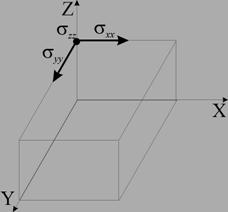
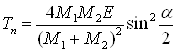 . (3.2)
. (3.2)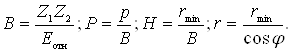 (3.3)
(3.3)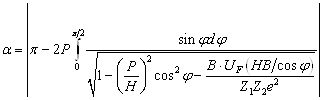 , (3.4)
, (3.4)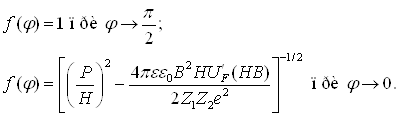 (3.5)
(3.5) , (3.6)
, (3.6) .
.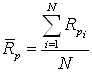 , (3.8)
, (3.8)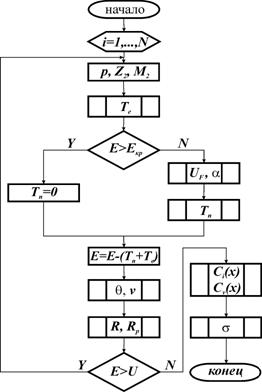
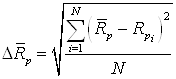 , (3.9)
, (3.9)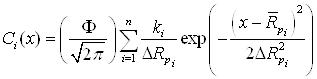 , (3.11)
, (3.11)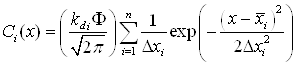 , (3.12)
, (3.12)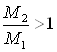 , происходит
сильное рассеяние первичного пучка ионов при внедрении в материал подложки и
получается большой разброс пробегов по величине.
, происходит
сильное рассеяние первичного пучка ионов при внедрении в материал подложки и
получается большой разброс пробегов по величине.