|
Курсовая работа: Термодинамика необратимых процессов и проблем экологииКурсовая работа: Термодинамика необратимых процессов и проблем экологииФедеральное агентство образования ПГПУ им. Белинского Физико-математический факультет Кафедра общей физики Курсовая работа "Термодинамика необратимых процессов и проблем экологии" Подготовила: студентка гр. М-42 Отпущенникова Людмила Проверила: доцент Ляпина Т.В. Пенза 2007 Содержание Введение 1. Основные понятия 2. Первое начало термодинамики 3. Энтропия и вероятность 4. Энтропия и приведенная теплота 5. Второе начало термодинамики 6. Обратимые и необратимые процессы 7. О тепловой смерти мира 8. Термодинамическая шкала температур. Третье начало термодинамики. Недостижимость абсолютного нуля 9. Необходимые и достаточные условия существования систем 10. Энтропия Земли 11. Энтропия и критерий технического прогресса Библиография ВведениеТермодинамика изучает закономерности теплового движения в равновесных системах и при переходе систем в равновесие (классическая или равновесная, термодинамическая), а так же обобщает эти закономерности на неравновесные системы равновесная термодинамическая или термодинамика необратимых процессов. Термодинамика необратимых процессов является сравнительно молодым и интенсивно развивающимся разделом термодинамической физики. Она возникла в результате обобщения классической термодинамики на область малых отклонений системы от равновесия и в дальнейшем была распространена на построение теории процессов в сильно неравновесных системах. Прежде чем перейти к изложению основных законов и методов термодинамики и изучения свойств различных систем, раскроем содержание главных термодинамических понятий. 1. Основные понятияМакроскопическая система - всякий материальный объект, всякое тело, состоящее из большого числа частиц. Равновесное состояние системы - это такое состояние, когда в системе не только все параметры постоянны во времени, и нет никаких стационарных потоков за счет действия каких-либо внешних источников. Изолированная или замкнутая система - система, которая не обменивается с окружающими телами ни энергией, ни веществом. Открытая система - система, которая обменивается с окружающими телами энергией и веществом. Закрытая система - система, не обменивающаяся с другими телами веществом, но обменивающаяся энергией. Энергия системы - энергия непрерывно движущихся и взаимодействующих частиц. Полная энергия системы разделяется на внешнюю и внутреннюю. Часть энергии, состоящая из энергии движения системы как целого и потенциальной энергии системы в поле внешних сил, называется внешней энергией. Остальная часть энергии системы называется внутренней энергией. Количество теплоты - энергия, переданная системе без изменения её внешних параметров. Процесс называется равновесным или квазистатическим, если все параметры системы изменяются физически бесконечно медленно, так что система все время находится в равновесных состояниях. Время релаксации - промежуток времени, в течении которого система возвращается в состояние равновесия. Если изменение какого-либо параметра a
происходит за время t, меньшее или равное времени
релаксации τ (t≤τ), так что Процесс перехода системы из состояния 1 в 2 называется обратимым, если возвращение этой системы в исходное состояние из 2 в 1 можно осуществить без каких бы то ни было изменений в окружающих внешних телах. Процесс же перехода системы из состояния 1 в 2 называется необратимым, если обратный переход системы из 2 в 1 нельзя осуществить без изменений в окружающих телах. 2. Первое начало термодинамикиТермодинамика - дедуктивная наука. Её основные успехи могут быть охарактеризованы тем, что она позволяет получить множество различных соотношений межу величинами, определяющими состояние тел, опираясь на весьма общие электрические законы - начала-термодинамики. Обсудим содержание этих основных законов и соответствующим им основных уравнений термодинамики. Одной из аксиом термодинамики является первое начало термодинамики, утверждающее следующее: внутренняя энергия термодинамической системы является функцией состояния, изменяющейся только при взаимодействии с окружением. Изменение внутренней энергии связано с работой и количеством теплоты уравнением первого начала термодинамики: δQ = dE + δА. (1) Выражение (1) по существу является законом сохранения энергии, описывающим взаимодействие макросистемы с окружением. Первое начало термодинамики, устанавливая связь между dE, δА и δQ, тем самым позволяет свести измерение dE к измерению макроскопических величин, таких как работа или количество теплоты. С другой стороны, первое начало термодинамики позволяет сделать определенный вывод о той механической работе, которую можно получить в том или ином процессе, что представляет большой практический интерес. Исторически установление первого начала термодинамики (закона сохранения энергии) было связано как раз с неудачами при попытках сконструировать машину, которая совершала бы работу, не затрачивая при этом никакой энергии и не получая теплоты извне. В термодинамике такую неосуществимую машину называют вечным двигателем первого рода. Для периодически действующей машины dE = 0; поэтому для периодического производства ею работы в силу закона сохранения энергии необходимо или подводить количество теплоты δQ или использовать работу δА других источников энергии. Невозможно построить вечный двигатель, который производил бы большую работу, чем количество поглощаемой им извне энергии. Последнее утверждение можно рассматривать как одну из формулировок первого начала термодинамики. В дальнейшем для обозначения элементарного изменения внутренней энергии dE, элементарной работы δА и количества теплоты δQ будем использовать только один символ: d. 3. Энтропия и вероятностьПонять энтропию - это знать ее происхождение, знать связь ее с другими понятиями, уметь применять энтропию на практике. Чем больше связей знают читатели между энтропией и другими понятиями, тем лучше они усваивают, что такое энтропия. В приборе Гей-Люссака в одном шаре находится газ (при малой его плотности). Другой шар эвакуирован. Открывают кран на трубке, соединяющей оба шара. Результат опыта известен: газ равномерно заполняет оба шара. Температура всего газа та же, что и до расширения. При самопроизвольном изотермическом расширении газа увеличивается его энтропия (процесс адиабатический, и энтропия источников теплоты не изменяется). Самопроизвольное сжатие газа в приборе Гей-Люссака до прежнего объема исключено: энтропия уменьшилась бы. Газ состоит из молекул (некоторые газы состоят из атомов). В газе малой плотности одна молекула воздействует на другую только в короткие моменты столкновений между молекулами. Большую же часть времени молекула свободно двигается по объему, предоставленному всему газу. Предположим, что физик может отличить одну молекулу от других. Физика спрашивают, в каком шаре находится выбранная молекула, подчеркнутая красным, как говорил Эйнштейн. (Объемы шаров, чтобы упростить рассуждения, равны) Физик ответит: до наблюдения не знаю. Он сошлется на то, что на выбранную молекулу (как и на все остальные) ничего не воздействует. Выбранная молекула (как и все остальные) никак не предпочитает один шар другому. Объемы шаров равны. Поэтому и физик не может предпочесть один шар другому. На техническом языке, вероятность нахождения выбранной молекулы в любом из шаров равна половине. Сумма вероятностей равна единице (половина плюс половина), равна достоверности. В каком-нибудь из двух шаров выбранная молекула обязательно находится. Физику дальше ставят как будто совсем неразрешимый вопрос: в каком из шаров находятся все молекулы газа? На вопрос, где находится одна выбранная молекула, физик не мог ответить. Где же ему ответить на второй вопрос?! Ведь при О °С и 1 атм в 1 см3 газа находится 2,7x1019 молекул. [Для сопоставления: пять миллиардов лет (возраст Земли) - 1,6х1017 секунд.] Физик, однако, с полной уверенностью ответит: ни в одном из шаров не содержатся все молекулы газа. Молекулы газа равномерно распределены между обоими шарами. Во всяком случае, отклонение от равномерного распределения при значительном объеме шаров, значит, и при большом числе молекул крайне мало, и этим отклонением можно спокойно пренебречь. Откуда такая уверенность? Из подсчета вероятностей. Именно потому, что для каждой молекулы вероятность находиться в том или другом шаре равна половине, все молекулы не могут находиться в одном только шаре. Вероятность такого случая тем меньше, чем больше число молекул. При том числе молекул, с каким обычно имеют дело в термодинамике, вероятность скопления всех молекул в одном только шаре чрезвычайно мала. Выдающийся французский математик Э. Борель (1871-1956) писал: "Я пришел к выводу, что не следует бояться применить слово достоверность для обозначения вероятности, которая отличается от единицы на достаточно малую величину". Статистический закон для большого числа молекул пробил себе дорогу через случайности для отдельной молекулы. Приведенный пример свидетельствует, что существует связь между возрастанием энтропии в опыте Гей-Люссака и вероятностью распределения газа между обоими шарами. Обобщая, можно сказать: при самопроизвольном процессе система переходит из менее вероятного состояния в более вероятное. 4. Энтропия и приведенная теплотаПервое начало термодинамики позволяет определить, возможен ли с энергетической точки зрения тот или иной процесс в замкнутой системе. Но оно ничего не говорит о возможных направлениях процессов (в частности самопроизвольных). Так, например, первый закон не запрещает самопроизвольного перехода теплоты от холодного тела к горячему, либо концентрирования газа в малой части сосуда и снижения давления в остальной части сосуда. Но, как известно, в природе такие процессы не наблюдаются. Для суждения о возможном направлении процессов в термодинамике вводится еще одна функция состояния - энтропия. Так как энтропия является функцией состояния макросистемы, то внутренняя энергия может рассматриваться как функция энтропии и, в простейшем случае, одного внешнего параметра, например V. Тогда
При равновесных процессах
Сравнивая выражения (2) и (3), нетрудно установить тождественность этих соотношений при условии выполнения равенств:
Из равенства (4) видно, что для обратимых процессов
Так как dS является
полным дифференциалом, то и величина Зная элементарное изменение энтропии dS, можно без труда найти и конечное изменение этой величины для любого обратимого процесса. Именно:
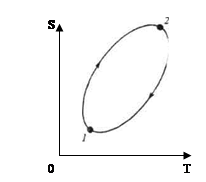
(рис. 1) Если обратимый процесс характеризуется замкнутым циклом, то очевидно изменение энтропии и контурный интеграл от приведенной теплоты в этом случае равны нулю (рис.1):
Для адиабатного обратимого процесса приведенная теплота
равна нулю, а энтропия остается постоянной. Однако если процесс протекает
необратимо, то энтропия, как было выяснено ранее, возрастает, т.е. для
адиабатного необратимого процесса Изменение энтропии при необратимых адиабатных процессах
наводит на мысль использовать эту величину для характеристики необратимости
любых процессов в макросистемах. Причем за меру необратимости удобно принять
разность между dS и Используя это соображение, можно утверждать, что все процессы в макросистемах протекают таким образом, что
Если процесс круговой, то
причем знак неравенства относится к неравновесным процессам, а равенство характеризует равновесные процессы. Таким образом, энтропия действительно является такой функцией состояния, применение которой позволяет определить направленность протекания реальных процессов в макросистемах. Второе начало термодинамики выражает это утверждение в форме постулата. 5. Второе начало термодинамикиВторое начало термодинамики - один из принципов термодинамики, постулирует существование еще одной функции состояния - энтропии и определяет характер ее изменения в обратимых и необратимых процессах, утверждая, что изменение энтропии в макросистемах больше или равно изменению приведенной теплоты для неравновесных и равновесных процессов соответственно. Математическим выражением второго начала термодинамики является соотношение между элементарным изменением энтропии и приведенной теплотой:
Воспользуемся первым началом термодинамики и выразим в выражении (12) количество теплоты dQ через изменение внутренней энергии dE и элементарную работу dA. Получим:
Знак равенства в выражении (13) соответствует обратимым процессам, неравенство характеризует изменение энтропии в неравновесных процессах. Таким образом, для равновесных процессов из выражения (13) имеем равенство: TdS = dE + dA, (14) называемое основным уравнением термодинамики для равновесных процессов, и неравенство: TdS>dE + dA, (15) называемое основным неравенством термодинамики для неравновесных процессов. Процессы в макросистемах могут протекать только при условии выполнения соотношений (12). Существует несколько эквивалентных формулировок второго начала термодинамики, они отражают исторический ход развития знаний в этой области и подчеркивают различные стороны проблемы. Формулировка Клаузиуса (1850): процесс, при котором в системе не происходит никаких изменений, кроме передачи теплоты от горячего тела к холодному, является необратимым; иначе говоря, теплота не может самопроизвольно перейти от более холодного тела к более горячему без каких-либо других изменений в системе. Формулировка Томсона (Кельвина) (1851): процесс, при котором теплота переходит в работу, является необратимым; иначе говоря, невозможно преобразовать в работу всю теплоту, взятую от тела с однородной температурой, не производя никаких других изменений в состоянии системы. Принцип невозможности создания вечного двигателя второго рода: невозможно создать периодически работающую машину, которая производила бы работу за счет поглощения теплоты одного теплового резервуара, не вызывая при этом никаких других изменений состояния системы. (Такую воображаемую машину принято называть вечным двигателем второго рода) 6. Обратимые и необратимые процессыПо второму началу термодинамики в природе возможны процессы, при которых превращение теплоты в работу связано с компенсацией, и невозможны процессы, при которых такое превращение не сопровождается компенсацией. Это приводит к делению всех процессов в замкнутой системе на обратимые и необратимые. Процесс перехода системы из состояния 1 в 2 называется обратимым, если возвращение этой системы в исходное состояние из 2 в 1 можно осуществить без каких бы то ни было изменений в окружающих внешних телах. Процесс же перехода системы из состояния 1 в 2 называется необратимым, если обратный переход системы из 2 в нельзя осуществить без изменений в окружающих телах. Очевидно, что всякий квазистатический процесс является обратимым. Действительно, при квазистатическом процессе состояние системы в каждый момент полностью определяется внешними параметрами и температурой, поэтому при равновесных изменениях этих параметров в обратном порядке система также в обратном порядке пройдет все состояния и придет в начальное состояние, не вызвав никакого изменения в окружающих телах. При процессах с трением, как мы отмечали, работа может быть без компенсации превращена в теплоту; так как обратный переход системы из конечного состояния в начальное связан с переходом теплоты в работу, а это невозможно осуществить без изменения в окружающих телах, то, следовательно, процессы с трением необратимы. А так как всякий равновесный процесс обратим, то необратимый процесс с трением неравновесен. Мерой необратимости процесса в замкнутой системе является изменение новой функции состояния - энтропии, существование которой у равновесной системы устанавливает первое положение второго начала о невозможности вечного двигателя второго рода. Однозначность этой функции состояния приводит к тому, что всякий необратимый процесс является неравновесным. Верно и обратное заключение: всякий неравновесный процесс необратим, если в дополнение ко второму началу осуществляется достижимость любого состояния неравновесно, когда оно достижимо из данного равновесно [вся современная практика подтверждает выполнение этого условия; однако противоположное условие выполняется не всегда]. Деление процессов на обратимые и необратимые относится лишь к процессам, испытываемым изолированной системой в целом; разделение же процессов на равновесные и неравновесные с этим не связано. В качестве примеров необратимых процессов приведем следующие: 1. Процесс теплопередачи при конечной разности температур, необратим, так как обратный переход связан с отнятием определенного количества теплоты у холодного тела, превращением его без компенсации (некомпенсировано) в работу и затратой ее на увеличение энергии нагретого тела. Необратимость этого процесса видна также из того, что он не статичен. 2. Расширение газа в пустоту необратимо, так как при таком расширении не совершается работа, а сжать газ так, чтобы не совершить работу, нельзя. Произведенная же при сжатии работа идет на нагревание газа. Чтобы газ не нагревался, нужно отнять у него теплоту и превратить ее в работу, что невозможно без компенсации. 3. Процесс диффузии необратим. Действительно, если в сосуде с двумя различными газами, разделенными перегородкой, снять перегородку, то каждый газ будет диффундировать в другой. Для разделения газов каждый из них нужно сжимать. Чтобы они не нагревались, необходимо отнять у них теплоту и превратить ее в работу, что невозможно без изменения в окружающих телах. 7. О тепловой смерти мираПостепенно все горячие тела будут отдавать энергию более холодным. Энтропия будет возрастать. Наконец, все температуры уравниваются. Энтропия достигнет максимума, что будет соответствовать полному хаосу. В мире останется только энергия беспорядочного движения молекул. Никакое упорядоченное механическое движение тогда не может быть получено. Все процессы прекратятся. Наступит тепловая смерть мира. Эта проблема серьезно волновала ученых в конце XIX в. Однако, во-первых, всю вселенную нельзя считать замкнутой системой, а наши рассуждения относятся только к таким системам. Во-вторых, уже говорилось о том, что переход от полного беспорядка к порядку очень маловероятен. Поэтому применяется второе начало термодинамики ко всей Вселенной и необозримо большим промежуткам времени не следует. 8. Термодинамическая шкала температур. Третье начало термодинамики. Недостижимость абсолютного нуляВторое начало термодинамики можно использовать для построения термодинамической шкалы температур. Так как КПД цикла Карно не зависит от рабочего тела, то можно вообразить такую процедуру. Некоторое стандартное тело в определенном состоянии (например, вода, кипящая при атмосферном давлении) выбирается в качестве нагревателя. Другое стандартное тело (например, лед, тающий при атмосферном давлении) выбирается в качестве холодильника. Разность температур Тн и Гх (сами температуры пока неизвестны) делится на произвольное число частей, чем устанавливается размер градуса (скажем, на сто частей). Осуществляется обратимый цикл Карно с каким-либо веществом. Измеряется количество теплоты Q1, заимствованной от нагревателя, и количество теплоты Q2, отданной холодильнику:
Имея, кроме того, условие: TH-TX=100°С, получаем два уравнения, определяющие Tн и Тх. Если теперь взять некое вещество при неизвестной температуре Т и использовать его в качестве нагревателя при прежнем холодильнике (температура Tх), то, проводя цикл Карно и измеряя Q1’ и Q2’, можно написать:
Отсюда находится искомая температура Т. Построенная таким образом шкала температур, как выяснилось, совпадает со шкалой, получаемой при измерениях с газовым термометром. Из уравнения (15) следует, что нулем температуры является температура, при которой количество теплоты Q2 равно нулю. В этом случае КПД цикла Карно должен равняться единице. Так как большим он стать не может (по первому началу), то эта температура наинизшая. Термодинамическая шкала совпадает со шкалой газового термометра, значит, совпадают и их нулевые точки. Напомним, что абсолютным нулем является температура t= - 273,15 °С. Согласно второму началу невозможно получить КПД тепловой машины, равный единице, поэтому можно дать еще одну формулировку второго начала, подчеркивающую это обстоятельство: абсолютный нуль температуры принципиально недостижим, хотя к нему можно приблизиться сколь угодно близко. В настоящее время уже получена температура, составляющая всего 10-6 К. Так как энергия беспорядочного движения частиц газа пропорциональна температуре, то следует ожидать, что при абсолютном нуле беспорядочное движение должно прекратиться - частицы будут располагаться наиболее упорядоченным образом (но, конечно, будут иметь место внутримолекулярные или внутриатомные движения). Этой наибольшей упорядоченности расположения частиц должна отвечать наименьшая энтропия. В. Нернст (1864 - 1941), основываясь на ряде физико-химических наблюдений, высказал положение, часто называемое третьим началом термодинамики: энтропия любой макросистемы при стремлении ее температуры к абсолютному нулю стремится к одному и тому же для всех систем постоянному значению, которое можно принять равным нулю. В заключение отмечу, что область приложения термодинамики не ограничивается только тепловыми процессами. Изменения внутренней энергии за счет химических процессов, процессов горения, внутриатомных превращений и многих других (включая и процессы, происходящие в живых организмах) также успешно исследуются термодинамикой. Однако сложность подобных исследований не позволяет изучать их в общем курсе физики. 9. Необходимые и достаточные условия существования системРождение жизни на Земле, ее развитие и существование, антропогенная деятельность находятся в строгом соответствии со вторым началом термодинамики - законом возрастания энтропии. Этот закон показывает, как и каким образом происходит неизбежное ухудшение качества окружающей среды для достижения главной цели - обеспечения существования жизни на планете и устойчивого развития. Для эволюции упорядоченных систем и их существования требуются необходимые и достаточные условия: необходимы источники, снабжающие системы веществом, энергией с низкой энтропией; возможность избавления от отходов, обладающих высокой энтропией. Особенность живого организма состоит в том, что он поддерживает себя на сравнительно низком уровне энтропии, пользуясь высококачественной энергией, за счет возрастания энтропии окружающей среды, а условием существования жизни является достаточность энтропийных запасов окружающей природной среды. Для обеспечения жизни окружающая среда должна находиться в "достаточном упорядоченном состоянии". В ней должны находиться ряд питающих подсистем: солнечное излучение, воздух, вода, минералы, растения, животные и т.п. Существование и развитие жизни создают новые высокоупорядоченные системы, но при этом ускоряются процессы возрастания энтропии. В окружающую среду (в космос) выносятся низкокачественные потоки энергии (длинноволновые излучения) и другие отходы человеческой цивилизации. Жизнь создает актуальную упорядоченность из неактуальной неупорядоченности. При этом происходит увеличение энтропии в неактуальной части общей системы. В нашем случае актуальной подсистемой является биосфера на Земле, неактуальной - космическое пространство, откуда приходит солнечное излучение, дающее жизнь на Земле. Туда же, в космическое пространство, рассеивается излучение с земной поверхности. Это излучение обладает большей энтропией, т.е. более низким качеством энергии, чем поток солнечного излучения. Поэтому рост упорядоченности в биосфере Земли с большим избытком оплачен увеличением энтропии Вселенной. Главное при этом заключается в том, что происходит перемещение роста энтропии в неактуальные части системы. Таким образом, в полном согласии с законом возрастания энтропии достигается локальное уменьшение энтропии в актуальных для жизни человека подсистемах. В действительности, нет ни одного процесса в жизни, где нарушался бы закон возрастания энтропии. Все процессы в биосфере связаны с этим законом. Человек, как высший продукт живой природы, находится на верхнем уровне энтропийной пирамиды, где ее значение имеет очень малое значение, но устойчивость этого уровня обеспечивается за счет значительного возрастания энтропии нижележащих уровней и других питающих подсистем. Положение уровня человека весьма чувствительно к любым внешним воздействиям и требуется большой набор дополнительных достаточных условий, обеспечивающих относительную стабильность существования этого уровня, сложившегося в ходе длительных процессов эволюции живой материи. Мало того, что для обеспечения человеческой жизни нужны воздух, вода, пища, жилище, солнечное излучение и многое другое, но требуется, чтобы вода и воздух были чистыми. Такие, к каким привык человек за долгие годы эволюционного развития. Требуется большой набор биотических и абиотических факторов, обеспечивающих достаточность устойчивости жизни. Быстрое изменение одного из этих факторов может нарушить устойчивость уровня в пирамиде, где находится человек. Ни состав воды, ни состав воздуха и т.д. не должны быстро меняться от состава, сложившегося за эволюционный период. Если, например, абиотические факторы меняются (состав воды, воздуха и т.п.), то скорость этих изменений должна быть такой, чтобы успевал срабатывать механизм адаптации живого организма. Необходимые (обязательное наличие низкой энтропии открытой подсистемы за счет большего прироста энтропии внешних питающих систем) и достаточные (набор биотических и абиотических факторов, постоянных или меняющихся со скоростью адаптации) условия обеспечивают устойчивость жизни в биосфере. Необходимо отметить, что эти условия не охватывают все стороны многогранной жизни человека и общества с его наукой, культурой, производством, искусством, этикой, моралью и т.д., однако они являются фундаментом и каркасом здания, в котором живет и творит человек. 10. Энтропия ЗемлиПланета Земля вместе с живой и неживой природой представляет собой сложнейшую самостоятельную экосистему, в которой нужно заботиться о ее состоянии, способном обеспечить существование жизни. Для этого необходимо, чтобы имелись, во-первых, источники, в которых будет происходить возрастание энтропии в системе "Земля - космос" за счет уменьшения энтропии в ноосфере, во-вторых, необходимы способы избавления от отходов человеческой цивилизации. Важнейшим источником энергии с низким значением энтропии является солнечное излучение, которое обеспечивает жизнедеятельность биосферы, протекание различных неравновесных процессов, включая фотосинтез и другие биохимические и биофизические реакции. Длинноволновое тепловое излучение Земли, уходящее в космос, уносит часть "отходов" в виде приращения энтропии, как неизбежного побочного продукта многих земных процессов естественного и техногенного происхождения. Баланс энергии при этом сохраняется. Главное заключается в том, что солнечная энергия обладает более низкой энтропией (следовательно, более высоким качеством энергии), чем уходящее в космос длинноволновое излучение Земли, обладающее более высокой энтропией (следовательно, более низким качеством энергии). Иными словами, Земля получает от Солнца качественную энергию с низкой энтропией, а отдает в космос некачественное излучение с высокой энтропией и, таким образом, "очищается" от избытка энтропии. Последний процесс также важен, как и первый процесс получения качественного солнечного излучения. Эти две стороны пока не вызывают беспокойства: солнечного излучения хватит на миллионы лет, а приращение энтропии во Вселенной за счет поступления избытков энтропии от антропогенной деятельности ничтожно мало. Вопрос в другом. В результате научно-технической революции и научно-технического прогресса нарушается устойчивое равновесие системы "человек - среда". В настоящее время настолько много различных видов загрязнений биосферы, что требуются специальные дополнительные меры для их утилизации. Но с другой стороны, для их утилизации требуется энергия и средства. Это вызывает приращение энтропии в других областях, которые поставляют эту энергию и средства. Возникает заколдованный круг, одно место очищают, передвигая отходы в другое место, аналогично тому, что дымовая труба строится выше с тем, чтобы продукты выхлопа уносились по возможности дальше, в соседнюю область. Если рассматривать в целом весь Земной шар, то категория "чистое производство", "полная утилизация" при глобальном балансе представляет собой избавление от своих отходов за счет увеличения их суммарного количества на планете. Для выхода из этого порочного круга можно рассмотреть два пути: лучше и эффективнее использовать солнечное излучение; найти и ввести новые источники энергии с низкой энтропией. По первому способу возможно в недалеком будущем в космосе создать приемники солнечного излучения в виде совершенных гелиобатарей и передавать эту энергию на Землю. По второму способу можно использовать атомную или термоядерную энергию. При этом имеем низкую энтропию процессов высвобождения энергии при превращении атомных ядер. Однако, при всё увеличивающемся росте энергопотребления (например, в 102 раз больше, чем в настоящее время) снова встанет проблема захоронения радиоактивных отходов в огромных количествах и избавления от тепловых загрязнений. Бросовое тепло от атомных станций и других источников энергии вызовет существенный нагрев атмосферы, гидросферы, литосферы, что является серьезной угрозой, нарушающей устойчивое равновесие. Оценим величину энтропии, применительно к тепловой системе "Земля". Считаем, что падающее солнечное излучение имеет внутреннюю энергию Е1 и температуру Т2 а рассеянное Землей в космос излучение имеет соответственно Е2 и Т2. В среднем энергия на Земле не накапливается, поэтому с известным приближением можно считать, что Е1=Е2 = Е и энтропия на Земле равна разности энтропии падающего солнечного излучения и рассеянного в космос излучения Земли. Считаем Землю равновесной термодинамической системой типа абсолютно черного тела. Величина энтропии Земли по абсолютной величине будет равна [3, 4]:
Считая T2 ≈6000 К и T2 ≈300 К, с учетом интенсивности солнечного излучения и геометрических размеров Земли, имеем:
Учитывая, что
Из (18) видно, что чем меньше Т2 т.е. более глубокое охлаждение уходящего излучения от Земли в космос при постоянных количестве и качестве солнечного излучения, тем можно больше добиться большей разности энтропии между качественной солнечной энергией и низкокачественной, рассеянной в космос энергией Земли. При большей деградации энергии Е2 Земли, рассеиваемой в космос в виде более длинноволнового излучения, большее число фотонов будет переносить заданное количества энергии, так как солнечное излучение, падающее с энергией Е1 и частотой v1 имеет N1 квантов, а уходящее в космос с поверхности Земли излучение с энергией Е2 имеет N2 квантов. Учитывая, что E1 = E2 и v1>v2, имеем: N1hv1 = N2hv2 (19) или Увеличение числа квантов N2 с частотой v2<v1 обозначает рост энтропии. Растительный покров Земли дополнительно способствует охлаждению уходящего излучения, т.е. температура Т2 уменьшается, но при этом увеличивается рост энтропии Вселенной. Снова приходим к начальному толкованию. Локально в отдельной упорядоченной подсистеме можно добиться уменьшения энтропии, но для всей системы в целом будет большее пиращение энтропии. Для отдельных термодинамических систем важнейшей характеристикой является производная энтропии по времени: dSi/dt, где Si - внутренняя энтропия системы. Через эту величину можно выражать условия динамического равновесия, эволюционного развития и устойчивого равновесия. В ходе различных производственных процессов, использования природных ресурсов, распыления материалов в окружающей среде, образования в виде физических, химических и биологических загрязнений энтропия системы "человек - окружающая среда" увеличивается. 11. Энтропия и критерий технического прогрессаВведем понятие энтропии, под которым будем понимать энтропию с обратным знаком, чтобы привести в соответствие повышение качества энергии с ростом негэнтропии. Энтропия же при этом уменьшается с повышением качества энергии. Одним из объективных факторов оценки развитого общества является потребление энергии на душу населения. Воспользуемся общим подходом, развитом в [3, 4] и связывающим неэнтропию с критерием технического прогресса. Считаем, что за время Δt обществом использовано ΔЕ1 энергии. Введем критерий К1 который оценивает энергопотребление общества за период Δt:
Естественно, что критерий K1 (t) характеризует развитие общества только по одному критерию - энергопотреблению. В развитом обществе коэффициент полезного действия ŋ1 (t)) при использовании энергии будет выше. Тогда критерий технического прогресса K (t) запишем в виде:
С учетом состояния имеющихся в окружающей природной среде источников энергии E2 (t) за этот период критерий технического прогресса запишем в виде:
Учитывая актуальность использования энергии в важных,
общественно полезных сферах жизнедеятельности, необходимо ввести еще один
коэффициент - "социально-полезный" КПД
Затем в выражении (24), заменив энергию на негэнтропию, получаем:
где Безусловно, критерий технического прогресса К5 (t) можно уточнять, учитывая различные факторы жизнедеятельности. Однако из (25) видны степени технического уровня, истощение природных ресурсов и загрязнения окружающей природы среды. Расход негэнтропии При этом можно допустить скачкообразный рост негэнтропии Библиография1. Базаров И.П. термодинамика: учеб. для. вузов. - 4-е изд., перераб. и доп. - М.: Высш. Шк., 1991. - 376 с.: ил. 2. Бордовский Г.А., Бурсиан Э.В. Б.82. общая физика: курс лекций с компъютерной поддержкой: Учеб. пособие для студ. Высш. Учеб. заведений: В 2 Т. - М: Издательство Владос-пресс, 2001. - Т.1. - 240с.: ил. 3. Гершензон Е.М. и др. Г37 Молекулярная физика: учеб. пособие для студ. Высш. Пед. Учеб. заведений /Е.М. Гершензон, И.Н. Малов, А.М. Мансуров. - М.: Издательский центр "Академия", 2000. - 272 с. 4. Кричевский И.Р., Петрянов И.В. К828 Термодинамика для многих. М., "Педагогика", 1975., 160с с ил. (библиотечка Детской энциклопедии "Ученые - школьнику") 5. Куклев Ю.И. к.89. Физическая экология: Учеб. пособие. - М.: Высшая школа, 2001. - 357 с.: ил. |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


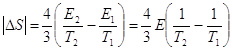 (16)
(16)