|
Реферат: Адсорбция и адсобционные равновесияРеферат: Адсорбция и адсобционные равновесияАдсорбция на границе раздела "твердое тело- газ". Классификация пористых тел по Дубинину. Капиллярная конденсация. Уравнение Томсона (Кельвина). Капиллярно-конденсационный гистерезис. Теория объемного заполнения пор. Теория Поляни
Адсорбция - процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы. Адсорбция может наблюдаться в многокомпонентных системах и при перераспределении в поверхностный слой уходит тот компонент, который сильнее понижает поверхностное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры - уплотнение, которое называется автоадсорбцией. В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению, но и за счет химической реакции компонентов с поверхностью вещества. В этом случае поверхностная энергия может даже увеличиваться на фоне снижения энергии всей системы. Вещество, на поверхности которого происходит адсорбция, называется адсорбентом, а вещество, которое перераспределяется – адсорбатом. Обратный процесс перехода вещества с поверхности в объем фазы - десорбция. В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело жидкость, жидкость - жидкость, жидкость - газ. Для количественного описания адсорбции применяют две величины: первая измеряется числом молей или граммами, приходящимися на единицу поверхности или массы адсорбента: А = m1/m2 - абсолютная адсорбция, А = ni/S. Величина, определяемая избытком вещества в поверхностном слое, также отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или относительной адсорбцией (Г).
Адсорбция зависит от концентрации компонентов и температуры. А = f(c,T)- жидкость; А = f(P,T)- газ Различают следующие виды зависимостей:
Поскольку в качестве твердых адсорбентов используют пористые тела, рассмотрим некоторые методы получения твердых тел. Основных методов два. 1. Первый метод заключается в синтезе гидрозоля, который затем подвергают коагуляции до получения геля. Гель высушивают, частицы в результате этих операций срастаются с образованием твердого каркаса. Так как частицы золя высокодисперсны, то пористый материал получается с большой удельной поверхностью. Для удобства использования комки дробят, таблетируют, гранулируют. Обычно размер зерен адсорбента имеет предел от 0.1 до 7 микрон. Таким образом получают силикагель и другие адсорбенты. 2. Второй метод заключается в обработке крупнопористых материалов агрессивными газами или жидкостями. При такой обработке образуется губчатая структура. Этим методом получают активированный уголь из природных материалов, из которых сначала удаляют летучие вещества при нагревании без доступа воздуха. В результате образуется крупнопористая структура. Затем активируют уголь путем окисления газом кислорода или СО2, или водяным паром. Таким же образом получают никель Рэнея, т.е. берут сплав никеля и алюминия и его высушивают. По классификации М.М. Дубинина за основу принят размер пор и механизм протекающих на них процессов. 1. Макропористые тела. Радиус пор от 100 - 200 нм, Sуд = 0.5 - 2 м2/г - Для этих же адсорбентов пригодна теория адсорбции Ленгмюра. В адсорбентах и катализаторах макропоры выступают в качестве транспортных каналов и адсорбцией в них можно пренебречь. 2. Переходно-пористые тела. Радиус пор более 2 - 100 нм, Sуд = 100 - 500 м2/г. Для них характерна полимолекулярная адсорбция, которая с увеличением давления заканчивается капиллярной конденсацией. 3. Микропористые тела. Радиус пор 0.5 - 2 нм, Sуд = 500 - 1000 м2/г. Отличительной особенностью этих тел является чрезвычайно близкое расположение противоположных стенок в порах. При этом их поля поверхностных сил перекрываются и они действуют во всем объеме микропор. К ним применима теория объемного заполнения микропор. Реальные и промышленные адсорбенты имеют набор всех пор, но соотношение пор с разными радиусами различно. Каких пор больше, к такому классу их и относят. Как уже отмечалось, влияние структуры пористого тела на адсорбцию заметно проявляется уже на переходно-пористых телах. Это обусловлено проявлением капиллярных сил. Появление этого связано со сродством адсорбата к адсорбенту. Основываясь на закономерностях капиллярных явлений, можно утверждать, что сродство должно быть достаточно для смачивания поверхности твердого тела жидкостью, появляющейся в результате конденсации в порах. Только в случае смачивания адсорбент будет втягивать в поры адсорбат, увеличивая тем самым адсорбцию. Чем меньше размер пор, тем сильнее капиллярное удерживание адсорбата. Если поверхность не смачивается, то наблюдается явление капиллярного выталкивания, адсорбция в этом случае минимальна и возможна только в крупных порах. Адсорбция в переходно-пористых телах происходит по механизму капиллярной конденсации. Капиллярная конденсация начинает проявляться при определенной степени заполнения адсорбента или при определенном давлении пара, характерном для данной системы. К этому моменту поверхностная энергия адсорбции практически полностью скомпенсирована в результате полимолекулярной адсорбции, а макропоры заполнены адсорбатом. В результате повышения давления пара заполняются конденсатом все крупные поры. Размеры радиусов менисков подчиняются уравнению капиллярной конденсации Томсона (Кельвина).
где р - давление пара над искривленным мениском; рs - давление насыщенного пара над плоской поверхностью; s - поверхностное натяжение конденсированной жидкости; r - радиус кривизны мениска.
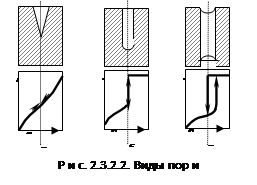
Из уравнения видно, что при смачивании обеспечивается отрицательная кривизна мениска конденсата (вогнутый мениск), конденсация в порах наступает при давлении, которое меньше давления насыщенного пара, т.е. р/рs<1. Капиллярная конденсация не является следствием адсорбционных сил адсорбента и адсорбата в капилляре, но адсорбция является первым этапом капиллярной конденсации, если адсорбционные силы очень велики, а капилляры очень узкие, то конденсация идет до тех пор, пока не будет достигнуто давление насыщения над поверхностью. Для адсорбентов переходной пористости характерна изотерма адсорбции с петлей капиллярно-конденсационного гистерезиса (рис. 2.3.2.1). При малых давлениях, когда конденсация не происходит, гистерезис не наблюдается. Начало его появления зависит от природы адсорбента и адсорбата. Пористые структуры разнообразны, однако считается, что их можно смоделировать тремя видами: 1) конусообразные; 2) цилиндрические с одним открытым концом; 3) цилиндрические с двумя открытыми концами. В реальных адсорбентах имеются все виды пор, которые заполняются при разных давлениях, поэтому реальные изотермы имеют вид, представленный на рис. 2.3.2.2:
В первой группе в конусообразных порах конденсация начинается со дна пор, где кривизна наибольшая. По мере заполнения поры радиус мениска увеличивается (уменьшается кривизна), поэтому для дальнейшего заполнения поры необходимо увеличить давление (рис. 2.3.2.2, а). Процесс десорбции идет в обратном направлении и описывается той же кривой. Во второй группе конденсация также начинается со дна, где кривизна сферическая и поэтому наибольшая (см. рис. 2.3.2.2, б). Так как пора цилиндрическая, то она заполняется целиком при определенном радиусе мениска, что отвечает и определенному давлению пара. Капиллярная конденсация в этих порах также происходит обратимо. В третьей группе (в): конденсация начинается на стенках пор, имеющих кривизну, в 2 раза меньшую сферы того же радиуса. Поэтому заполнение происходит при больших давлениях пара. Конденсация на стенках приводит к уменьшению радиуса пор и ее мгновенному заполнению при давлении, отвечающем началу конденсации. На концах образуются сферические мениски жидкости. Десорбция может начаться при давлении, соответствующем радиусу кривизны этих менисков. Таким образом, опорожнение происходит при меньшем давлении, чем ее заполнение. Это и объясняет наличие гистерезиса на изотерме адсорбции. В некоторых случаях гистерезис вызывается кинетическими факторами (смачивание). Капиллярная конденсация описывается уравнением Кельвина, в которое входит радиус кривизны мениска. Это позволяет рассчитывать функции распределения пор по размерам. В принципе количественная характеристика дисперсных систем по дисперсности может быть представлена распределением массы, объема, размером частиц по радиусу поверхности. Метод расчета функции распределения частиц (пор) по размерам заключается в построении интегральных и дифференциальных кривых распределения. Для простых тел наиболее типичными является распределение пор по радиусу. Поэтому интегральная кривая распределения выражает зависимость общего объема пор от их радиуса: Vn=f(r). Из кривой (рис. 2.3.2.3, а) видно, что общий объем малых пор относительно небольшой. Однако доля поверхности, приходящаяся на эти поры, существенно велика. С увеличением размера пор объем увеличивается быстрее, чем поверхность. Построение разных кривых распределения позволяет более правильно представить структуру пористого тела.
Размеры микропор соизмеримы с размерами адсорбированных молекул. В отличие от Ленгмюровского микрослоя в микропорах молекулы расположены в основном вдоль поры и взаимодействуют друг с другом подобно взаимодействию с полимолекулярными слоями преобразования. Но в отличие от последнего большинство молекул находится в непосредственном контакте со стенками пор. Поэтому ни теория БЭТ, ни теория Ленгмюра для процесса адсорбции микропористыми телами неприемлемы. Закономерности заполнения микропор также нельзя описать теорией капиллярной конденсации. Это объясняется перекрыванием полей поверхностных сил в противоположных стенках, что значительно увеличивает энергию адсорбции. Гистерезис в микропорах обычно не наблюдается. Особенность адсорбции на микропористых телах проявляется в их избирательном действии. Это происходит благодаря тому, что большинство адсорбированных молекул взаимодействует непосредственно с поверхностью. Кроме этого у микропор наблюдается так называемый ситовый эффект. Суть его в том, что адсорбируются только те молекулы, размер которых меньше или равен радиусу пор. Поэтому микропористые адсорбенты часто называют молекулярными ситами. В основе количественных соотношений теории объемного заполнения пор лежит теория Поляни. Утверждается следующее. 1. В адсорбционном пространстве действуют только дисперсионные силы, которые аддитивны и не зависят от температуры. Т.е. при адсорбции характер взаимодействия между молекулами адсорбата не изменяется, а происходит только увеличение концентрации на поверхности адсорбента. 2. Активных центров нет, а есть непрерывное силовое поле. 3. Адсорбционные силы действуют на расстоянии большем, чем монослой адсорбата, поэтому говорят об абсорбционном объеме, который заполняется жидким адсорбатом. 4. Действие адсорбционных сил уменьшается по мере удаления от адсорбента и на каком-то расстоянии они равны нулю. 5. Притяжение данной молекулы поверхностного адсорбента не зависит от наличия в адсорбционнои пространстве других молекул, вследствие этого возможна полимолекулярная адсорбция. 6. Адсорбционные силы не зависят от температуры. И, следовательно, с изменением температуры адсорбционный объем не изменяется. Это не противоречит тому, что с увеличением температуры адсорбция уменьшается, а свидетельствует о том, что в результате нагревания и увеличения интенсивности теплового движения адсорбированных молекул увеличивается десорбция. На рис. 2.3.2.4 показан разрез адсорбционного объема. Как во всяком поле, в них можно представить эквипотенциальные поверхности, т.е. поверхности, где адсорбционный потенциал постоянен - это пунктирные линии.
Под адсорбционным потенциалом e следует понимать работу, совершаемую против адсорбционных сил при перемещении одного моля газа с поверхности жидкого адсорбата (рs) в газовую фазу (р). В теории Поляни сделано допущение, что практически все адсорбированное вещество находится в жидком состоянии. Это позволяет заменить зависимость адсорбционного потенциала от расстояния (которое для пористого адсорбента определить невозможно) на функцию объемного жидкого адсорбента. Этот объем можно определить из экспериментально полученной изотермы адсорбции (рис. 2.3.2.5), дающей величину адсорбции:
V = AVm, где V - адсорбционный объем, заполненный жидкостью; А - величина адсорбции, моль; Vm - мольный объем адсорбата.
т.е. адсорбционный потенциал при постоянном объеме не зависит от температуры. Это так называемая температурная инвариантность. Для двух разных температур можно записать: V=A1VМ1=A2VМ2;
Эти соотношения показывают, что, зная изотерму при одной температуре, можно рассчитать изотерму при другой температуре. В дальнейшем теорию Поляни разработал М.М. Дубинин. Так, им обнаружено важное свойство, характерное для потенциальных кривых адсорбции: характеристические кривые для одного и того же адсорбента и разных адсорбатов при всех значениях объемов адсорбата в поверхностном слое находятся в постоянном соотношении b, т.е. (e/e0)V = b - коэффициент аффинности, где e0 – адсорбционный потенциал для адсорбата, выбранного за стандарт. Используя теорию Поляни и обобщив экспериментальный материал, Дубинин пришел к выводу о возможности применения функции распределения Вейбулла Q =f (V) в качестве функции распределения адсорбционного объема по значению потенциала для описания адсорбции на микропористых адсорбентах. Применительно к распределению степени заполнения по адсорбционному потенциалу функцию распределения Вейбулла представляют соотношением q = f(C). Это выражается следующим образом:
где E, n - параметры, не зависящие от температуры; e - адсорбционный потенциал; Е характеристическая энергия адсорбции. Отношение
характеристических энергий для двух адсорбатов также равно
В логарифмическом виде они имеют линейную форму:
Адсорбционные равновесия
Адсорбционное равновесие в системе "газ – жидкость". Закон Генри. Мономолекулярная адсорбция в системах "газ – жидкость", "жидкость – жидкость", "газ – твердое". Изотерма адсорбции Ленгмюра. Уравнение Фрейндлиха. Теория полимолекулярной адсорбции БЭТ. Уравнение БЭТ Предположим, что имеются компоненты-неэлектролиты. Будем считать, что адсорбат образует на поверхности адсорбента мономолекулярный слой. Мономолекулярная адсорбция с точки зрения термодинамики процесса выражается химическим потенциалом в адсорбционном слое и объемной фазе:
где
При равновесии
потенциалы равны: Преобразуем:
Выражение А=а×Кг закон Генри, т.е. при разбавлении системы коэффициент распределения стремится к постоянному значению, равному константе Генри. Если концентрация в сорбционном слое стремится к нулю, то а » с; а = ×с; à 1. Поэтому на практике закон Генри используют в следующем виде: а=Кгсi. Если одна из фаз – газ, то имеем следующий вид: a = КгРi, Кг = Кг/RT.
Эти уравнения представляют собой уравнения изотермы адсорбции при малых концентрациях. В соответствии с этими уравнениями можно по другому сформулировать закон Генри: величина адсорбции при малых давлениях газа (малых концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации). Эти зависимости показаны на рисунке 2.3.1.1. При адсорбции на твердых телах область действия закона мала из-за неоднородности поверхности, но даже на однородной поверхности при увеличении концентрации обнаруживается отклонение от закона. При малых концентрациях распределенного вещества отклонения обусловлены в основном соотношением между взаимодействием молекул друг с другом и с поверхностью адсорбента. Если когезионные взаимодействия адсорбата больше, то отклонение от закона отрицательно и <1, и коэффициент распределения увеличивается (кривая 1 на рис. 2.3.1.1). Если сильнее взаимодействие "адсорбат – адсорбент", то отклонение положительно и D уменьшается (кривая 2 на рис. 2.3.1.1). При дальнейшем увеличении концентрации происходит уменьшение свободной поверхности, снижается реакционная способность и кривые загибаются к оси абсцисс. Константу Генри получают экстраполяцией коэффициента распределения на нулевую концентрацию. В соответствии с правилом фаз Гиббса в гетерогенных системах равновесные параметры зависят от дисперсности или удельной поверхности. Для адсорбционных систем эта зависимость выражается в уменьшенных концентрациях вещества в объемной фазе с увеличением удельной поверхности адсорбента. Если в такой системе содержание распределяемого вещества постоянно, то АmSуд + сV = const, где m - масса адсорбента; Sуд- удельная поверхность адсорбента; V - объем фазы, из которой извлекается вещество; const постоянное количество вещества в системе.
D - коэффициент распределения;
Из соотношения следует, что с увеличением удельной поверхности при постоянной концентрации адсорбата концентрация уменьшается и тем сильнее, чем больше константа Генри и меньше объем фазы. Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями. 1. Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента - образуется мономолекулярный слой. 2. Адсорбционные центры энергетически эквивалентны - поверхность адсорбента эквипотенциальна. 3. Адсорбированные молекулы не взаимодействуют друг с другом. Ленгмюр предположил, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
где А - адсорбционые центры поверхности; В - распределенное вещество; АВ - образующийся комплекс на поверхности. Константа равновесия
процесса: где сав = А - величина адсорбции; са = А0 = А¥ - А, где А¥ - емкость адсорбционного монослоя или число адсорбционных центров, приходящихся на единицу поверхности или единицу массы адсорбента; А0 - число оставшихся свободных адсорбционных центров, приходящихся на единицу площади или единицу массы адсорбента; св – концентрация распределенного вещества. Подставляя величину концентрации в уравнение константы, получим выражения
А = А¥Кс
АКс,
Эти выражения уравнения изотермы адсорбции Ленгмюра. К и Кр в уравнении характеризуют энергию взаимодействия адсорбента с адсорбатом. Адсорбционное уравнение часто представляют относительно степени заполнения поверхности, т.е. как отношение А/А¥:
Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения, записанного в линейной форме;
Такая линейная зависимость позволяет графически определить А¥ и К. Зная А¥, можно определить удельную поверхность адсорбента (поверхность единицы массы адсорбента):
где А¥ - предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента; NA число Авогадро; w0 площадь, занимаемая одной молекулой адсорбата. 1. Если сà 0, тогда уравнение примет вид: А=А¥Кс;
т.е. при сà 0 уравнение Ленгмюра переходит в уравнение Генри. 2. Если сà¥, тогда А = А¥ , А/А¥ = 1. Это случай предельной адсорбции. 3. Пусть адсорбция идет из смеси компонентов, в этом случае уравнение Ленгмюра записывается следующим образом:
Все рассмотренные выше уравнения справедливы для мономолекулярной адсорбции на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности этим свойством не обладают. Приближенной к реальности является возможность распределения адсорбционных центров по энергии. Приняв линейное распределение, Темкин использовал формулу уравнения Ленгмюра и получил уравнение для средних степеней заполнения адсорбента.
где - константа, характеризующая линейное распределение; К0 - константа уравнения Ленгмюра, отвечающая максимальной теплоте адсорбции. Из уравнения следует, что увеличение парциального давления (из-за увеличения концентрации) одного компонента подавляет адсорбцию другого и тем сильнее, чем больше его адсорбционная константа равновесия. Уравнение часто называют логарифмической изотермой адсорбции. Если принять экспоненциальное распределение центров по поверхности, то в области средних заполнений получается ранее найденное эмпирическим путем уравнение Фрейндлиха:
Прологарифмировав,
получим где K, n – постоянные. Использование уравнения Фрейндлиха в логарифмической форме позволяет определить константу уравнения. Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.
В результате этих представлений была выведена следующая формула:
где KL = aж/ап константа конденсации пара; аж - активность вещества в жидкости; ап - активность вещества в состоянии насыщенного пара; ап = Рs. Физический смысл С: характеризует разность энергии Гиббса в процессах чистой адсорбции и конденсации. Это уравнение получило название БЭТ (Бранауэр-Эммет- Теллер). При р/рs<<1, уравнение БЭТ превращается в уравнение Легмюра, которое при дальнейшем уменьшении давления (Рà 0) переходит в закон Генри:
При обработке экспериментальных данных уравнение БЭТ используют в линейной форме (рис. 2.3.1.4):
таким образом графически находят обе константы уравнения А¥ и С. |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


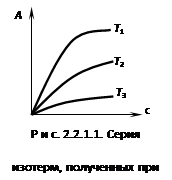




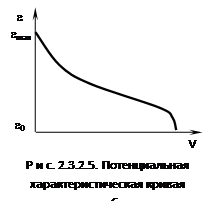
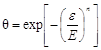 ,
,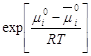 -
константа Генри. Она не зависит от концентрации, определяется при постоянной
температуре, A/a=Kг,
-
константа Генри. Она не зависит от концентрации, определяется при постоянной
температуре, A/a=Kг,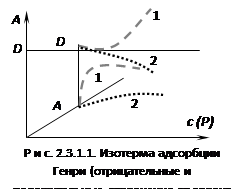
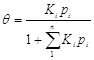 .
. Однако в большинстве случаев
мономолекулярный адсорбционный слой не компенсирует полностью избыточную
поверхностную энергию и поэтому остается возможность влияния поверхностных сил
на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и
пары адсорбируются при температуре ниже критической, т.е. образуются
полимолекулярные слои на поверхности адсорбента, что можно представить как
вынужденную конденсацию (рис. 2.3.1.2 и 2.3.1.3).
Однако в большинстве случаев
мономолекулярный адсорбционный слой не компенсирует полностью избыточную
поверхностную энергию и поэтому остается возможность влияния поверхностных сил
на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и
пары адсорбируются при температуре ниже критической, т.е. образуются
полимолекулярные слои на поверхности адсорбента, что можно представить как
вынужденную конденсацию (рис. 2.3.1.2 и 2.3.1.3).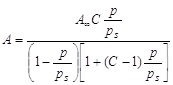 -
уравнение полимолекулярной адсорбции БЭТ,
-
уравнение полимолекулярной адсорбции БЭТ,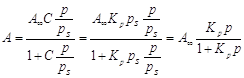 .
.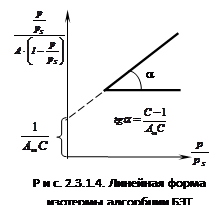
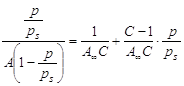 ;
;