|
Реферат: Адсорбция и адсорбционные равновесияРеферат: Адсорбция и адсорбционные равновесияАдсорбция
Понятие адсорбции. Автоадсорбция. Адсорбент и адсорбат. Абсолютная и Гиббсовская адсорбция. Единицы измерения адсорбции. Зависимость величины адсорбции от концентрации, давления и температуры. Изотерма, изобара, изопикна, изостера адсорбции Адсорбция - процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы. Адсорбция может наблюдаться в многокомпонентных системах и при перераспределении в поверхностный слой уходит тот компонент, который сильнее понижает поверхностное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры - уплотнение, которое называется автоадсорбцией. В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению, но и за счет химической реакции компонентов с поверхностью вещества. В этом случае поверхностная энергия может даже увеличиваться на фоне снижения энергии всей системы. Вещество, на поверхности которого происходит адсорбция, называется адсорбентом, а вещество, которое перераспределяется – адсорбатом. Обратный процесс перехода вещества с поверхности в объем фазы - десорбция. В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело жидкость, жидкость - жидкость, жидкость - газ. Для количественного описания адсорбции применяют две величины: первая измеряется числом молей или граммами, приходящимися на единицу поверхности или массы адсорбента: А = m1/m2 - абсолютная адсорбция, А = ni/S. Величина, определяемая избытком вещества в поверхностном слое, также отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или относительной адсорбцией (Г).
Адсорбция зависит от концентрации компонентов и температуры. А = f(c,T)- жидкость; А = f(P,T)- газ Различают следующие виды зависимостей:
Фундаментальное уравнение Гиббса. Определение Гиббсовской адсорбции. Адсорбционное уравнение ГиббсаСчитаем Vповерхности раздела = 0. dU
= TdS +s
dS + Проинтегрировав, получим: U = TS + sS + Полный дифференциал от этого уравнения: dU
= TdS + SdT + sdS + Подставляя значение dU из (6) в (7) и сократив одинаковые члены правой и левой части, получим: SdT
+ Sds + Предположим, что T
= const: Разделив правую и левую часть на поверхность S, получим фундаментальное адсорбционное уравнение Гиббса:
Определение зависимости поверхностного натяжения от адсорбции одного компонента, при постоянстве химических потенциалов других компонентов.
Известно, что
Активность связана с концентрацией: с = ×а. Предположим, что = 1 (при с ® 0). Тогда
Обычно уравнение Гиббса применяют для растворов. Растворителем может быть не только индивидуальное вещество, но и смесь. В разбавленных растворах гиббсовская адсорбция очень мала, а его химический потенциал меняется очень мало с изменением концентрации растворенного вещества, т.е. dm= 0. Поэтому для разбавленного раствора фундаментальное уравнение Гиббса выглядит так:
Из этих уравнений
следует, что зная зависимость Зная эти производные уравнения Гиббса, можно рассчитать значение Г, что позволяет построить зависимость Г = f(С). Уравнение Гиббса показывает, что единица измерения гиббсовской адсорбции не зависит от единицы измерений концентрации, а зависит от размерности величины R. Так как величина R отнесена к молю вещества, а s - к единице площади, то Г = [моль/ единица площади]. Если s выразить в [Дж/м2], то R нужно подставлять: R = 8,314 Дж/моль×К. Поверхностная активность. Поверхностно-активные и поверхностно-инактивные вещества. Анализ уравнения Гиббса. ПАВ. Эффект Ребиндера. Правило Дюкло-ТраубеВ уравнении Гиббса
влияние природы вещества на адсорбцию отражается производной
g = [Дж×м/моль] = [Н×м2/моль]; [эрг см/моль] = [Гиббс]. Уравнение показывает,
что чем сильнее снижается Физический смысл поверхностной активности состоит в том, что она представляет силу, удерживающую вещество на поверхности и отнесенную к единице гиббсовской адсорбции. Поверхностную активность можно представить как отрицательный тангенс угла наклона к касательной, проведенной к кривой Г = f(C) в точке пересечения с осью ординат. Поверхностная активность может быть положительной и отрицательной. Значение и знак ее зависят от природы растворенного вещества и растворителя. 1. 1.
2. g = 0, Г = 0 - адсорбции нет, т.е. вещество индифферентно. Поверхностно-активными веществами являются органические вещества, состоящие из углеводородного радикала и функциональной группы. Неорганические соли являются поверхностно-инактивными веществами. Ребиндер и Щукин в своих работах показали, что развитие микротрещин в твердых телах при деформации может происходить гораздо легче при адсорбции веществ из среды, в которой ведется деформирование: адсорбироваться могут как ионы электролитов, так и молекулы поверхностно-активного вещества (ПАВ), образуя на адсорбирующей поверхности их двумерный газ в результате нелокализованной адсорбции. Молекулы под давлением этого газа проникают в устье трещин и стремятся раздвинуть их, таким образом содействуя внешним силам, т.е. наблюдается адсорбционное понижение твердости твердого тела, что получило название эффекта Ребиндера. Поверхностная активность в гомологическом ряду поверхностно-активных веществ (ПАВ) повышается в среднем в 3,2 раза на каждую группу СН2 (в водных растворах)– правило Дюкло – Траубе. Адсорбционные равновесия
Адсорбционное равновесие в системе «газ – жидкость». Закон Генри. Мономолекулярная адсорбция в системах «газ – жидкость», «жидкость – жидкость», «газ – твердое». Изотерма адсорбции Ленгмюра. Уравнение Фрейндлиха. Теория полимолекулярной адсорбции БЭТ. Уравнение БЭТ Предположим, что имеются компоненты-неэлектролиты. Будем считать, что адсорбат образует на поверхности адсорбента мономолекулярный слой. Мономолекулярная адсорбция с точки зрения термодинамики процесса выражается химическим потенциалом в адсорбционном слое и объемной фазе:
где
При равновесии
потенциалы равны: Преобразуем:
Выражение А=а×Кг закон Генри, т.е. при разбавлении системы коэффициент распределения стремится к постоянному значению, равному константе Генри. Если концентрация в сорбционном слое стремится к нулю, то а » с; а = ×с; à 1. Поэтому на практике закон Генри используют в следующем виде: а=Кгсi. Если одна из фаз – газ, то имеем следующий вид: a = КгРi, Кг = Кг/RT.
Эти уравнения представляют собой уравнения изотермы адсорбции при малых концентрациях. В соответствии с этими уравнениями можно по другому сформулировать закон Генри: величина адсорбции при малых давлениях газа (малых концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации). Эти зависимости показаны на рисунке 2.3.1.1. При адсорбции на твердых телах область действия закона мала из-за неоднородности поверхности, но даже на однородной поверхности при увеличении концентрации обнаруживается отклонение от закона. При малых концентрациях распределенного вещества отклонения обусловлены в основном соотношением между взаимодействием молекул друг с другом и с поверхностью адсорбента. Если когезионные взаимодействия адсорбата больше, то отклонение от закона отрицательно и <1, и коэффициент распределения увеличивается (кривая 1 на рис. 2.3.1.1). Если сильнее взаимодействие «адсорбат – адсорбент», то отклонение положительно и D уменьшается (кривая 2 на рис. 2.3.1.1). При дальнейшем увеличении концентрации происходит уменьшение свободной поверхности, снижается реакционная способность и кривые загибаются к оси абсцисс. Константу Генри получают экстраполяцией коэффициента распределения на нулевую концентрацию. В соответствии с правилом фаз Гиббса в гетерогенных системах равновесные параметры зависят от дисперсности или удельной поверхности. Для адсорбционных систем эта зависимость выражается в уменьшенных концентрациях вещества в объемной фазе с увеличением удельной поверхности адсорбента. Если в такой системе содержание распределяемого вещества постоянно, то АmSуд + сV = const, где m - масса адсорбента; Sуд- удельная поверхность адсорбента; V - объем фазы, из которой извлекается вещество; const постоянное количество вещества в системе.
D - коэффициент распределения;
Из соотношения следует, что с увеличением удельной поверхности при постоянной концентрации адсорбата концентрация уменьшается и тем сильнее, чем больше константа Генри и меньше объем фазы. Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями. 1. Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента - образуется мономолекулярный слой. 2. Адсорбционные центры энергетически эквивалентны - поверхность адсорбента эквипотенциальна. 3. Адсорбированные молекулы не взаимодействуют друг с другом. Ленгмюр предположил, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
АВ - образующийся комплекс на поверхности. Константа равновесия
процесса: где сав = А - величина адсорбции; са = А0 = А¥ - А, где А¥ - емкость адсорбционного монослоя или число адсорбционных центров, приходящихся на единицу поверхности или единицу массы адсорбента; А0 - число оставшихся свободных адсорбционных центров, приходящихся на единицу площади или единицу массы адсорбента; св – концентрация распределенного вещества. Подставляя величину концентрации в уравнение константы, получим выражения
А = А¥Кс
АКс,
Эти выражения уравнения изотермы адсорбции Ленгмюра. К и Кр в уравнении характеризуют энергию взаимодействия адсорбента с адсорбатом. Адсорбционное уравнение часто представляют относительно степени заполнения поверхности, т.е. как отношение А/А¥:
Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения, записанного в линейной форме;
Такая линейная зависимость позволяет графически определить А¥ и К. Зная А¥, можно определить удельную поверхность адсорбента (поверхность единицы массы адсорбента):
где А¥ - предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента; NA число Авогадро; w0 площадь, занимаемая одной молекулой адсорбата. 1. Если сà 0, тогда уравнение примет вид: А=А¥Кс;
т.е. при сà 0 уравнение Ленгмюра переходит в уравнение Генри. 2. Если сà¥, тогда А = А¥ , А/А¥ = 1. Это случай предельной адсорбции. 3. Пусть адсорбция идет из смеси компонентов, в этом случае уравнение Ленгмюра записывается следующим образом:
Все рассмотренные выше уравнения справедливы для мономолекулярной адсорбции на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности этим свойством не обладают. Приближенной к реальности является возможность распределения адсорбционных центров по энергии. Приняв линейное распределение, Темкин использовал формулу уравнения Ленгмюра и получил уравнение для средних степеней заполнения адсорбента.
где - константа, характеризующая линейное распределение; К0 - константа уравнения Ленгмюра, отвечающая максимальной теплоте адсорбции. Из уравнения следует, что увеличение парциального давления (из-за увеличения концентрации) одного компонента подавляет адсорбцию другого и тем сильнее, чем больше его адсорбционная константа равновесия. Уравнение часто называют логарифмической изотермой адсорбции. Если принять экспоненциальное распределение центров по поверхности, то в области средних заполнений получается ранее найденное эмпирическим путем уравнение Фрейндлиха:
Прологарифмировав,
получим где K, n – постоянные. Использование уравнения Фрейндлиха в логарифмической форме позволяет определить константу уравнения. Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической. Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию (рис. 2.3.1.2 и 2.3.1.3).
В результате этих представлений была выведена следующая формула:
где KL = aж/ап константа конденсации пара; аж - активность вещества в жидкости; ап - активность вещества в состоянии насыщенного пара; ап = Рs. Физический смысл С: характеризует разность энергии Гиббса в процессах чистой адсорбции и конденсации. Это уравнение получило название БЭТ (Бранауэр-Эммет- Теллер). При р/рs<<1, уравнение БЭТ превращается в уравнение Легмюра, которое при дальнейшем уменьшении давления (Рà 0) переходит в закон Генри:
При обработке экспериментальных данных уравнение БЭТ используют в линейной форме (рис. 2.3.1.4):
таким образом графически находят обе константы уравнения А¥ и С. |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |


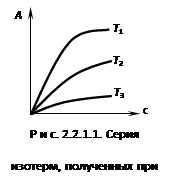
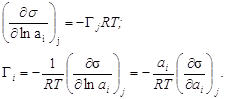
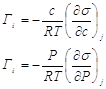 - для жидкости
и газа
- для жидкости
и газа 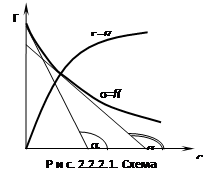
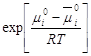 - константа Генри. Она не
зависит от концентрации, определяется при постоянной температуре, A/a=Kг,
- константа Генри. Она не
зависит от концентрации, определяется при постоянной температуре, A/a=Kг,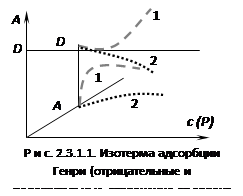
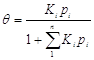 .
.
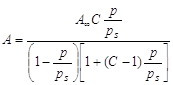 - уравнение
полимолекулярной адсорбции БЭТ,
- уравнение
полимолекулярной адсорбции БЭТ,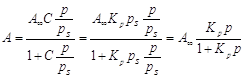 .
.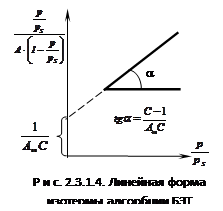
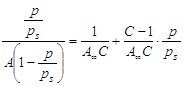 ;
;